【仕事算の解き方】基礎から応用まで問題を使ってイチから解説するぞ！

今回は「仕事算」という計算方法について解説していきます。

中学受験で出題されるほか、就職試験に活用されるSPIなどでもよく目にする問題です。

問題は非常にシンプル！

だけど、どうやって解けばいいのかわかんない…

それが仕事算の難しさ(^^;)

でもね、ポイントを押さえておけば楽勝で解けるようになります★

ってことで、仕事算の解き方・考え方をイチから学習していきましょー！！

仕事算の解き方

これが仕事算の問題です。

この問題を解くためには、2つの考え方があります。

全体を1とする

仕事全体を1として考える。

これが仕事算の一般的な解き方になります。

Aは15日間で仕事を完成させることができます。

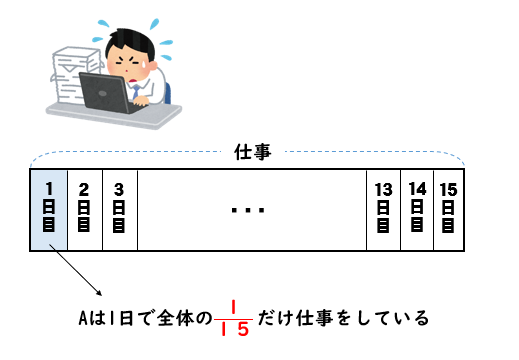
なので、Aは1日に\(\displaystyle{\frac{1}{15}}\) だけ仕事をしているということになります。

Bも同様に考えると、\(\displaystyle{\frac{1}{10}}\) だけ仕事をしています。

すると、2人が一緒に仕事をするとどうなるでしょうか。

2人の仕事パワーが合わさって

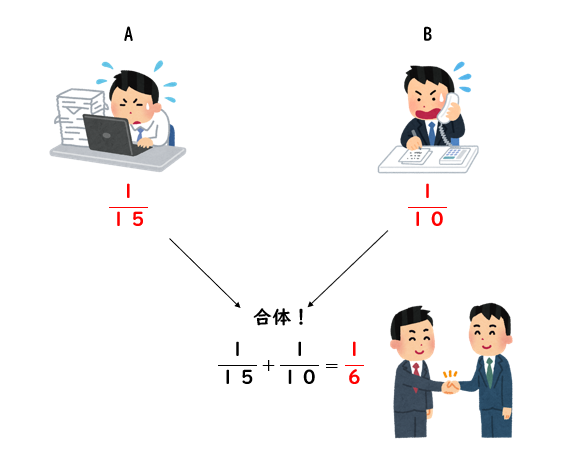
1日にできる仕事量は\(\displaystyle{\frac{1}{15}+\frac{1}{10}=\frac{1}{6}}\) となります。

分母が違う分数の足し算だから通分して計算してね！

$$\begin{eqnarray}\frac{1}{15} +\frac{1}{10}&=&\frac{2}{30}+\frac{3}{30}\\[5pt]&=&\frac{5}{30}\\[5pt]&=&\frac{1}{6}\end{eqnarray}$$

仕事全体を1として考えているので、2人で仕事をする場合には

$$1\div \frac{1}{6}=1\times \frac{6}{1}=6$$

以上より、6日間で仕事が完成すると分かりました。

簡単ですね！

まずは、AとBが1日にどれくらいの仕事をするか求める。

それらを合体させることで2人で仕事した場合の仕事量を求める。

最後に1÷（2人の仕事量）を計算すればOK！

最小公倍数を考える

次は、仕事全体を最小公倍数に設定するというやり方です。

今回の問題ではAが15日、Bが10日ということから、15と10の最小公倍数である30を仕事全体の数として考えていきます。

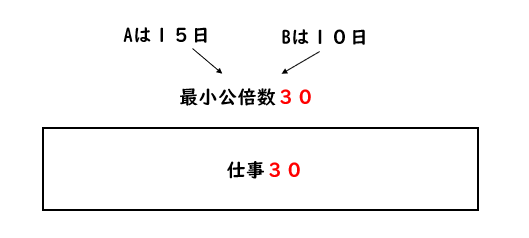
仕事全体を30とすると、Aが1日でできる仕事量は \(30\div15=\color{red}{2}\) となります。

同様にBが1日できる仕事量は \(30\div10=\color{red}{3}\) です。

すると、2人が一緒に仕事をすると1日にできる仕事量は \(2+3=\color{red}{5}\) となりますね。

いま、仕事全体を30として考えているので、1日に5の仕事をこなしていくのであれば

$$30\div 5=6$$

つまり、6日間で仕事を完成させることができるとわかります。

これが最小公倍数を使った考え方です！

とってもシンプルで簡単でしたね(^^)

全体を1として分数を使って解いていくのが一般的ではありますが、状況によっては最小公倍数を使うなどして計算をラクにやっていきたいですね！

では、次の章からは実践です。

いろんな仕事算の問題を紹介していきますので、それぞれの解き方について理解を深めていきましょう。

仕事算の基礎問題の解き方

Bが1人では何日？？

仕事全体を1として考えると

Aが1日にできる仕事量は\(\displaystyle{\frac{1}{10}}\)

AとBが2人で仕事をする場合、1日にできる仕事量は\(\displaystyle{\frac{1}{6}}\) と表すことができます。

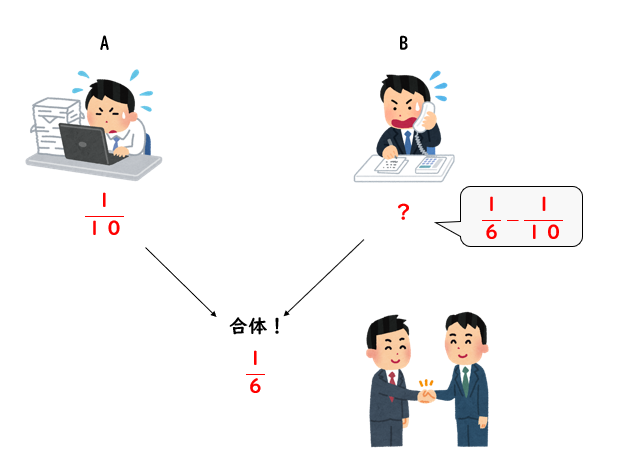
すると、Bが1日にできる仕事量は、2人の仕事量からAの仕事量を引いてあげれば求めれますね。

$$\frac{1}{6}-\frac{1}{10}=\frac{10}{60}-\frac{6}{60}=\frac{1}{15}$$

以上より、Bは1日に\(\displaystyle{\frac{1}{15}}\) だけ仕事をこなすことができるので

$$1\div \frac{1}{15}=1\times \frac{15}{1}=15$$

Bが1人で仕事をした場合には、15日間かかるということが分かりました。

残りはBがやると何日かかる？

仕事全体を1として考えると

Aが1日でできる仕事量は \(\displaystyle{\frac{1}{12}}\)

Bが1日でできる仕事量は \(\displaystyle{\frac{1}{15}}\) と表すことができます。

まず、Aが4日間仕事をすると

$$\frac{1}{12}\times 4=\frac{1}{3}$$

これだけ仕事をしたことになります。

すると、残りの仕事量は

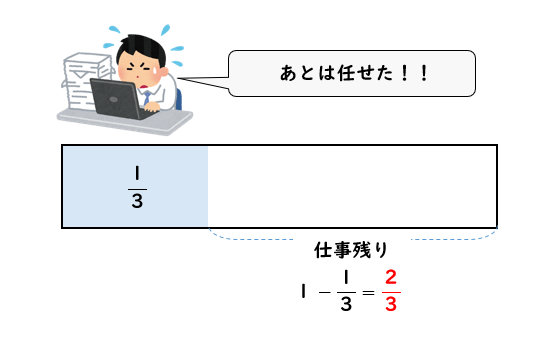
$$1-\frac{1}{3}=\frac{3}{3}-\frac{1}{3}=\frac{2}{3}$$

となります。

残りの仕事量をBがこなしていくと

$$\frac{2}{3}\div \frac{1}{15}=\frac{2}{3}\times \frac{15}{1}=10$$

10日間かかるということが分かります。

よって、この仕事はAが4日間、Bが10日間かけて完成するので合計で14日間かかるということになります。

3人のときは？？

仕事全体を1として考えると

Aが1日でできる仕事量は \(\displaystyle{\frac{1}{6}}\)

Bが1日でできる仕事量は \(\displaystyle{\frac{1}{4}}\)

Cが1日でできる仕事量は \(\displaystyle{\frac{1}{12}}\)

このようにそれぞれ表すことができます。

よって、3人で仕事をする場合の仕事量は

$$\begin{eqnarray} \frac{1}{6}+\frac{1}{4}+\frac{1}{12}&=&\frac{2}{12}+\frac{3}{12}+\frac{1}{12}\\[5pt]&=&\frac{6}{12}\\[5pt]&=&\frac{1}{2}\end{eqnarray}$$

となります。

よって、仕事が完成するまでにかかる日数は

$$1\div \frac{1}{2}=1\times \frac{2}{1}=2$$

2日間ということが分かりました。

3人や4人に人数が増えても考え方は一緒だね(^^)

仕事算の応用問題の解き方

途中から一人でやると何日？？

ちょっとややこしい問題だけど、図で考えてみるとこんな感じ！

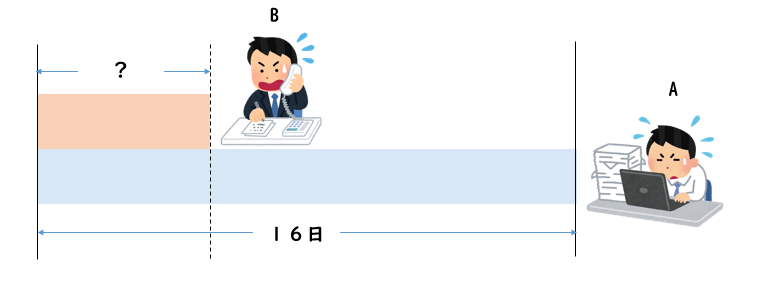
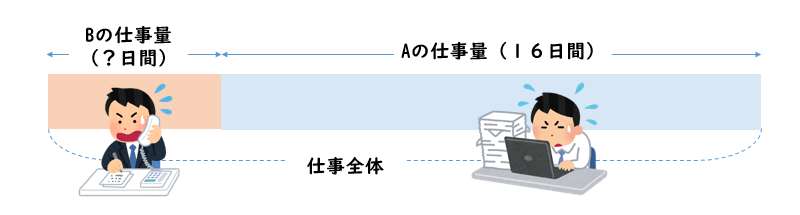
仕事全体から、Aが16日間でこなした仕事の量を引けばBがこなした仕事量を考えることができます。

そこからBが仕事していた日数、つまり2人で仕事していた日数を求めることができます。

仕事全体を1として考えると

Aが1日でできる仕事量は \(\displaystyle{\frac{1}{20}}\)

Bが1日でできる仕事量は \(\displaystyle{\frac{1}{30}}\) と表せます。

Aが16日間の間にこなした仕事量は

$$\frac{1}{20}\times 16=\frac{4}{5}$$

ということから、Bがこなした仕事量は

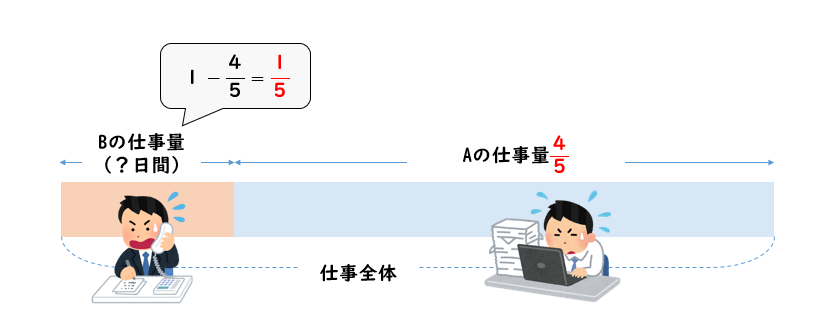
$$1-\frac{4}{5}=\frac{5}{5}-\frac{4}{5}=\frac{1}{5}$$

となります。

よって、Bが仕事していた日数は

$$\frac{1}{5}\div \frac{1}{30}=\frac{1}{5}\times \frac{30}{1}=6$$

6日間ということが分かります。

3人いるときの組み合わせいろいろ

仕事全体を1とすると

AとBの2人で仕事する場合、1日あたりの仕事量は \(\displaystyle{\frac{1}{18}}\)

AとCの2人で仕事する場合、1日あたりの仕事量は \(\displaystyle{\frac{1}{12}}\)

Aが1人で仕事する場合、1日あたりの仕事量は \(\displaystyle{\frac{1}{72}}\)　と表すことができます。

ここで、BとCそれぞれの1日あたりの仕事量を求めます。

Bの仕事量を求めたい場合、AとBの2人分からAの1人分を引いてやります。

$$\frac{1}{18}-\frac{1}{72}=\frac{3}{72}=\frac{1}{24}$$

Cの仕事量を求めたい場合、AとCの2人分からAの1人分を引いてやります。

$$\frac{1}{12}-\frac{1}{72}=\frac{5}{72}$$

すると、ここからBとCが2人で仕事した場合の1日当たりの仕事量を求めることができます。

$$\begin{eqnarray}\frac{1}{24}+\frac{5}{72}=\frac{8}{72}=\frac{1}{9} \end{eqnarray}$$

よって、BとCの2人で仕事するときにかかる日数は

$$1\div \frac{1}{9}=1\times \frac{9}{1}=9$$

9日間かかるということが求まります。

仕事算まとめ！

お疲れ様でした！

仕事算のいろんな問題について解説しましたが、どれもそんなに難しいものではありませんでしたね。

仕事全体を1として解いていく方法、最小公倍数の数を全体として解いていく方法

それぞれの考え方をしっかりと理解していれば、難なく解くことができたはずです(^^)

今回の記事内容が楽勝だったぜ！という方は

ぜひとも、応用問題集に載っているような難問にも挑戦してみてくださいね