【一次関数】面積を求めるやり方は？2等分の式はなに？

今回は一次関数の単元から

グラフ上にある三角形の面積を求める

という問題の解き方について解説していきます。

また、応用編ということで、三角形を2等分する直線の式は？という問題についても一緒に考えていきましょう！

面積を求めるとなると

うわ、難しそう…

テストで出てきたら飛ばすわ…

っていう方も多いと思います(^^;)

だけど、実際にはね

ポイントをおさえておけば楽勝な問題

です！！

ってことで、やっていこうぜ★

今回の記事は、こちらの動画でも解説しています(/・ω・)/

【一次関数】面積を求めるやり方は？

グラフ上にある図形の面積を求めるために

座標を求めることができる

というのが最も大切なポイントになります。

座標を求める方法については

＞【一次関数】座標の求め方は？いろんな座標を求める問題について解説！

こちらの記事で１から解説をしていまず。

一次関数が苦手だ…という方はまずはこちらの記事で復習しておいてください。

それでは、次の問題について解き方を順に確認していきましょう。

【一次関数】面積を求め方の手順

次の図で、△ABCの面積を求めなさい。

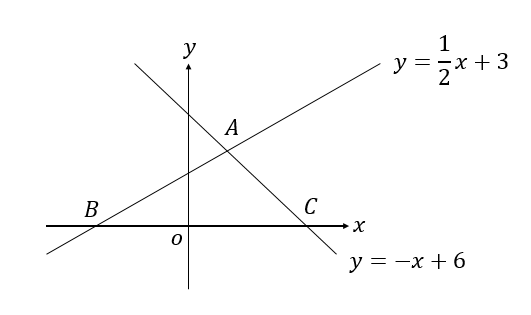
グラフ上にある図形の面積を求めたい場合

まずは、三角形の各頂点の座標を求めます。

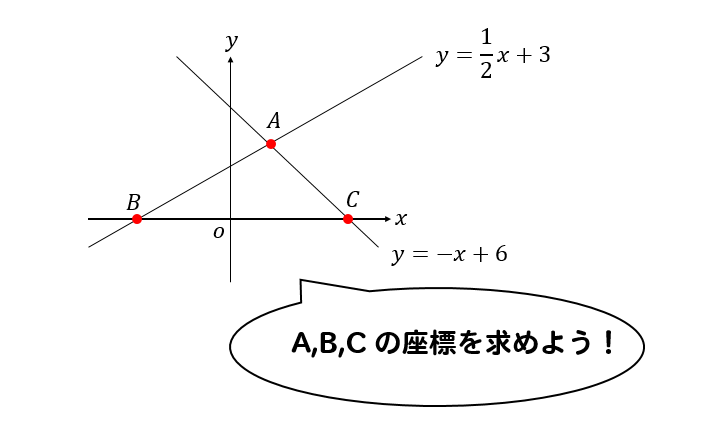
まずは、簡単に求めることができるB,Cの座標からいきましょう。

点Bは\(\displaystyle {y=\frac{1}{2}x+3}\) の\(x\)軸との交点だから

\(\displaystyle {y=\frac{1}{2}x+3}\)に \(y=0\) を代入すると

$$0=\frac{1}{2}x+3\\ \\-\frac{1}{2}x=3\\\\x=-6$$

よって、点Bの座標は\((-6,0)\)と分かります。

点Cは\(\displaystyle {y=-x+6}\) の\(x\)軸との交点だから

\(\displaystyle {y=-x+6}\) に \(y=0\) を代入すると

$$0=-x+6\\ \\x=6$$

よって、点Bの座標は\((6,0)\)と分かります。

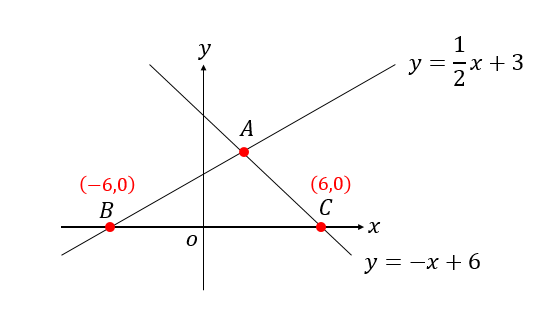
最後に、点Aの座標を求めましょう。

点Aは\(\displaystyle {y=\frac{1}{2}x+3}\)と\(\displaystyle {y=-x+6}\)の交点だから、2つの式から連立方程式で解いていきます。

\begin{eqnarray} \left\{ \begin{array}{l} y=\frac{1}{2}x+3 \\ y=-x+6 \end{array} \right. \end{eqnarray}

\(\displaystyle {y=-x+6}\) を \(\displaystyle {y=\frac{1}{2}x+3}\)に代入すると

$$-x+6=\frac{1}{2}x+3$$

$$-2x+12=x+6$$

$$-3x=-6$$

$$x=2$$

\(x=2\) を \(y=-x+6\)に代入すると

$$y=-2+6=4$$

よって、点Aの座標は\((2,4)\)ということが求まりました。

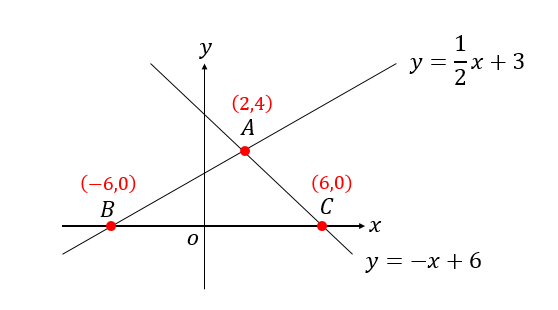
三角形の頂点の座標がすべて求まったら

次はそれを利用して、底辺と高さの大きさを求めていきます。

横の長さであれば、ぞれぞれの\(x\)座標

縦の長さであれば、ぞれぞれの\(y\)座標

を見比べ、次の計算をすることで長さを求めることができます。

$$長さ=座標(大)-座標(小)$$

まずは底辺

BとCの座標を見れば求めることができます。

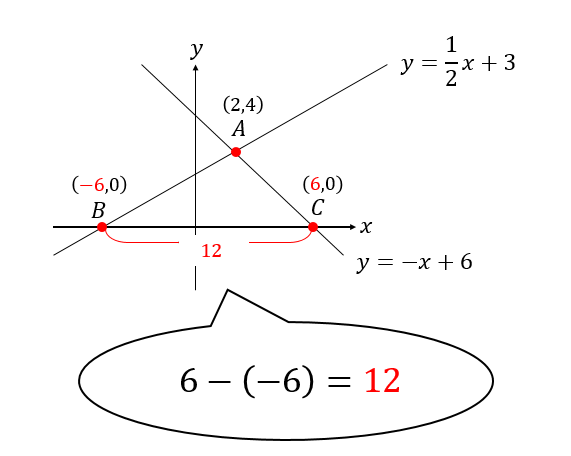
高さの部分は点Aの座標を見ればよいので

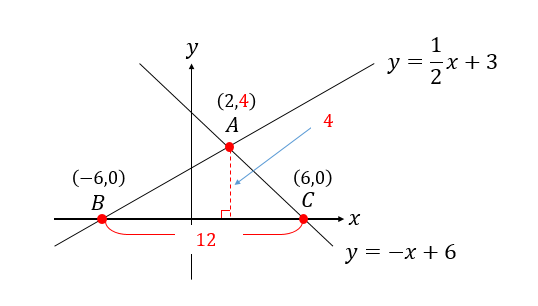
以上より△ABCの底辺は12、高さは4ということが求まったので

$$△ABC=12\times 4\times \frac{1}{2}=\color{red}{24}$$

となりました。

以上の手順をまとめておくとこんな感じ！

多くの人が座標を求めるという１ステップ目でつまづいてしまいます。

ですが、座標を乗り切ったらもうゴールは目の前です。

面積を求めるのが苦手だという方は、まずは座標を求める練習に力を入れてみてはいかがでしょうか。

＞【一次関数】座標の求め方は？いろんな座標を求める問題について解説！

【一次関数】面積を2等分する直線の式は？

それでは、次は発展の問題。

面積を2等分するという問題の解き方を考えてみましょう。

次の図で、点Aを通り△ABCの面積を2等分する直線の式を求めなさい。

点Aを通るように直線を引く場合

△ABCを2等分にしようと思えば

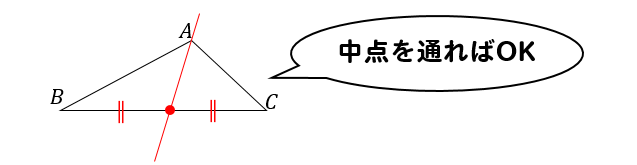
このようにBCの中点を通るように引けば、三角形を2等分することができます。

中点を通るように分割すれば、それぞれの三角形は底辺、高さが等しくなりますよね。

なので、三角形を2等分する直線…という問題であれば、その直線が中点を通るように。と考えてみるとよいです。

では、ここで問題となってくるのは

点Bと点Cの中点ってどこ！？

ってことだよね。

中点の座標を求めるのは簡単！

このように \(x,  y\)座標をそれぞれ足し、2で割る。

これで中点が求めれます。

よって、\(B(-6,0)\) と \(C(6,0)\)の中点は

$$\left(\frac{-6+6}{2},   \frac{0+0}{2}\right)=(0,0)$$

となります。

つまり、点Aを通り△ABCを2等分する直線の式とは

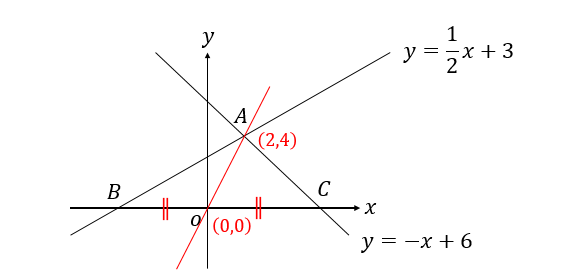
このようにグラフになります。

2点\((2,4), (0,0)\)を通るということより

$$\color{red}{y=2x}$$

となりました。

【一次関数】面積の求め方まとめ！

お疲れ様でした！

グラフ上の面積を求める問題では何といっても

座標を求めるのが大事！！

入試問題になってくると、座標に文字が絡んできたりして複雑になってきます。

だけど、考え方としては今回の記事で紹介した通りです。

文字が出てきても恐れることはなし！

面積を求める手順が理解できたら

いろんな問題を解いて、知識を深めていきましょう！

ファイトだ(/・ω・)/

グラフ上に長さに関する問題については、こちらもご参考ください。

＞【中学関数】グラフから長さを求める方法を基礎から解説！