【数Ⅰ】相関係数の出し方をイチからていねいに解説！

今回の記事では高校数学Ⅰで学習するデータの分析から

「相関係数の出し方」

についてイチから解説していきます。

 

相関係数を出すためには「分散、標準偏差」「共分散」について知っておく必要があります。

ちょっと不安だなぁ…という方はこちらの記事をご参考ください。

 

サクッと理解したい方は、こちらの動画も参考にしてください！

相関係数とはなにか、求め方は？

2つの変量について、どのような関係があるかを調べたいとき

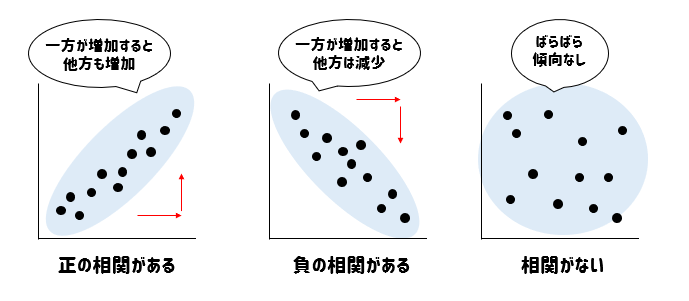
このように散布図を書いて調べることができました。

 

しかし、毎回のように散布図を書いて調べるのはちょっとメンドイですね(^^;)

そこでデータを使って計算をすることによって、どのような相関があるのかを調べましょう！というのが相関係数というものです。

相関係数は次のような計算で求めることができます。

 

相関係数の値は必ず\(-1\)から\(1\)の間となります。

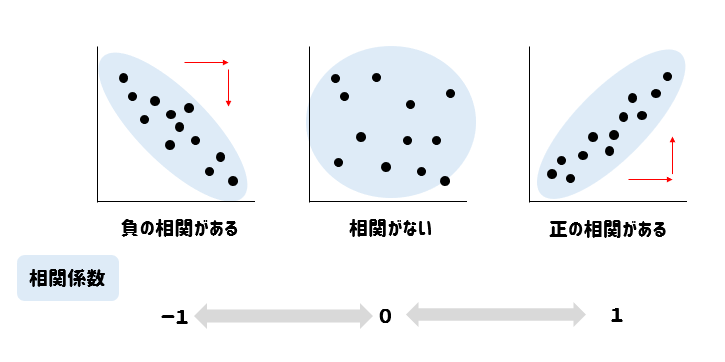
そして、相関係数の値によって、データがどのような相関関係にあるかを読み取ることができます。

 

では、次の章では相関係数の求め方をイチから確認してみましょう。

相関係数の求め方をイチから

相関係数を求めるためには、偏差（平均からどれくらい離れているか）が必要になります。

なので、まずは平均を求めることです。

数学\(x\)、英語\(y\)として話を進めます。

$$\begin{eqnarray}\overline{x}&=&\frac{8+9+6+2+10+3+8+4+9+1}{10}\\[5pt]&=&\frac{60}{10}\\[5pt]&=&6(点) \end{eqnarray}$$

$$\begin{eqnarray}\overline{y}&=&\frac{2+2+5+5+2+5+4+4+4+7}{10}\\[5pt]&=&\frac{40}{10}\\[5pt]&=&4(点) \end{eqnarray}$$

 

そして、平均が求まったら表を使ってそれぞれの偏差を求めましょう。

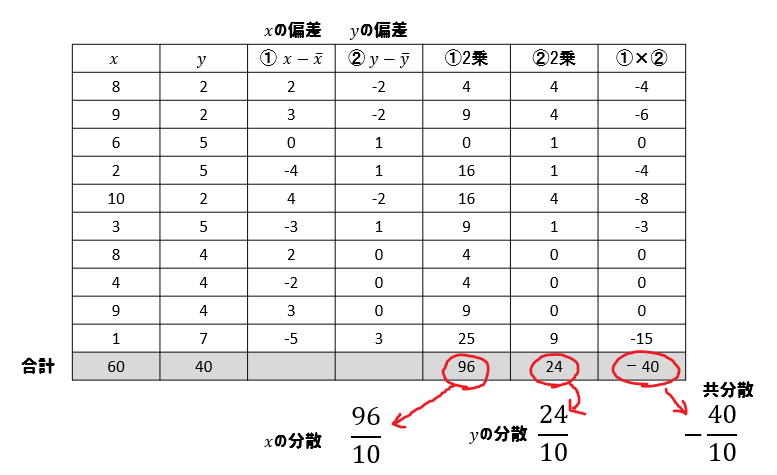
偏差の2乗、偏差の積の部分からそれぞれ分散と共分散を求めましょう。

このとき、あえて割り算はせず分数の形のままにしておきますね。

 

$$標準偏差=\sqrt{分散}$$

ということを思い出してもらって、相関係数の公式にあてはめていくと次のような式ができます。

すると、分母にある10は約分で消えてしまうことが分かりますね。

 

分母の数は毎回消えてしまうので、慣れてきた人は初めから分母を省いてしまってもOKです。

あとは計算あるのみです。

$$\begin{eqnarray}\frac{-40}{\sqrt{96}\times \sqrt{24}}&=&-\frac{40}{4\sqrt{6}\times 2\sqrt{6}}\\[5pt]&=&-\frac{40}{48}\\[5pt]&=&-\frac{5}{6} \\[5pt]&≒& -0.83 \cdots(解)\end{eqnarray}$$

 

相関係数が\(-1\)に近いということから、数学と英語の点数には強い負の相関があるということが分かります。

まとめ！

今回は相関係数の求め方についてまとめておきました。

相関係数の求め方、それが何を表しているのかをしっかりと確認しておいてくださいね。