入試で使える！2変数関数の最大・最小の求め方、パターン別の解説！

高校数学Ⅰで学習する関数の単元から

「2変数関数の最大・最小」

についての問題をパターン別にまとめていきます。

考え方を身につけてしまえば簡単な問題ばかりです。

今回の記事を通して、理解を深めておきましょう。

Contents

条件式付きの2変数関数の最大・最小
条件式なしの2変数関数の最大・最小
まとめ！

条件式付きの2変数関数の最大・最小

条件式が一次

【問題】

$2x+y=4$ のとき，$xy$ の最大値とそのときの $x,y$ の値を求めよ。

一次の条件式が与えられた場合には、それを用いて文字を1つ消去するのが基本的なやり方になります。

$2x+y=4$ ⇒ $y=4-2x$ とし、

これを $xy$ に代入すると

$$\begin{eqnarray}xy&=&x(4-2x)\\[5pt]&=&-2x^2+4x \end{eqnarray}$$

となります。これを平方完成してグラフをかくことによって最大値を求めましょう。

$$\begin{eqnarray}-2x^2+4x&=&-2(x^2-2x)\\[5pt]&=&-2(x-1)^2+2 \end{eqnarray}$$

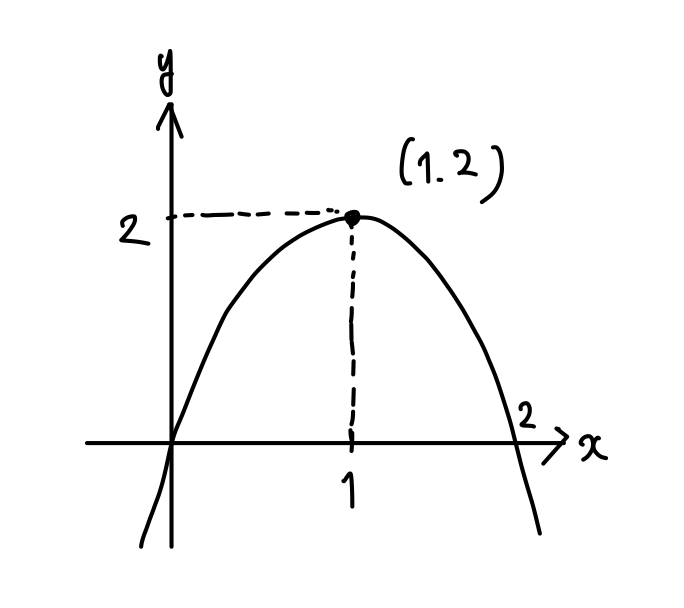
グラフより、$x=1$ のとき最大値$2$

$x=1$ を $y=4-2x$ に代入すると $y=2$ となる。

したがって、

$x=1, y=2$ のとき最大値$2$

ポイント！

条件式を用いて、文字を1つ消去する。

文字が1つになった式を平方完成して、最大最小を求める。

条件式が一次（範囲あり）

【問題】

$x≧0$, $y≧0$, $2x+y=8$ のとき，$xy$ の最大値と最小値を求めよ。

範囲が指定されている場合、消去する文字の条件を残る文字の条件に反映させておくことがポイントです。

文字を消去するために条件式を変形すると

$2x+y=8$ ⇒ $y=-2x+8$ としたとき

$y≧0$ という条件から

$$\begin{eqnarray}y=-2x+8&≧&0\\[5pt]-2x&≧&-8\\[5pt]x&≦&4 \end{eqnarray}$$

$x≧0$ であるから $x$ の範囲は $0≦x≦4$ となります。

このように、消去する$y$ の条件を $x$ に反映して範囲を絞っておくってのがポイントです。

$y=-2x+8$ を $xy$ に代入すると

$$\begin{eqnarray}xy&=&x(-2x+8)\\[5pt]&=&-2x^2+8x\\[5pt]&=&-2(x^2-4x)\\[5pt]&=&-2(x-2)^2+8 \end{eqnarray}$$

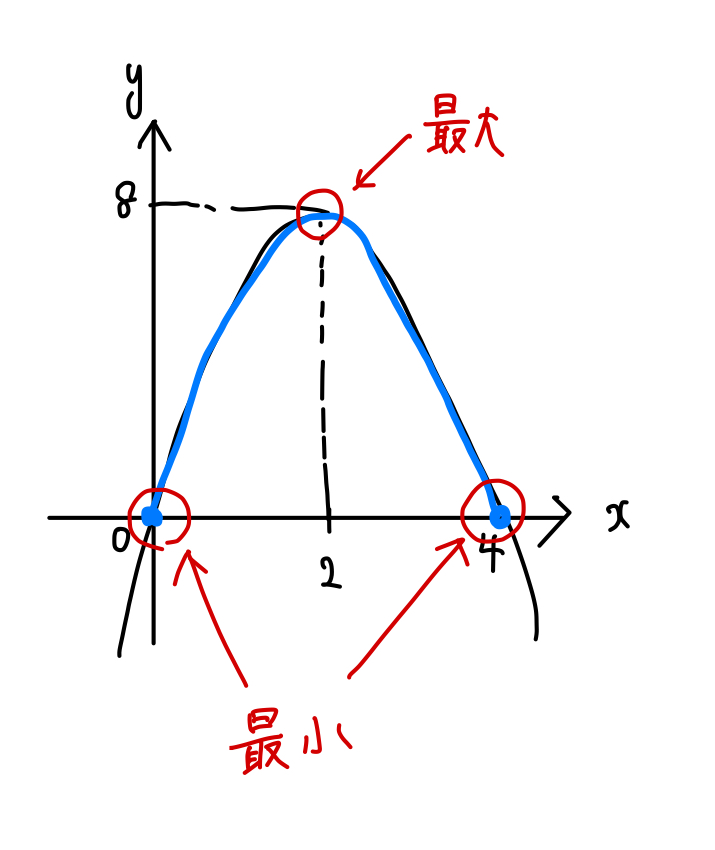
グラフより、$x=2$ のとき最大値$8$

$x=0,4$ のとき最小値$0$ となります。

$x=2$ のとき、$y=-2x+8$ に代入すると $y=4$

$x=0$ のとき、$y=-2x+8$ に代入すると $y=8$

$x=4$ のとき、$y=-2x+8$ に代入すると $y=0$

したがって

$x=2, y=4$ のとき最大値$8$

$x=0, y=8$, $x=4, y=0$ のとき最小値$0$

ポイント！

範囲があるときには、消去する文字の条件を残す文字の条件に反映させておこう！

条件式が二次

【問題】

実数 $x,y$ が $x^2+y^2=1$ をみたすとき，$x^2+4y$ の最大値と最小値を求めよ。

実数条件 $(実数)^2≧0$ を用いて範囲を求めよう！

$x^2+y^2=1$ より $x^2=1-y^2$ となり

$x^2≧0$ となるので、

$$\begin{eqnarray}x^2=1-y^2&≧&0\\[5pt]-y^2&≧&-1\\[5pt]y^2&≦&1\\[5pt]-1≦y&≦&1 \end{eqnarray}$$

$x^2=1-y^2$ を $x^2+y^2=1$ に代入すると

$$\begin{eqnarray}x^2+4y&=&(1-y^2)+4y\\[5pt]&=&-y^2+4y+1\\[5pt]&=&-(y^2-4y)+1\\[5pt]&=&-(y-2)^2+5 \end{eqnarray}$$

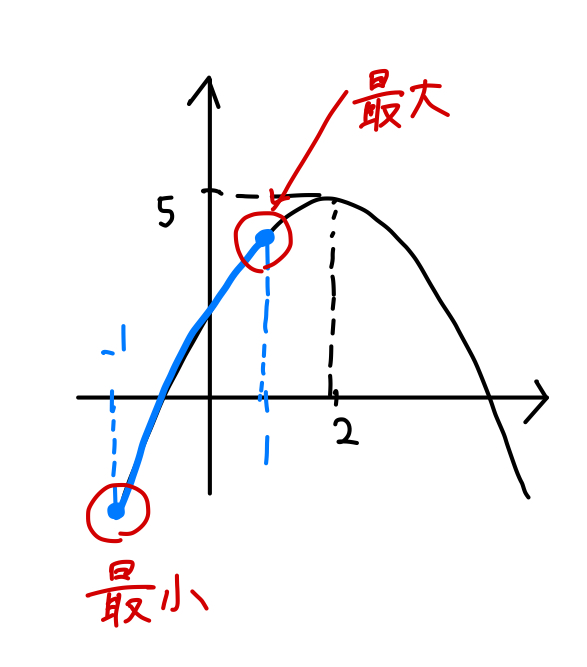
グラフより、$y=1$ のとき最大値$4$

$y=-1$ のとき最小値$-4$ となる。

$y=1$ を $x^2=1-y^2$ に代入すると $x=0$

$y=-1$ を $x^2=1-y^2$ に代入すると $x=0$

したがって

$x=0, y=1$ のとき最大値$4$

$x=0, y=-1$ のとき最小値$-4$

ポイント！

条件が二次式$x^2$, $y^2$ の場合、実数条件 $(実数)^2≧0$ を使って範囲を求めよう！

条件式なしの2変数関数の最大・最小

【問題】

$x,y$ が実数の値をとりながら変化するとき，$x^2-4xy+5y^2+2x-2y+7$ の最小値，およびそのときの $x,y$ の値を求めよ。

条件が指定されていないとき、$x,y$ のどちらか一方の文字に着目して平方完成していく。

今回の問題では、$x$に着目して平方完成していくと

$$\begin{eqnarray}&&x^2-4xy+5y^2+2x-2y+7\\[5pt]&=&x^2+(2-4y)x+5y^2-2y+7\\[5pt]&=&\{x+(1-2y)\}^2-(1-2y)^2+5y^2-2y+7\\[5pt]&=&(x-2y+1)^2-1+4y-4y^2+5y^2-2y+7\\[5pt]&=&(x-2y+1)^2+y^2+2y+6 \end{eqnarray}$$

ここまで変形することができたら、

次は、定数項$ y^2+2y+6 $ を平方完成していきましょう。

$$\begin{eqnarray}&&(x-2y+1)^2+y^2+2y+6\\[5pt]&=&(x-2y+1)^2+(y+1)^2+5 \end{eqnarray}$$

ここで $(x-2y+1)^2≧0$, $(y+1)^2≧0$ だから

$$(x-2y+1)^2+(y+1)^2+5 ≧5$$

等号が成り立つのは

$x-2y+1=0$ , $y+1=0$ のときなので

これを解くと $x=-3, y=-1$ となる。

したがって

$x=-3, y=-1$ のとき最小値$5$

ポイント！

条件が指定されていない場合、どちらかの文字に着目して平方完成する。

$X,Y$ が実数のとき、$X^2+Y^2$ は$X=Y=0$ のとき最小値となる。

【問題】

$x≧0$, $y≧0$ のとき，$x^2+5y^2+4xy-6x-4y-2$ の最小値を求めよ。

まずは、$x$に着目して平方完成していきましょう。

$$\begin{eqnarray}&&x^2+5y^2+4xy-6x-4y-2\\[5pt]&=&x^2+(4y-6)x+5y^2-4y-2\\[5pt]&=&\{x+(2y-3)\}^2-(2y-3)^2+5y^2-4y-2\\[5pt]&=&(x+2y-3)^2-4y^2+12y-9+5y^2-4y-2\\[5pt]&=&(x+2y-3)^2+y^2+8y-11\\[5pt]&=&(x+2y-3)^2+(y+4)^2-27 \end{eqnarray}$$

$(y+4)^2≧4^2=16$ , $(x+2y-3)^2≧0$ なので

$$(x+2y-3)^2+(y+4)^2-27≧16+0-27=-11$$

等号が成り立つのは

$x+2y-3=0$ , $y+4=4$ のときなので

これを解くと $x=3, y=0$ となる。

したがって

$x=3, y=0$ のとき最小値$-11$