今回は、連立方程式と比を融合させた問題について解説していきます。
$$\begin{eqnarray} \left\{ \begin{array}{l} 2x + 3y = 14 \\ x:y = 3:5 \end{array} \right. \end{eqnarray}$$
こんなやつだね…
なんか難しそう!!
と、思ってはいけません。
比例式の性質を知っておけば楽勝です(^^)
YouTubeでの動画解説はこちら!
[スタセミ中2バナー]
【連立方程式】比を含んだ文章題の解き方は??
まずは、比例式の性質を思い出しておきましょう。
~比例式の性質~
$$a:b=c:d$$
ならば
$$bc=ad$$
このように等式を作ることができます。
いわゆる「内内=外外」ってやつですね。
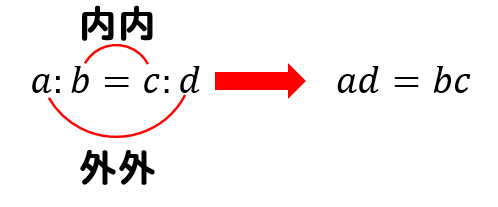
これを用いて連立方程式を解いていきましょう。
【連立方程式】比を含んだ方程式の解き方①
次の連立方程式を解きなさい。
$$\begin{eqnarray} \left\{ \begin{array}{l} 2x + 3y = 14 \\ x:y = 3:5 \end{array} \right. \end{eqnarray}$$
まずは、比例式になっている部分を「内内外外」を使って等式の形にしましょう。
$$x:y = 3:5$$
$$5x=3y$$
こうなれば、連立方程式も見慣れた形になりますね。
$$\begin{eqnarray} \left\{ \begin{array}{l} 2x + 3y = 14 \\ 5x = 3y \end{array} \right. \end{eqnarray}$$
ここからは今まで通りの解き方で解いていきましょう。
今回は、代入法を使って解いていきます。
\(5x=3y\) を\(2x + 3y = 14\) に代入すると
$$2x+5x=14$$
$$7x=14$$
$$x=2$$
\(x=2\) を\(2x+3y=14\) に代入すると
$$2\times 2+3y=14$$
$$4+3y=14$$
$$3y=10$$
$$y=\frac{10}{3}$$
となりました。
よって、連立方程式の解は
$$(x,y)=\left(2, \frac{10}{3} \right)$$
次は、ちょっと複雑なパターンもやってみましょう!
【連立方程式】比を含んだ方程式の解き方②
次の連立方程式を解きなさい。
$$\begin{eqnarray} \left\{ \begin{array}{l} (x+1) :(y-2) = 2:3 \\ x:y = 1:3 \end{array} \right. \end{eqnarray}$$
両方とも比例式になっている!
比例式にかっこがついている!
そんな状況でも解き方は一緒、まずは比例式を等式に変えちゃいましょう。
$$(x+1) :(y-2) = 2:3$$
$$3(x+1)=2(y-2)$$
$$3x+3=2y-4$$
$$3x-2y=-7$$
$$x:y = 1:3$$
$$3x=y$$
$$\begin{eqnarray} \left\{ \begin{array}{l} 3x-2y=-7 \\ 3x=y \end{array} \right. \end{eqnarray}$$
このように見慣れた連立方程式にしてやることができます。
あとは解くべし!
\(3x=y\) を\(3x-2y=-7\) に代入すると
$$y-2y=-7$$
$$-y=-7$$
$$y=7$$
\(y=7\) を\(3x=y\) に代入すると
$$3x=7$$
$$x=\frac{7}{3}$$
よって、連立方程式の答えは
$$(x,y)=\left(\frac{7}{3}, 7\right)$$
かっこがついて比例式について、もう少し復習したい方は
こちらもどうぞ(^^)

【連立方程式】比を含んだ方程式の文章題
最後は、文章問題に挑戦してみましょう!
ある中学校の男子の人数を \(x\)人、女子の人数を \(y\)人とすると
という部分から、次の比例式を作ることができます。
$$11:10=x:y$$
これを等式で表すと
$$10x=11y$$
となりますね。
次のこの部分から、部活をしている女子は80人と分かります。
更に、部活をしていない人の人数にも注目しましょう。
| 男子 | 女子 | |
| 全体の人数 | $$x$$ | $$y$$ |
| 部活している | $$120$$ | $$80$$ |
| 部活していない | $$x-120$$ | $$y-80$$ |
すると、上の表のようにまとめることができます。
よって
この部分から、次のような比例式を作ることができます。
$$(x-120):(y-80)=5:6$$
これを等式の形にすると
$$6(x-120)=5(y-80)$$
$$6x-720=5y-400$$
$$6x-5y=320$$
これで2つ式が作れたので、あとは連立方程式を解いていきましょう。
$$\begin{eqnarray} \left\{ \begin{array}{l} 10x=11y \\ 6x-5y=320 \end{array} \right. \end{eqnarray}$$
\(10x=11y\) を\(\displaystyle{x=\frac{11}{10}y}\) に変形し、\(6x-5y=320\) に代入すると
$$6\times \frac{11}{10}y-5y=320$$
$$\frac{33}{5}y-5y=320$$
$$33y-25y=1600$$
$$8y=1600$$
$$y=200$$
\(y=200\) を\(\displaystyle{x=\frac{11}{10}y}\)に代入すると
$$x=\frac{11}{10}\times 200=220$$
以上より
この中学校の男子は220人、女子は200人となります。
【連立方程式】比を含んだ計算まとめ!
お疲れ様でした!
比を含んだ連立方程式では、比例式の性質を覚えておくことが大事。
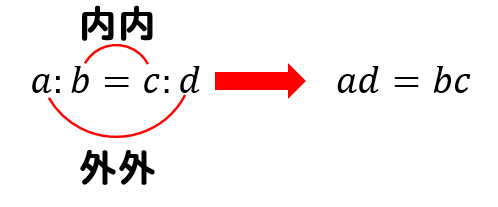
あとは、どうしても計算が複雑になりがちなので
代入法の解き方であったり、分数を含む連立方程式の計算に慣れておく必要がありますね。
こちらの記事で、連立方程式の基礎練習ができるようにしているので参考にしてみてください(^^)
>【連立方程式】加減法、代入法の簡単な練習問題!これでテストはバッチリ!!














コメントを残す