【作図】円に内接する正三角形の作図方法とは？

今回は、中１で学習する作図単元から

円に内接する正三角形の作図方法について解説していくよ！

問題
下の図で示した円周上に3頂点A、B、Cがあり、正三角形となる△ABCを考える。下に示した円周上に、正三角形となる△ABCを定規とコンパスを用いて作図しなさい。

この作図は、かなり上級者向けの問題になります。

公立高校の入試には出題はされないような難しい問題ですが

難関高校を受験する場合には、ぜひ解けるようにしておきたい1問です。

それでは、解説していきます。

正三角形を作図するための考え方

正三角形とは、すべての辺の長さが等しい三角形のことですね。

ということで、円の中に3辺がすべて等しくなるような三角形を作図したいです。

どのように同じ長さの辺をとるかというと

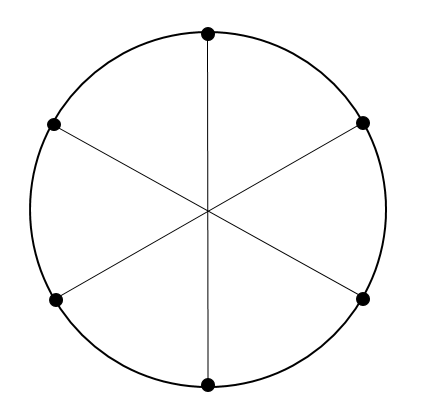
このように円を6等分してやります。

ちなみに6等分されている円の中心角は60°だね。

これもポイントだから覚えておいてね。

すると

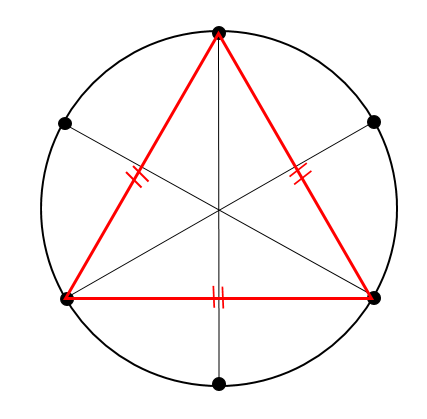
このように1個飛ばして点を結んでやると

同じ長さの辺を3つ作ることができます。

よって

この三角形は正三角形になる！

完成！！

ということです。

つまり

円を6等分することができれば

正三角形を作ることができるというわけですね。

作図手順の解説

それでは、まず円を6等分していきましょう！

そのためには、円の中心を求める必要があるので

円の中心を作図してやります。

円の中心は、円周上のどの点からも等しい距離にある点です。

ということで、弦の垂直二等分線をかくことで

円の中心を求めてやります。

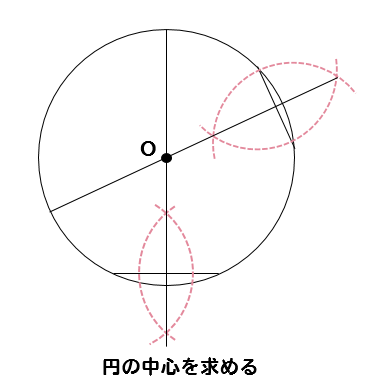
次に、先ほどかいた垂直二等分線と円の交点を点Aとして

点Aを中心とする半径AOの円をかいてやります。

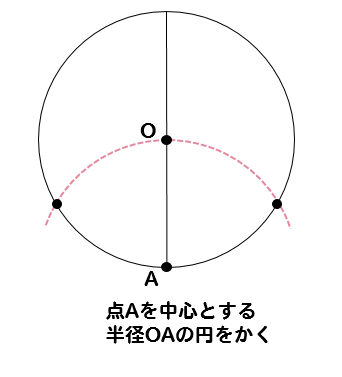
円と円が交わるところに点をとって

それぞれの点を線で結んでやると

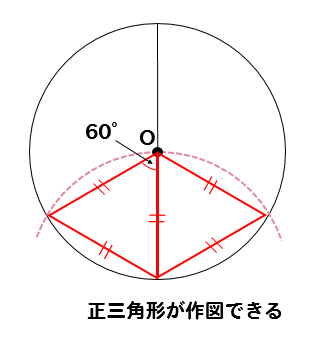
このように正三角形を作ってやることができます。

つまり、60°の角が作図できたことになります。

これらの線を延長してやると

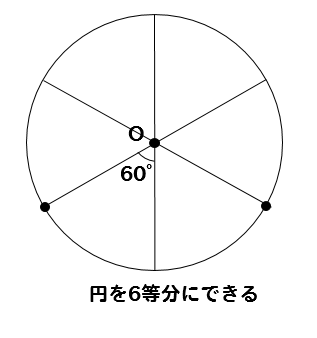
中心角が全部60°になってるよね

ということで…

6等分の完成です！！

6等分が完成すれば

1個飛ばして点を結んでやるだけです。

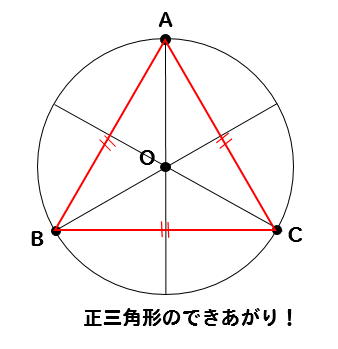
まとめ

お疲れ様でした！

なかなか複雑な作図でしたね(^^;

最後に手順をまとめておきましょう。

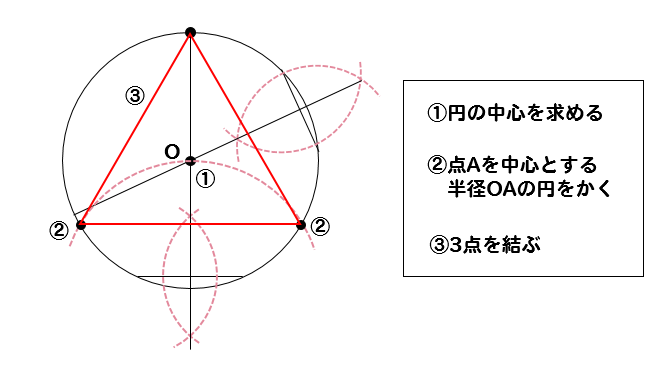
上では詳しく解説するために

わざと6等分の線をかきましたが

正三角形がかければOKなので

実際にはこのように3点を作図できたら

線で結んでやってください。

作図問題って

初めての挑戦では、すごく難しいですよね。

でも、１度解いたことある問題であれば

ほんっとに楽勝で解くことができます。

たくさん問題を解いて、知識を増やすこと

これが作図向上の近道だ！

こちらに入試の過去問を抜粋した記事もあるので

よかったら挑戦してみてください。

【高校入試】作図の過去問題を演習しよう！

ファイトだー(/・ω・)/