今回は、みんな大嫌いおうぎ形についての解説です!
なんで、おうぎ形って苦手な人が多いのでしょうかね?
やっぱり公式を覚えたりするのが難しく感じるのかな?
そんなおうぎ形の問題の中でも
ほんと正解率の低い『中心角を求める』という問題にスポットを当ててみたいと思う。
ちゃんとやり方を覚えれば難しくないからね
しっかりと学んでいってくださいな
ちなみに
おうぎ形の中心角を求める方法は大きく分けて3パターンあります。
- 方程式を利用し求めるパターン
- 比を使って求めるパターン
- ちょっと楽して公式パターン
ん?ちょっと楽できるバターンがあるの??
って思ったよね。
それがね
楽できるんだよ!
という訳で、順にそれぞれの解き方を解説していくので自分にあった方法を身につけてもらえればと思います。
今回の内容はこちらの動画でも解説しているので参考にしてみてね^^
方程式を利用して求めるパターン
問題
半径が3㎝で面積が3π㎠であるおうぎ形の中心角を求めなさい。
まずは、求めたい中心角をxと表します。
おうぎ形の面積が問題で与えられているので
面積の公式
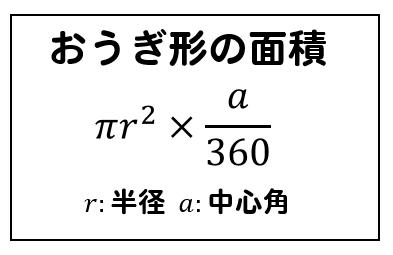
にそれぞれ分かっている数を当てはめていきます。
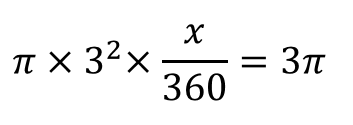
するとこんな式になりますね。
あとは、xを求める方程式を解いていけば良いです。
約分できるところは先に約分してやりましょう。
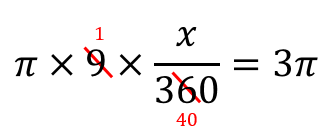
両辺についているπは消してやります。
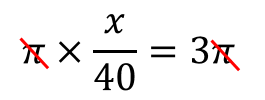
分数を消すために両辺に×40をしてやると
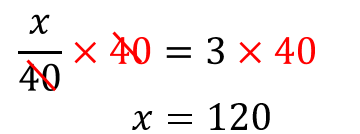
よって、中心角は120°となります。
弧の長さが与えられている場合も
考え方は同様です。
弧の長さを求める公式に数を当てはめて計算していけばOKです。
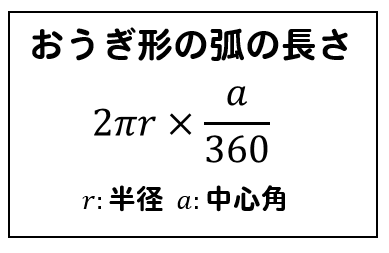
ポイントとしては
- 約分は先にやってしまう。
約分せずに計算してしまうと、あとで計算がややこしくなってきてミスに繋がっちゃうからね。なるべく式を作った段階でやってしまおう
- 両辺のπは消してしまう。
これも式を作った段階で消してしまうのがおススメです。なんでπが消えちゃうの?って疑問に思う方も多いと思いますが、2年生で文字の割り算を詳しく学習するので、そのときに謎は解けるはずですよ^^
まぁ、両辺をπで割ってやっただけなんですけどね。

比を使って解くパターン
次は比を使って解くパターンです。
おうぎ形と同じ半径を持つ円を比較しながら比を作っていきます。
上と同じ問題で考えてみると
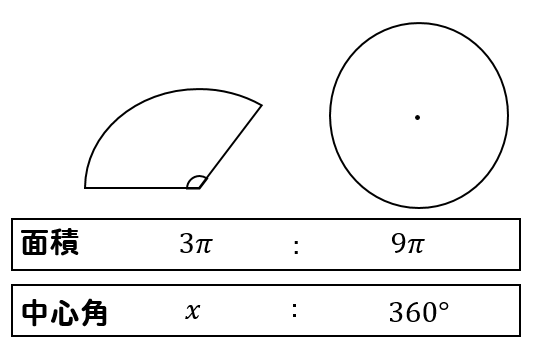
おうぎ形の面積は3πで中心角はxです。
それに対して、同じ半径(3㎝)を持つ円の面積と中心角を考えると9πと360°になります。
※円の中心角は常に360°です。
そして
それぞれの面積、中心角を比較して比を取っていきます。
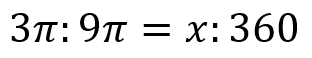
比例式が完成すれば『内内外外の性質』を使って計算。
ただし、比が簡単に出来る場合には簡単にしてしまいましょう。
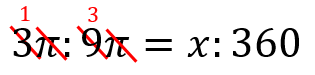
πも先に消しちゃいます。
比が簡単に出来たら方程式にして計算していきます。
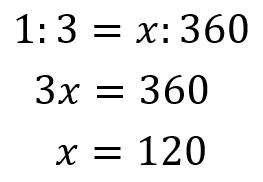
すると中心角は120°と求めることができました。
弧の長さが与えられている問題では、弧の長さと円周の長さで比を取るようにしてください。
比例式の計算を忘れてしまった方はこちらで確認しておいてくださいね!
どうでしたか?
方程式を使って解くパターンよりは計算が少なかったですかね。
このパターンのポイントとしては
- おうぎ形の弧と円の円周の長さを比較
- おうぎ形の面積と円の面積を比較
- それぞれの中心角を比較
おうぎ形と円の比較が大事なポイントでした。
でもさ、それでもやっぱり…
比の計算ってちょっと面倒じゃないですか…?
というわけで
中心角を求めるときには
比の途中の計算を省いたこの形を覚えておくと
かなーーーり楽になるんだよね
というわけで、次はちょっと楽して公式パターン
ちょっと楽して公式パターン
次の公式を覚えておけば、あとは数を当てはめていくだけで中心角が求めれちゃうという、その名も『ちょっと楽して公式パターン』です。




まぁ、これは比を使った考え方を少し応用した公式なので、発想は一緒です。
おうぎ形と円を比べてるわけです。
それでは、どのように使うか実践してみます。
今までと同じ問題
半径3cmで面積が3π㎠のおうぎ形の中心角を求めます。
まずは同じ半径(3㎝)を持つ円の面積を求めます。
3×3×π=9π
あとは公式に当てはめていくと


式が完成します。
あとは約分してやって、計算あるのみ!
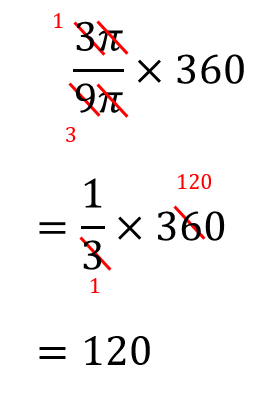
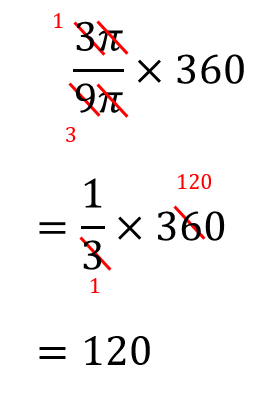
これで中心角が120°だと求めることができました。
どうですか?
今までのパターンに比べたら格段に簡単になったと思いませんか?
そう思えた方は今後、このパターンを使いこなしていってください。
解くスピードも正確性も向上するはずです!
それでは、最後は演習問題で確認していきましょう。
練習問題で理解を深める!
次のおうぎ形の中心角を求めなさい。
(1)半径12㎝、弧の長さ3π㎝のおうぎ形
(2)半径9㎝、面積9π㎠のおうぎ形
それでは(1)から確認していきましょう。
(1)半径12㎝、弧の長さ3π㎝のおうぎ形
次は(2)の解説をどうぞ!
(2)半径9㎝、面積9π㎠のおうぎ形
おうぎ形の中心角の求め方 まとめ
おうぎ形の中心角を求める方法は大きく分けて3つのパターンがありました。
- 方程式を利用して求めるパターン
- 比を使って求めるパターン
- ちょっと楽して公式パターン
今回は『ちょっと楽して公式パターン』を推し気味で解説しちゃったんだけど、もちろんそこは好みだから!
自分がしっくりくる解き方でやってもらえればOKです。
中心角を求める問題は、ちょっと応用に分類される問題だから
解けるようになっておけば、他の人とも差がつけれるね!
だから、ぜーーったいに身につけておこう!
ファイトだ!
おうぎ形の中心角を求める3つのパターン! ←今回の記事




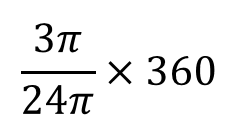
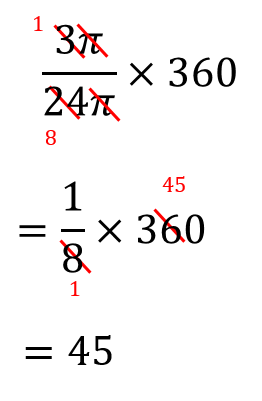
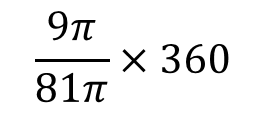
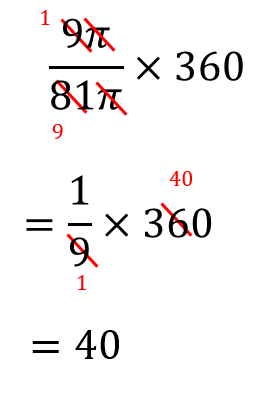














分かりやすい!
役に立つ事ばっかりで次のテストも頑張れそうです!
ありがとうございます(^^)
テスト頑張ってください!
公式があると、安心するので分かってよかったです!
お役に立てて良かったです!
中心角が求めれるようになると
一気に応用力が高まりますね!
ちょー分かりやすかったです!
他のページ見たんですけどなんか言っていることわかんなくって、、、
でも、このサイトみて一瞬で分かりました!定期テストでいい点取れる気満々になりました!!
同感です♪
よかったです^^
テストがんばってくださいね!!
詳しく書かれていてとてもわかりやすかったです!(๑˃̵ᴗ˂̵)
ありがとうございます!
ぜひ、おうぎ形マスターを目指してください^^
わかりやすかったです
難しかったけど理解できました!!!