今回は、過去に入試に出題された問題である
円錐を転がすと1周するのにどれくらい回転する?
といった問題を解説していきます。
問題
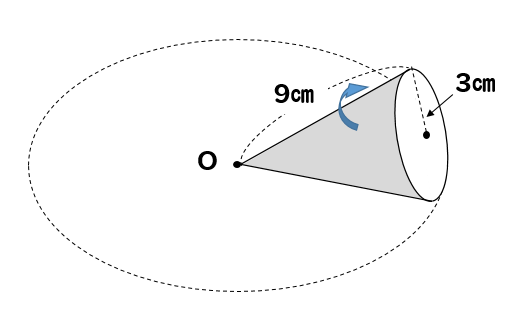
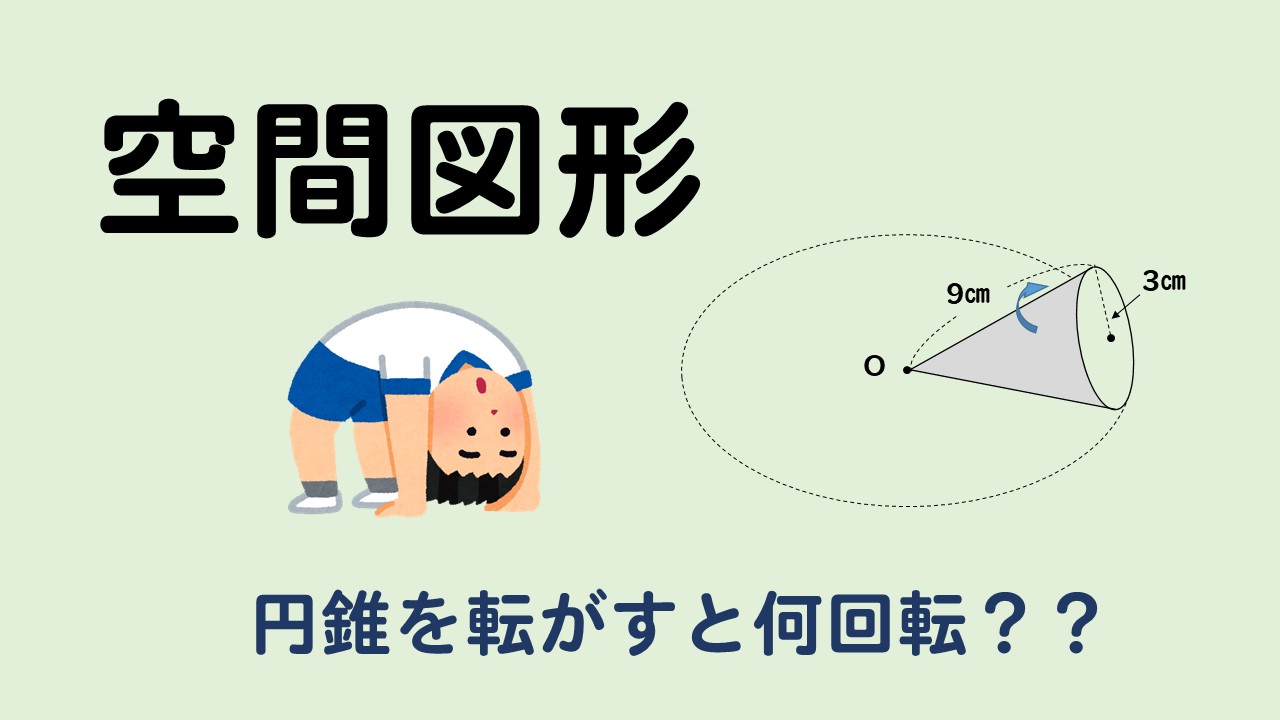
下の図のように、底面の半径が3㎝で、母線の長さが9㎝の円錐を平面上におき、頂点Oを中心としてすべらないように転がす。このとき、点線で示した円の上を1周してもとの場所にかえるまでに何回転するか求めなさい。
こちらの動画も合わせてご活用ください^^
問題の答え&解説
円錐を転がす問題のポイントは
転がすコースである点線部分の長さと
円錐の底面の周の長さを比べることです。
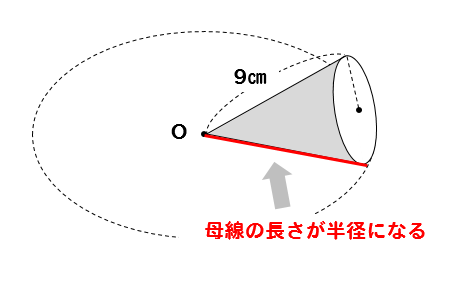
点線部分の円は、円錐の母線が半径になっているよね。
だから、半径は9㎝となり
円周の長さは\(2\pi\times 9=18\pi\)(cm)となります。
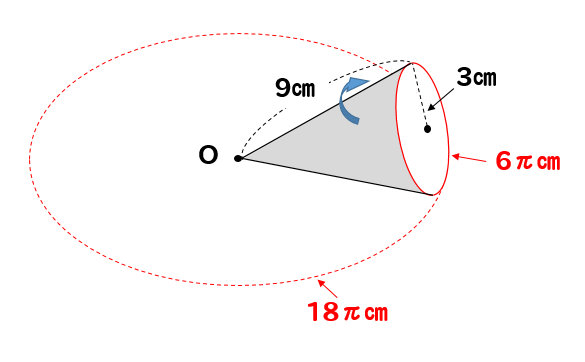
円錐の底面は、半径が3㎝なので
円周の長さは\(2\pi\times 3=6\pi\)(cm)となります。
円の公式が必要だからちゃんと思い出しておいてね!
$$2\pi\times (半径)$$
それぞれの値が求まったら
回転させたときの状況を考えてみましょう。
円錐を1回転させると、底面部分の\(6\pi\)(cm)だけ
点線部分のコースを進むことになります。
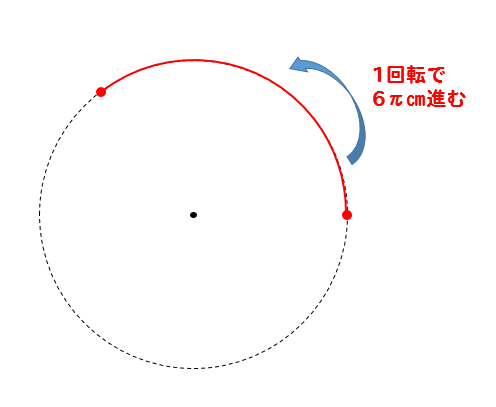
点線部分のコースは\(18\pi\)(cm)、1回転で\(6\pi\)(cm)進む。
ということは、1周するのにどれくらい回転するかは割り算をすればよいですね。
$$18\pi \div 6\pi=3$$
よって、1周するのに3回転するということがわかります。
答え
3回転
以上!
見るべきポイントが分かっていれば簡単な問題でしたね(^^)
回転数を求める手順
- 母線を半径とするコース部分の円周の長さを求める
- 回転させる円周の底面である円の円周の長さを求める
- (1で求めた値) ÷ (2で求めた値)を計算する
それでは、同様の問題で
発展問題にも挑戦してみましょう。

円錐を回転させる問題から表面積へ!
問題
下の図のように、底面の半径が4㎝の円錐を平面上におき、頂点Oを中心としてすべらないように転がす。このとき、円錐は4回転したところでもとの位置に戻ってきた。このとき、転がした円錐の表面積を求めなさい。

この問題では、母線の長さが与えられていない代わりに
4回転でちょうど1周するということがわかっています。
この情報から、円錐の母線を求めて
表面積を考えていきましょう。
円錐の底面の円周の長さが\(2\pi\times 4=8\pi(cm)\)であることから
この円錐は1回転するごとに\(8\pi(cm)\)進むことがわかります。
これが4回転すると、ちょうど1周するので
コースの全長は
$$8\pi \times 4=32\pi(cm)$$
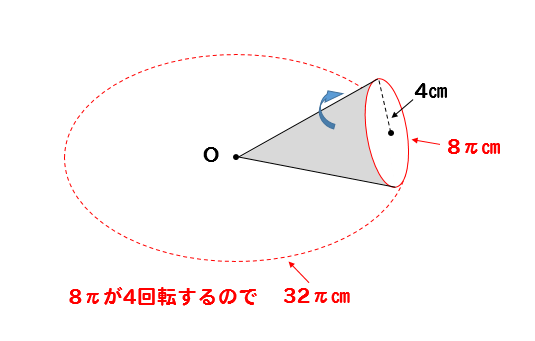
ということがわかります。
すると
点線部分の円の半径を\(x\)とすると
$$2\pi x=32\pi$$
$$x=16$$
となるので、半径は16㎝ということがわかります。
この円の半径と、円錐の母線の長さは同じになるので
求めたい円錐の情報をまとめるとこんな感じになります。
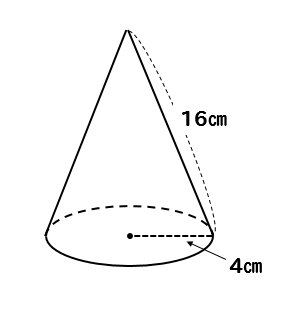
母線がわかれば、円錐の表面積を求めることができるようになりますね!
円錐の表面積は裏ワザ公式を使えば一発です!

今回は、中心角は必要ないので
側面積だけ、裏ワザ公式を使って求めます。

側面積は、母線と半径と\(\pi\)を掛けて\(64\pi\)
底面積は、半径×半径×\(\pi\)で\(16\pi\)
表面積はそれぞれの値を合わせて
$$64\pi + 16\pi=80\pi (cm^2)$$
となります。
答え
$$80\pi (cm^2)$$
まとめ
お疲れ様でした!
円錐を転がす問題では
転がすコースの全長と円錐の底面の長さを比べることがポイントです。
それぞれの値が分かれば、どれだけ回転させればよいかがわかります。
また、底面の円周の長さと回転数がわかれば
そこからコースの全長を求めることもできますね。
というわけで
(コースの全長)÷(底面の円周の長さ)=(回転数)
(底面の円周の長さ)×(回転数)=(コースの全長)
この2つの関係をおさえておければバッチリでしょう!
ファイトだー(/・ω・)/
















コメントを残す