【二次方程式の利用】箱の容積を考える文章問題を解説！

今回は二次方程式の利用から

箱の容積を考える文章問題について解説していくよ！

 

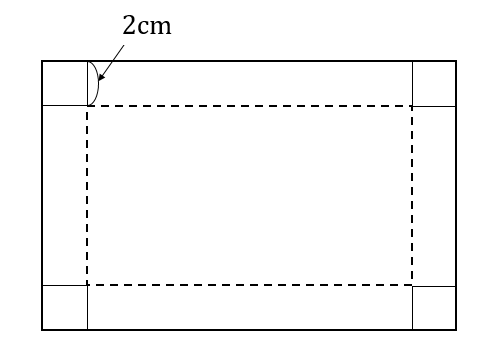
箱の容積を考える問題とは、こんなやつだね。

 

動画でサクッと理解したい方はこちらをどうぞ(‘◇’)ゞ

 

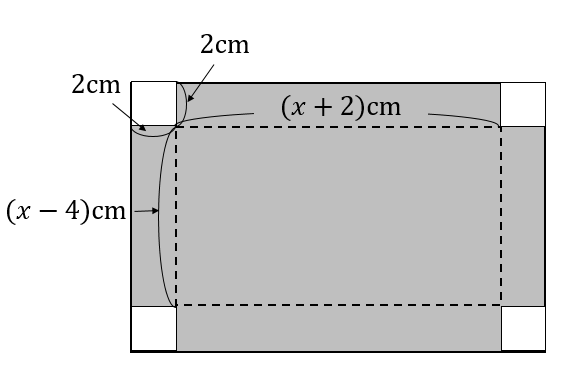
対応する辺をおさえておこう！

今回の問題では、展開図を組み立てて箱を作るわけですが

展開図と箱のどの部分が対応するのかをおさえておきましょう。

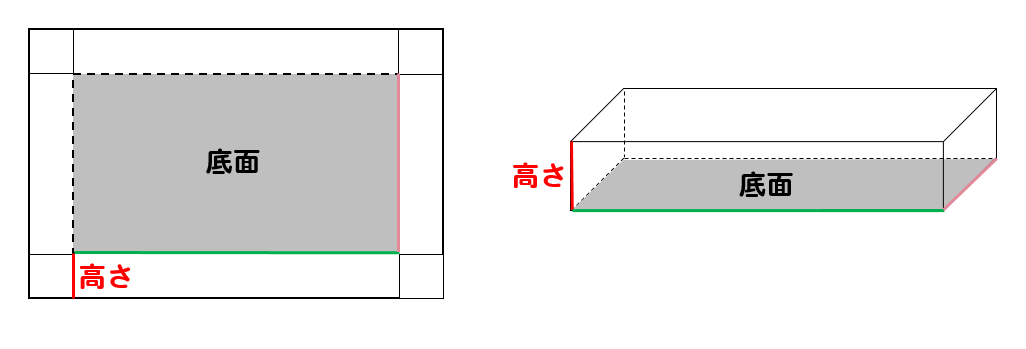
色を付けた部分が対応する辺です。

どこの部分が箱の辺になるのかイメージを持っておくことが大切です。

 

特に重要なのは、底面と高さに関する辺です。

 

容積の求め方は？

今回の問題では、容積の求め方も知っておく必要があります。

容積とは、この容器に入れることができる量を表す値ですが

体積と同様の求め方で表すことができます。

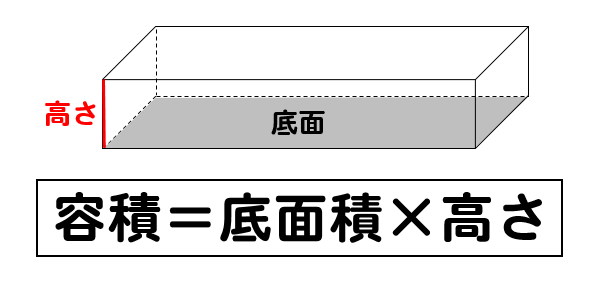
この求め方も覚えておきましょう！

 

問題の解説＆答え

それでは、今回の問題を考えていきましょう。

まずは、求めたい縦と横の長さを文字で表していきます。

厚紙の縦の長さを\(x\)cmとすると

横の長さは、縦の長さより5㎝長いので\((x+5)\)cmと表すことができます。

 

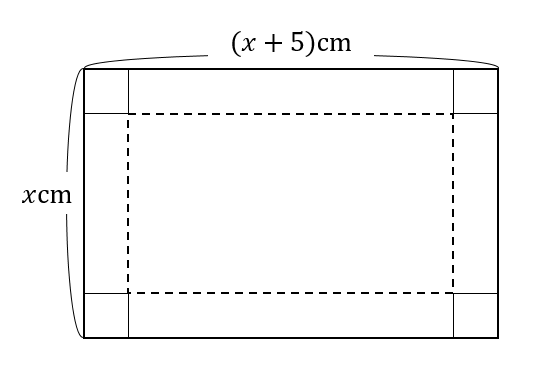
これを基準に底面積や高さを求めていきます。

 

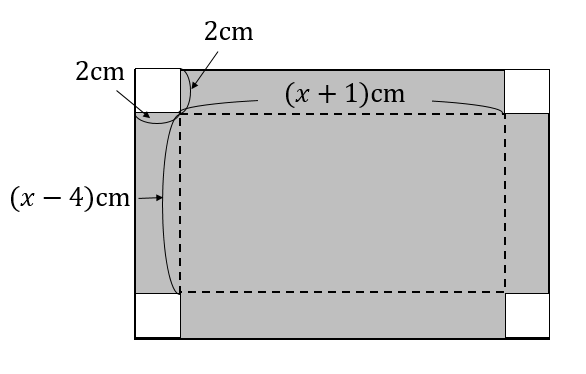
底面の縦の長さは

\(x\)cmから四隅の2㎝を2つ分引いて

\(x-2-2=(x-4)\)cmと表せます。

 

底面の横の長さは

\((x+5)\)cmから四隅の2㎝を2つ分引いて

\((x+5)-2-2=(x+1)\)cmと表せます。

 

高さは、切り取る四隅の1辺の長さを見ればよいので

\(2\)cmと表せます。

 

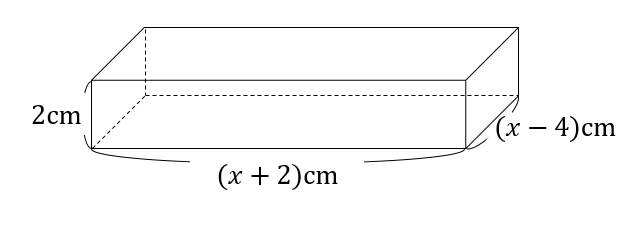
組み立てるとこんな感じですね。

 

 

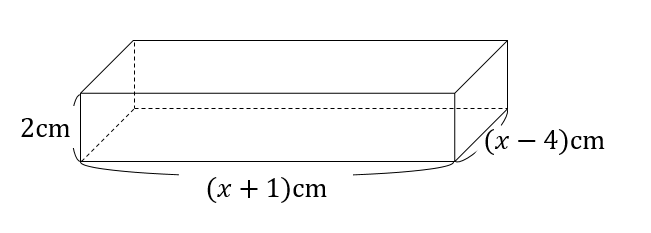
それぞれの辺の長さが揃ったところで容積を求めていきましょう。

底面積は

$$(x+1)\times (x-4)$$

なので

容積は

$$(x+1)(x-4)\times 2$$

と表せます。

 

 

そして、この容積が100㎝³になることから方程式を作ってやります。

$$2(x+1)(x-4)=100$$

両辺を2で割ると

$$(x+1)(x-4)=50$$

$$x^2-3x-4=50$$

$$x^2-3x-54=0$$

$$(x-9)(x+6)=0$$

$$x=9,-6$$

辺の長さは負にはならないので\(-6\)は問題に適しません。

よって\(x=9\)となります。

 

これにより、縦の長さが9㎝ということがわかりました。

横の長さは縦より5㎝長いということなので14㎝となります。

 

よって、答えは

縦の長さ　9㎝、　横の長さ　14㎝

 

練習問題に挑戦！

 

 

 

【追加演習】二次方程式の文章題をパターン別に攻略せよ！

今回は二次方程式の文章題特訓として、パターン別の演習課題を用意しました。

ここでは定期テストによく出題される「ある数、自然について」「図形」「箱の容積」「道幅」「動点」といった問題を取り上げています。これらが完璧に解けるようになれば、自信をもってテストに挑めるようになりますよ(‘ω’)ノ

動画解説も用意しているので、苦手な文章題も挫折することなく最後まで取り組めるはず！がんばってください＾＾

 

追加演習をやってテストの点数をUPさせたい方には、課題プリントをメールで送らせてもらっています。

 

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

 

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

二次方程式の利用　箱の容積　まとめ

お疲れ様でした！

二次方程式の箱の容積を考える文章問題は

定期テストでは必須の問題です。

 

必ず解けるようにしておきましょう。

ポイントは

このように、それぞれの辺を\(x\)を用いて表せるかどうかですね。

 

 

文字で表すことができれば

あとは方程式を計算していくだけなので楽勝です！

ただし、練習問題で解いたように

答えがキレイな値にならず

ルートが含まれていたりすることもあるので

ちょっと注意ですね。

 

さぁ、練習あるのみだ！

ファイトだー(/・ω・)/