今回は中1で学習する作図の単元から
直角を三等分する線の作図方法について解説していきます。
直角を三等分するというのは、30°の角を3つ作るということです。
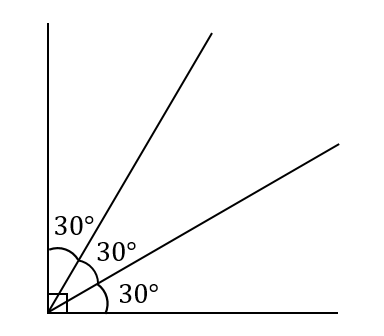
イメージ図としては、こんな感じですね!
それでは、直角の三等分線の作図方法について順を追って説明していきます!
Contents
正三角形で60°作る
まず、正三角形を作ることで60°の角を作りましょう。
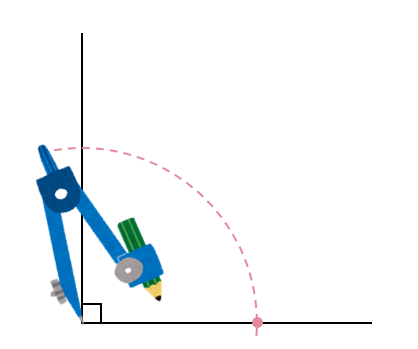
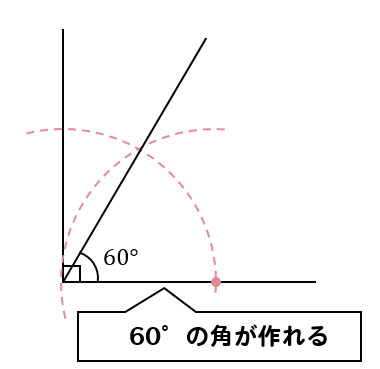
直角の部分に針を置いて、適当な長さの円をかきます。
半径の大きさは自由で良いですが小さすぎると次の過程が難しくなっちゃうので、程良い大きさにしましょうね。
円と直線との交点に針を置いて
先ほどの円と同じ長さの半径に持つ円をかきます。
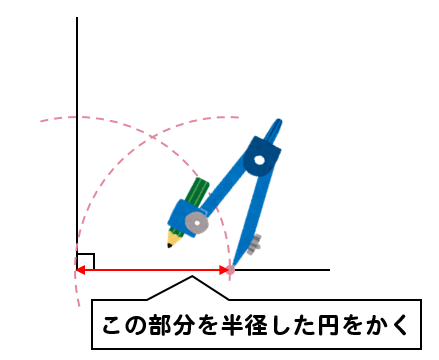
すると、正三角形が作れますね!
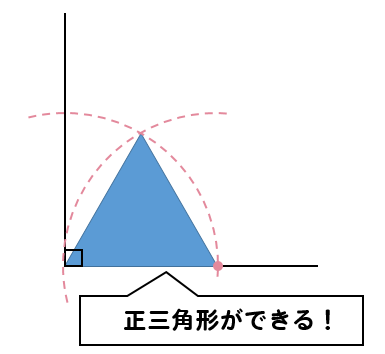
つまり、60°が作れたことになります。
もう一方から60度を作る
さっきと同様に、もう一方の交点から60°の角を作りましょう。
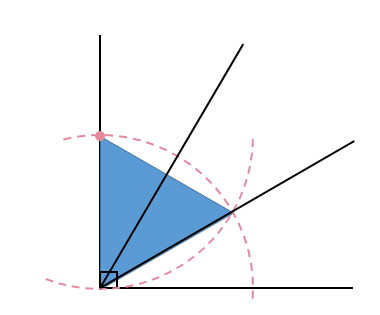
縦の線を共有するような正三角形を作図します。
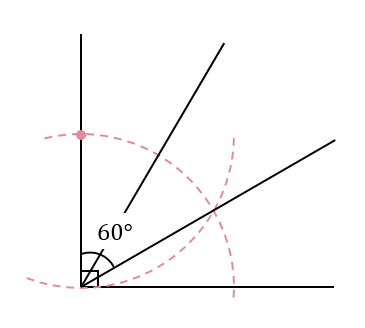
すると、このように60°の角を作ることができますね。

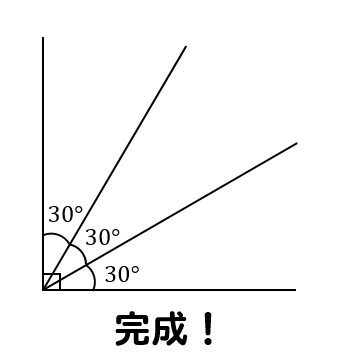
完成!
これで完成です!
え、なんで60°の角が作れたら完成なのかって??
直角(90°)の中に60°の角が作れたら

残り部分は30°になることがわかるよね。
よって、60°の角を2つ作ることで
30°の角が3つ作れたことになります。
直角の三等分線の完成です!
まとめ
お疲れ様でした!
それでは、最後に手順をまとめておきましょう。
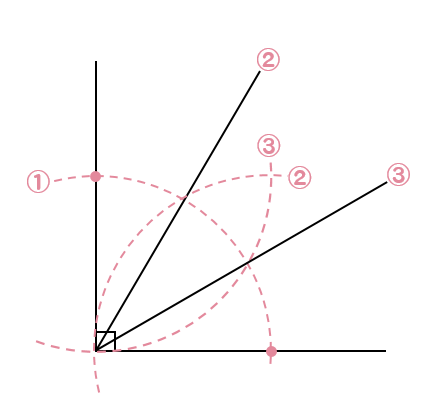
直角三等分線の手順
- 直角部分に針を置いて、適当な大きさの円をかく
- 直線と円との交点から、先ほどと同じ半径の円をかく
- 同様に、もう一方からも同じ半径の円をかく
以上!
もっと作図練習をしたい方は、こちらもどうぞ^^
















すごく分かりやすかったです!
おかげで、方程式のテストで、点数が上がりました✨
点数アップおめでとうございます!
嬉しい報告ありがとうございました^^