【苦手な人向け】条件付き確率の考え方を図を使ってイチからわかりやすく！

条件付き確率って、なんだか分かりにくい！

そもそも、どういう意味なんだろうか…

普通の確率と何が違うの…(+_+)

と、条件付き確率を苦手にしている方が多いです。

そこで、今回の記事では、そんな条件付き確率についてイメージがつかみやすいように図を使いながらイチから解説していきます。

今回の内容はこちらの動画でも解説しています！

動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします＾＾

高校メルマガ講座の無料登録はこちら！

Contents

条件付き確率とは、考え方と公式を紹介！
条件付き確率の例題を解いてみよう！
まとめ！

条件付き確率とは、考え方と公式を紹介！

事象Aが起こったことがわかっているとき、事象Bが起こる確率のことを、Aが起こったときのBが起こる条件付き確率といって、$P_{A}(B)$ と表します。

これまでの確率では、分母にくる数字は全部の場合の数でしたね。

ですが、条件付き確率の場合には、

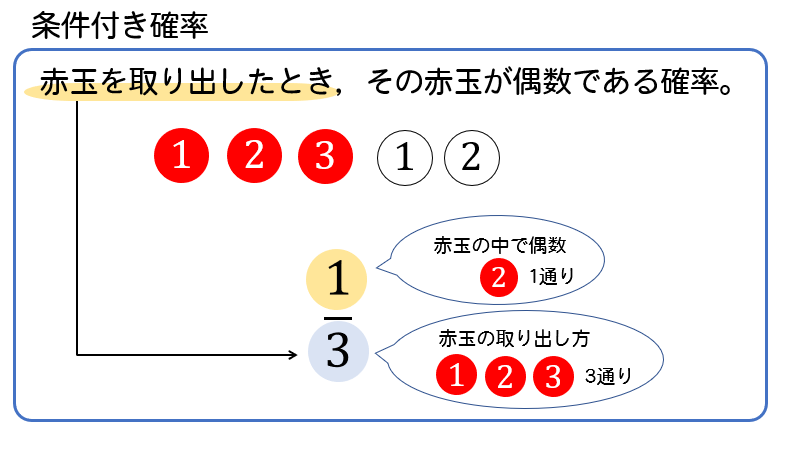
このように条件を満たす場合の数が分母にくるようになります。

「条件付き」の意味を考えてみれば分かるはずです。

では、想像してみましょう。

「赤玉を取り出したとき」というのは次のような状況をいいます。

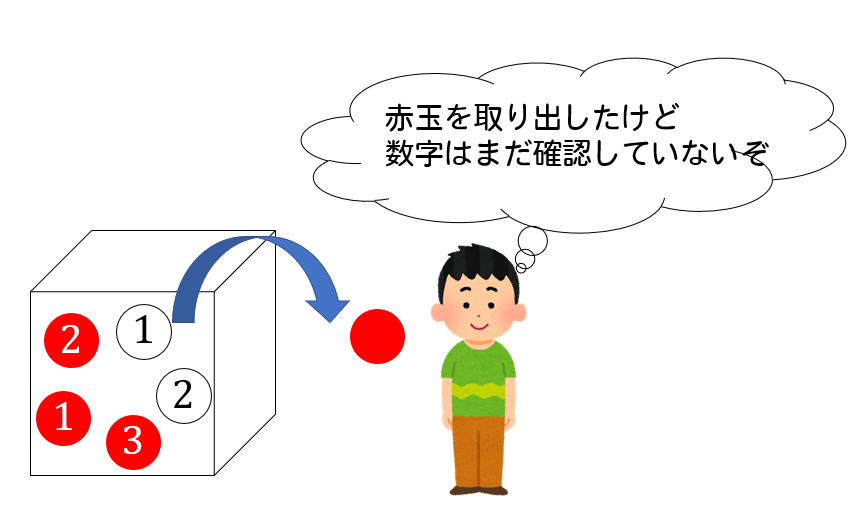
すでに赤玉を手に持っています。

しかし、数字はまだ確認していない。

こんな状況を表しています。

では、ここから玉に書かれている数字を確認していきます。

赤玉を手に持っている人からすると、

すでに可能性は赤1、赤2、赤3のいずれか3通りに限られています。

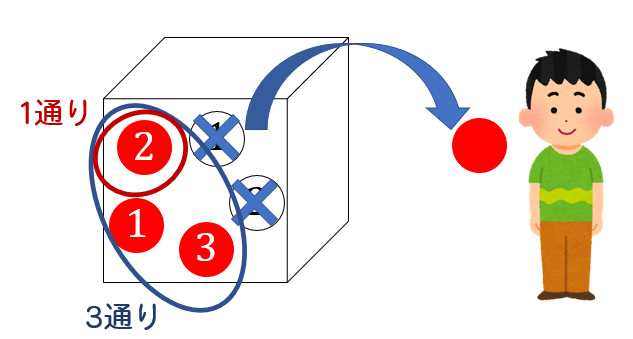
つまり、全部が3通り、その中で偶数なのは1通り。

その確率は $\frac{1}{3}$ である！

これが「条件付き確率」というものです。

これで条件付き確率のイメージが湧いたかな？？

これまでの確率は、全部の中でそれが起こる確率でした。

一方で、条件付き確率は、すでにあることが起こった状況の中で、それが起こる確率を考えるというものです。

では、以上のことを公式としてまとめると次のようになります。

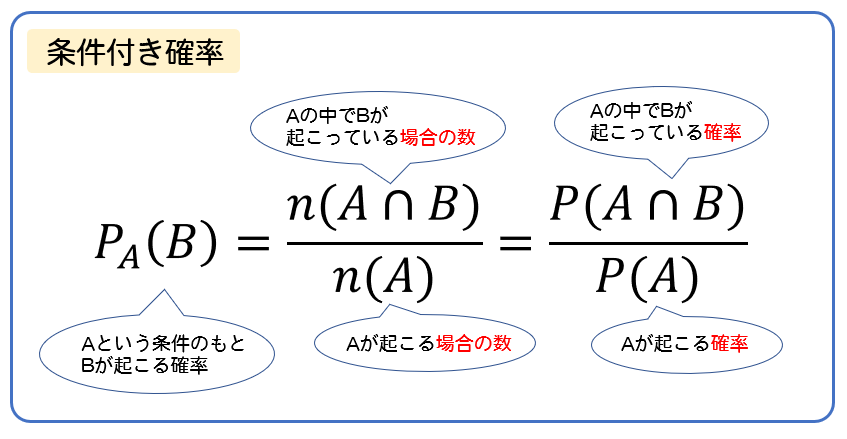
数式で覚えようとすると、ちょっと難しく思えちゃいますが(^^;)

イメージとしてはこんな感じで覚えておきましょう。

$$条件付き確率=\frac{条件の中でそれが起こっている}{条件が起こる}$$

また、上の具体例では場合の数を用いて条件付き確率を求めましたが、それぞれの確率を使っても求めることができます。

これは問題で与えられている情報によって使い分けるようにしてください。次章にて例題で紹介しますね。

また、もう1つ紹介しておきたい公式があります。

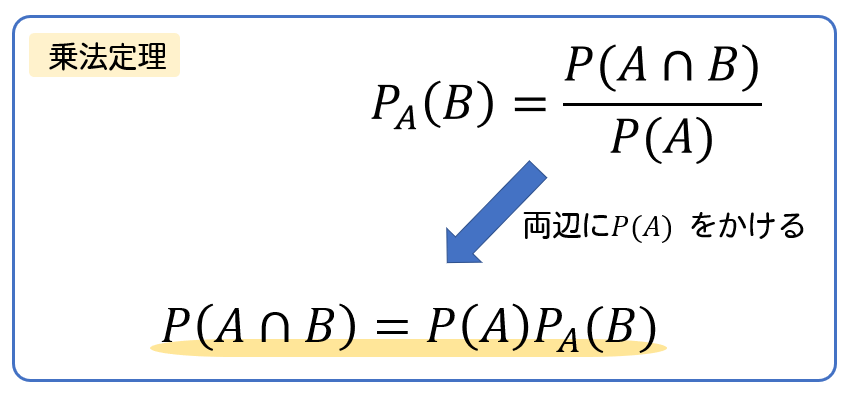
ちゃんと意味が分かっていれば、これは公式として覚えておくほどじゃないかな…

と思いますが、次の例題で具体的な使い方を確認しておきましょう。

【例題】

赤玉3個と白玉4個の入った袋から，玉を1個ずつ2個取り出す。ただし，取り出した玉はもとにもどさない。このとき，取り出した玉がすべて赤玉である確率を求めよ。

これまでの確率では、取り出した玉をもとに戻していましたね。

そのため、次に玉を取り出すときにはリセットされ、毎回同じ状態で確率を考えていきました。

しかし、今回のように「玉はもとにもどさない」場合

2回目以降に玉を取り出すときには、直前にどんな玉が取り出されたかによって確率が変わってきます。

そこで用いることになるのが、上で紹介した乗法定理です。

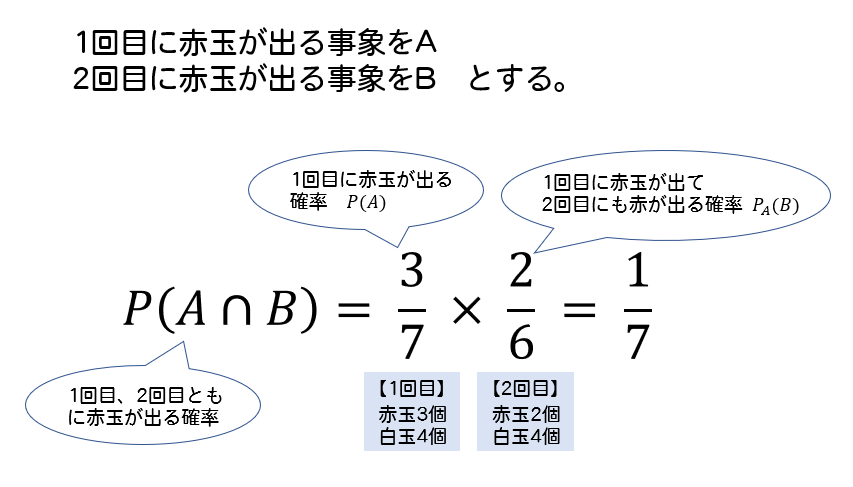
1回目に赤玉を取り出す確率は、赤玉3個白玉4個の状態だから $\frac{3}{7}$

1回目の赤玉が出た状態で、2回目に玉を取り出すときには赤玉2個白玉4個になっています。

よって、2回目も赤玉を取り出す確率は $\frac{2}{6}=\frac{1}{3}$

よって、求めたい確率は $\frac{3}{7}\times \frac{1}{3}=\frac{1}{7}$ となります。

例題で示した通り、これは公式でカチッと覚えるというよりも、そのときの状況を考えて毎回の確率を考えていくってことを徹底すれば問題ないかと思います(^^)

では、次章で条件付き確率の様々なパターンについて例題で解説していきます。

どんどん理解を深めていきましょう(/・ω・)/

条件付き確率の例題を解いてみよう！

【例題】

大小2個のさいころを同時に投げて，2つの目の和が6となる事象をA，2つの目の積が6以下となる事象をBとするとき，次の確率を求めよ。

（1）$P_{A}(B)$

（2）$P_{B}(A)$

（1）では、Aの事象を全部だと考え、その中にBの事象がどれくらい入っているかを考えれば良いです。

つまり、$P_{A}(B)$を求めるためには、$n(A)$, $n(A\cap B)$を求める必要があります。

2つの目の和が6となるのは、$(1,5)$, $(2,4)$, $(3,3)$, $(4,2)$, $(5,1)$ なので、$n(A)=5$

次に、Aの中で目の積が6以下となっているのは、$(1,5)$, $(5,1)$ なので、$n(A\cap B)=2$

以上より、

$$P_{A}(B)=\frac{n(A\cap B)}{n(A)}=\frac{2}{5}$$

答え

$$（1）P_{A}(B)=\frac{2}{5}$$

（2）では、Bの事象を全部だと考え、その中にAの事象がどれくらい入っているかを考えれば良いです。

つまり、$P_{B}(A)$を求めるためには、$n(B)$, $n(A\cap B)$を求める必要があります。

$n(A\cap B)$ は（1）で求めているので、あとは $n(B)$ を求めればよいですね。

2つの目の積が6以下となるのは、$(1,1)$, $(1,2)$, $(1,3)$, $(1,4)$, $(1,5)$, $(1,6)$, $(2,1)$, $(2,2)$, $(2,3)$, $(3,1)$, $(3,2)$, $(4,1)$, $(5,1)$, $(6,1)$ なので、$n(B)=14$

以上より、

$$P_{B}(A)=\frac{n(A\cap B)}{n(B)}=\frac{2}{14}=\frac{1}{7}$$

答え

$$（2）P_{B}(A)=\frac{1}{7}$$

【例題】

10本のくじの中に当たりくじが3本ある。一度引いたくじはもとに戻さない。初めにAくんが1本引き，次にBさんが1本引くとき，次の確率を求めなさい。

（1）Aくん，Bさんともに当たる確率

（2）Bさんが当たる確率

Aくんが当たりを引く事象をA，Bさんが当たりを引く事象をBとして話を進めていきます。

まずは（1）を考えてみましょう。

最初にAくんが当たる確率は、10本中当たりが3本の状態なので、$\frac{3}{10}$ となります。

Aくんが当たりを引いた後に、Bさんが当たりくじを引く確率。

このときは9本中当たりが2本の状態になっているので、$\frac{2}{9}$ となります。

以上より、

$$\begin{eqnarray}P(A\cap B)&=&P(A)P_{A}(B)\\[5pt]&=&\frac{3}{10}\times \frac{2}{9}=\frac{1}{15} \end{eqnarray}$$

答え

$$（1）P(A\cap B)=\frac{1}{15}$$

次に（2）Bさんが当たる確率ですが、これには2パターンの可能性があります。

Aくんが当たり　⇒　Bさんも当たり …①
Aくんがはずれ　⇒　Bさんは当たり…②

①のパターンは（1）で求めているので、②のパターンの確率を求めて①②の和を考えていきましょう。

では、②パターンのAくんがはずれて、Bさんは当たる確率は、

$\frac{7}{10}\times \frac{3}{9}=\frac{7}{30}$ となるので、

以上より、

$$\begin{eqnarray}P(B)&=&P(A)\times P_{A}(B)+P(\overline{A})\times P_{\overline{A}}(B)\\[5pt]&=&\frac{1}{15}+\frac{7}{30}\\[5pt]&=&\frac{3}{10} \end{eqnarray}$$

このことから、一番最初にくじを引くAくんが当たる確率は $\frac{3}{10}$

後からくじを引くBさんが当たる確率も $\frac{3}{10}$ となり、2つの確率が等しいことが分かります。

よって、くじびきで当たる確率というのは、くじを引く順番に関係ないってことですね！

答え

$$（2）P(B)=\frac{3}{10}$$

【例題】

ある製品を製造する2つの工場 $a, b$ がある。$a$ 工場の製品 $4\%$，$b$ 工場の製品には $3\%$ の不良品が含まれているとする。$a$ 工場と $b$ 工場で製造する製品の割合は $5:4$ である。$2$ つの工場で製造された多くの製品の中から，無作為に $1$ 個の製品を取り出すとき，次の確率を求めよ。

（1）不良品であった確率

（2）不良品であったとき，それが $a$ 工場の製品である確率

取り出した1個の製品が$a$ 工場の製品である事象をA，$b$ 工場の製品である事象をB、不良品である事象をCとする。

すると、$a$ 工場と $b$ 工場で製造する製品の割合は $5:4$ だから

$P(A)=\frac{5}{9}$, $P(B)=\frac{4}{9}$

$a$ 工場の製品 $4\%$，$b$ 工場の製品には $3\%$ の不良品が含まれているから

$P_{A}(C)=\frac{4}{100}=\frac{1}{25}$, $P_{B}(C)=\frac{3}{100}$

ここまで準備が整ったら各問題を考えていきましょう。

まず、（1）不良品であった確率。

不良品である確率は次の2パターンが考えられます。

$a$工場の不良品であるパターン　$P(A\cap C)$
$b$工場の不良品であるパターン　$P(B\cap C)$

よって、

$P(A\cap C)=P(A)P_{A}(C)=\frac{5}{9}\times \frac{1}{25}=\frac{1}{45}$

$P(B\cap C)=P(B)P_{B}(C)=\frac{4}{9}\times \frac{3}{100}=\frac{1}{75}$

以上より

$$P(C)=\frac{1}{45}+\frac{1}{75}=\frac{8}{225}$$

答え

$$（1）P(C)=\frac{8}{225}$$

（2）不良品であったとき，それが $a$ 工場の製品である確率とは、$P_{C}(A)$ですね。

よって、

$$\begin{eqnarray}P_{C}(A)&=&\frac{P(A\cap C)}{P(C)}\\[5pt]&=&\frac{\frac{1}{45}}{\frac{8}{225}}\\[5pt]&=&\frac{1}{45}\times \frac{225}{8}\\[5pt]&=&\frac{5}{8} \end{eqnarray}$$

答え

$$（2）P_{C}(A)=\frac{5}{8}$$