高校数学Aで学習する場合の数の単元から
「重複を許す組み合わせ」
について解説していきます。
重複を許す組み合わせとは次のような問題のことですね。
【問題】
りんご,みかん,バナナの3種類から重複を許して,4個取り出す組み合わせは全部で何通りあるか。
まずは、こちらの問題をどのような考え方で解けばよいのか解説します。
記事後半では、重複組み合わせのいろんなパターンについて例題を用いて解説していきます。
今回の内容はこちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
仕切りを使った考え方
【問題】
りんご,みかん,バナナの3種類から重複を許して,4個取り出す組み合わせは全部で何通りあるか。
中学生のときには、こういった問題に対して
りんご4個、みかん0個、バナナ0個
りんご3個、みかん1個、バナナ0個 …
といった感じで書き出しながら場合の数を求めました。
しかし、高校が学習してきた知識を使うと、こういった面倒な問題が簡単に計算できるようになります。
では、その考え方について解説を進めていきます。
「重複を許して,4個取り出す」ということで、
まずは4個の〇を用意します。
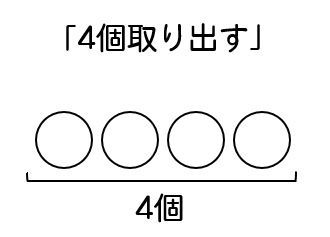
次に、これらをりんご、みかん、バナナの3種類に分類していきます。
3種類に分けるために、仕切りが2つ必要になります。

もしも、5種類に分けるのであれば、仕切りは \(5-1=4\)種類
\(n\)種類に分けるのであれば、仕切りは \((n-1)\)種類 となります。
種類数から1を引いた数が必要な仕切りの数ですね。
そして、〇と仕切りを用意できたら、これらの並べ方を考えていきましょう。
〇と仕切りを並べかえたとき、最初の仕切りより左にある〇をりんご、仕切りと仕切りの間にある〇をみかん、最後の仕切りより右にある〇をバナナとして考えていきます。

すると、問題で与えられている場合の数は、〇4個と仕切り2個の並べ方の総数と等しくなるってことが分かりますね。
よって、並べ方の総数は次のように計算することができるので、
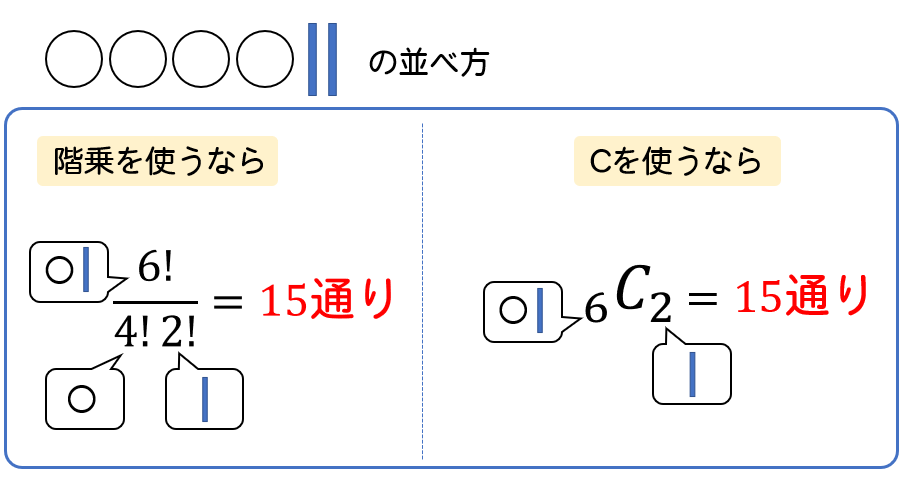
答えは、15通りとなります。
階乗、Cを使った計算方法がありますが、どちらを使っても構いません。
個人的にはCを使ったほうが式がスッキリするので好きかなって思いますw
なんで、こんな計算方法なの?という方は、
こちらの記事で復習しておいてくださいね。
このように、重複を許す組み合わせを考える場合には、〇と仕切りの並べ方を利用すれば簡単に求めることができますね。
Hを使った公式
前の章で述べた通り、重複組み合わせでは〇と仕切りを使って考えるとラクに計算ができます。
⇒ 〇4個、仕切り \(3-1=2\)個 の計6個の並べ方を考える。
⇒ \(\frac{6!}{4!2!}\) または \(_{6}C_{4}\)
\(n\)種類のモノを\(r\)個取り出す。
⇒ 〇\(r\)個、仕切り \((n-1)\)個 の計 \((n+r-1)\)個の並べ方を考える。
⇒ \(\frac{(n+r-1)!}{r!(n-1)!}\) または \(_{n+r-1}C_{r}\)
こんな感じで計算していけばOKです。
最初のうちは、イメージ図として〇と仕切りを書きながら考えるとイイですが、慣れてくると「何種類」「何個取り出す」の文章を読んだだけで式が作れるようになってきます。
そこで!
この計算方法を「H」という記号を使って、公式化したものがあります。
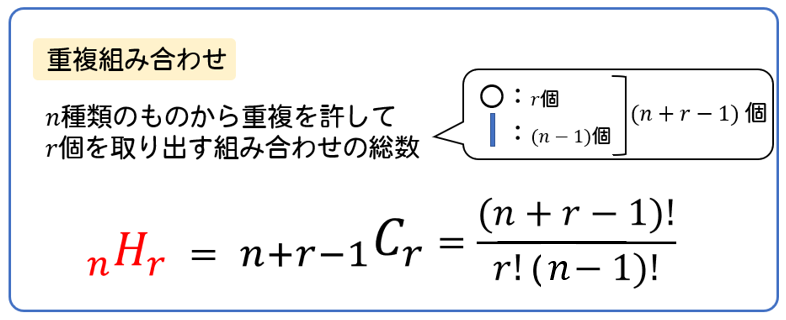

〇と仕切りの考え方ができる人にとっては、別に覚えていなくでも大丈夫な公式です。
ですが、記述問題でこの問題を解くときに…
「〇が何個で、仕切りが何個だから…」と書くのが面倒になります(^^;)
そこで、このHを使った公式を覚えておけば、
「3種類から重複を許して4個を取り出すので、\(_{3}H_{4}\)を計算すればよい」
とだけ記述すればよくなり、記述量を減らしてコンパクトな解答を作成することができます。
そういう意味で、問題を解くために「H」を覚えるというよりも、記述をラクにするために覚えるってのがおススメです。
では、次の章でいろんなパターンの例題を通して理解を深めておきましょう!
重複を許す組み合わせのいろんなパターン
重複組み合わせ【基本】
【問題】
\(1,2,3,4\) の4個の数字から重複を許して3個の数字を取り出す組み合わせは全部で何個あるか。
4種類から3個を取り出すので、
〇3個、仕切り \(4-1=3\)個となります。
$$\begin{eqnarray}_{6}C_{3}=20通り\end{eqnarray}$$
答え
$$20通り$$
【問題】
\((x+y+z)^5\) の展開式の異なる項の数を求めよ。
これは、\(x,y,z\) の3種類の文字から重複を許して5個の文字を取り出す組み合わせの総数と等しくなります。
よって、〇5個、仕切り\(3-1=2\)個と考えればよいので
$$\begin{eqnarray}_{7}C_{2}=21個\end{eqnarray}$$
答え
$$21個$$
1個以上を取る重複組み合わせ
【問題】
A,B,C,Dの4種類の商品を合わせて10個買うものとする。どの商品も少なくとも1個買うとき,買い方は全部で何通りあるか。
どの商品も1個以上買うという場合には、単純に〇と仕切りで今まで通りに計算できなくなります。
今までのやり方だと、仕切りが隣どうしになってしまって0個になる場合を含んでしまうからです。
そこで、最初にA,B,C,Dを1個ずつ取り除いてから考えるという方法があります。
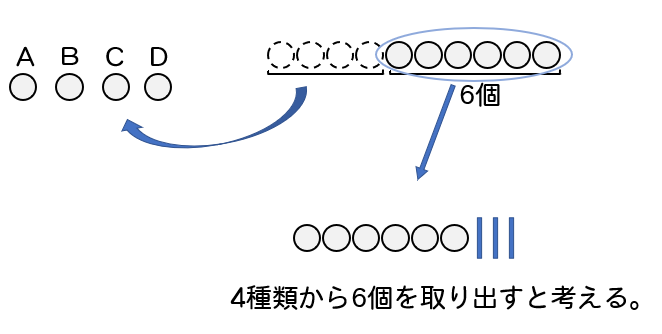
最初に1個ずつ配布しておいて、残った6個をどのように分類するかを考えていけばよいです。
そうすれば、これまで通り〇と仕切りを使って計算することができるようになります。
よって、
$$\begin{eqnarray}_{9}C_{3}=84通り\end{eqnarray}$$
答え
$$84通り$$
また、次のような考え方もOKです。

仕切りが隣どうし、または両端にくると0が発生してしまいます。
それを避けるために、〇のスキマに仕切りを入れる方法が何通りあるかを考えるというものです。
整数解の個数
【問題】
\(x+y+z=7\) ,\(x≧0\),\(y≧0\),\(z≧0\) を満たす整数の組 \((x,y,z)\) は何組あるか。
パッと見では難しそうに見えますが、これまでの重複組み合わせを用いると簡単に求めることができます。
\(x,y,z\) をすべて合わせると7になるということから、
〇を7個、仕切りを2個として並べ替えを考えればOKです。
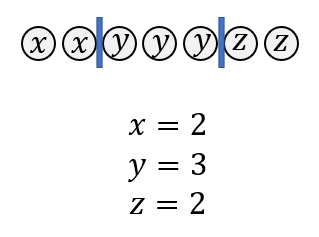
よって、
$$\begin{eqnarray}_{9}C_{2}=36組\end{eqnarray}$$
答え
$$36組$$
【問題】
\(x+y+z=7\) を満たす正の整数の組 \((x,y,z)\) は何組あるか。
こちらの問題では、「正」であることから \(x,y,z\) はいずれも1以上となります。
よって、「1個以上をとる重複組み合わせ」の考え方を利用していきましょう。
まずは、\(x,y,z\) に1個ずつ与えておく。
そして、残り4個の分類を考えていきます。
3種類から4個を取り出すことになるので、〇は4個、仕切りは2個となります。
よって、
$$\begin{eqnarray}_{6}C_{2}=15組\end{eqnarray}$$
答え
$$15組$$
まとめ!
お疲れ様でした!
仕切りを使った考え方について理解してもらえましたか?
テストや入試によく出題されるタイプの問題なので、何度も練習して理解を深めておいてくださいね!
また、記述をラクにするために「H」を活用することもおススメします。
慣れるまでは大変ですが、利用できるようにしておくとラクになりますので(^^)

- 倍数の個数を求める問題、どうやって考えればいい??
- 集合の要素の個数の問題「できた・できない・どちらも~」
- 集合の要素の個数の最大・最小を求める!イメージ図と不等式を使って考える!
- 3つの集合の要素の個数、イメージ図を使いながら求め方を解説!
- 展開したときの項の数を求め方は?
- 約数の個数と総和を求める公式は?問題を使って解説!
- 硬貨を使って支払える金額は何通り??
- 大中小3つのサイコロを投げるとき何通り?奇数、偶数?4の倍数?
- 順列Pの計算のやり方を簡単にサクッと解説するぞ!
- 3桁、4桁の整数をつくる問題をパターン別に解説!
- 円順列!交互、隣り合う、向かい合うときにはどう考える??
- じゅず順列の解き方はどうやる?円順列との違いは?
- 重複順列の基本問題の解き方をイチから解説するぞ!
- 部分集合の個数の求め方についてイチから解説するぞ!
- 部屋割りの考え方についてイチから解説!
- 平面、空間の塗り分け問題の解き方まとめ!
- 組み合わせCの計算のやり方を簡単にサクッと解説するぞ!
- 平行四辺形は何個ある?考え方を解説!
- 組み分けの場合の数の求め方・考え方をイチから解説!
- なぜ?同じものを含む順列の公式と使い方について問題解説!
- 重複を許す組み合わせ!Hを使った公式、仕切りを使った考え方を解説! ←今回の記事
- サイコロの最大値が5、最小値が2になる確率はどうやって考える?
- 反復試行の確率!なぜこんな公式に?Cを使う理由とは
- 反復試行の確率!3つの事象があるときのやり方は?
- 反復試行の確率!数直線、点の移動を考えるサイコロ問題の解き方は?
- 条件付き確率の考え方を図を使ってイチからわかりやすく!
- 期待値とは?求め方を簡単にサクッと解説!


















【Hを使った公式】の序盤
「3種類のモノを4個取り出す。
⇒ 〇4個、仕切り 4−1=3個 の計7個の並べ方を考える。
⇒ 7!/(4!3!) または 7C3」
は、「仕切り3-1=2個の計6個の並べ方を考える。」じゃないかな
訂正しておきました!
ご指摘ありがとうございますm(__)m
nHr=n+r-1Cr=(分数)の分母はr!(n-1)!ではないですか?
ミスってました!
訂正しておきました。
ありがとうございます!!