【順列】3桁、4桁の整数をつくる問題をパターン別に解説！

高校数学Aで学習する場合の数の単元から

「3桁、4桁の整数をつくる場合の数」

についてパターン別に解説していきます。

 

取り上げる問題はこちら！

 

倍数の判定方法を覚えておこう！

整数をつくる問題では、倍数の判定方法を覚えておく必要があります。

以下にまとめておくので、問題を解くための知識として頭に入れておきましょう。

偶数（2の倍数）	一の位が偶数\(（0,2,4,6,8）\)
奇数	一の位が奇数数\(（1,3,5,7,9）\)
3の倍数	各位の数の和が3の倍数
4の倍数	下2桁が4の倍数
5の倍数	一の位が0または5
6の倍数	2の倍数 かつ 3の倍数 （各位の和が3の倍数であり，一の位が偶数）
9の倍数	各位の数の和が9の倍数

 

問題①（0を含まないパターン）

6個の整数 \(1\), \(2\), \(3\), \(4\), \(5\), \(6\) から異なる3個の数字を選んで3桁の整数をつくるとき，次のような数の個数を求めよ。

（1）すべての整数

整数をつくる場合には、各位のマスを作って、そこに何通りの数を入れることができるかを考えるとよいです。

百の位は、1～6の数を入れることができるので6通り。

十の位は、百の位で使った数以外を入れることができるので5通り。

一の位は、百、十の位で使った数以外を入れることができるので4通り。

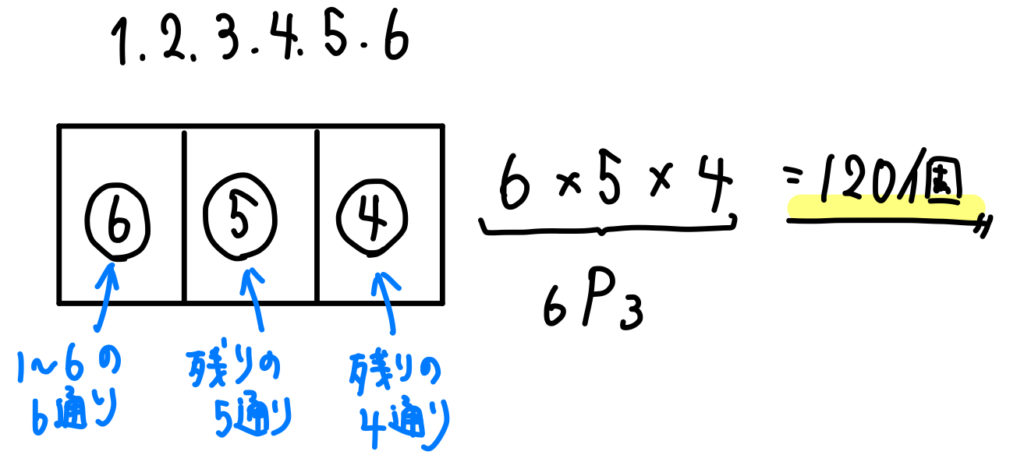
よって、このように計算することができます。

簡単ですね(/・ω・)/

6つの数から3つを並べると考えることもできるので、順列を使って\({}_6 \mathrm{ P }_3\) と考えることもできます。

 

（2）偶数

偶数にするためには、一の位が偶数\(（2,4,6）\)になる必要があります。

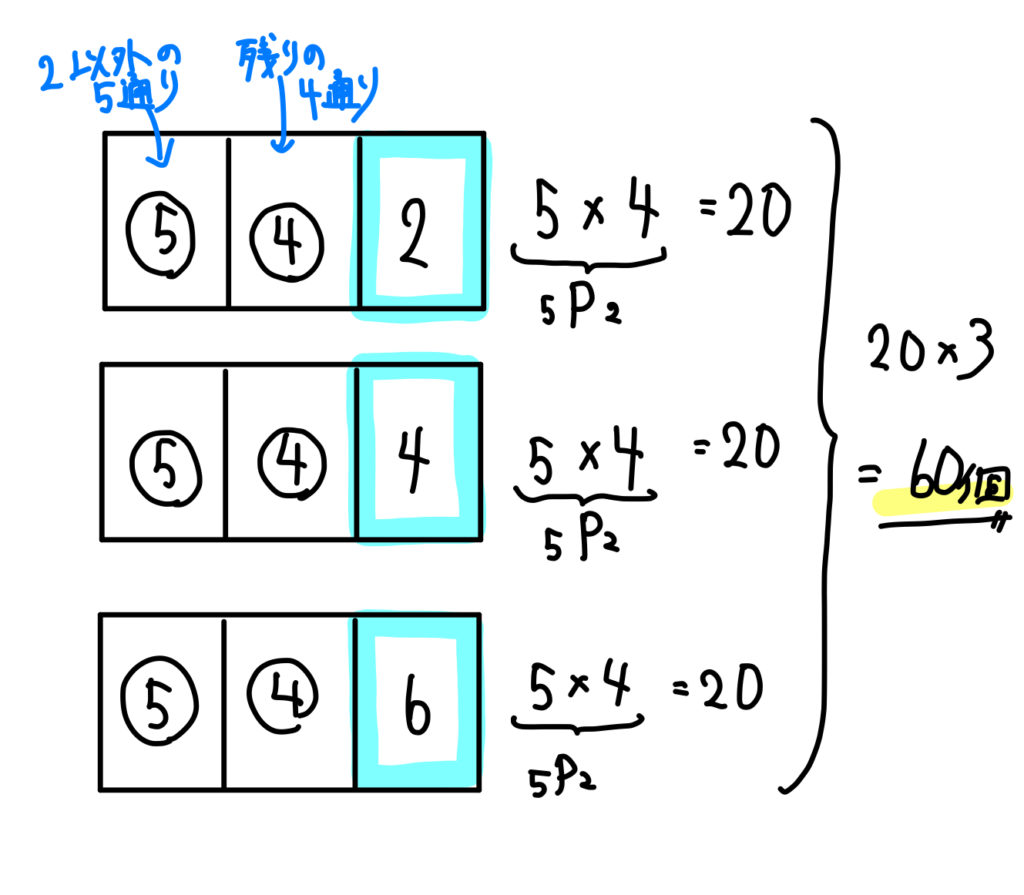
よって、このように一の位が2になるときは何通りできるか、一の位が4のときは…

と考えて、合計を求めていけばOKです。

 

一の位が2になるときは、

百の位に入れることができる数は、2以外の\(1,3,4,5,6\) の5通り。

十の位に入れることが出来る数は、2と百の位で使った数以外なので4通り。

以上より、\(5\times 4=20\) 個。

 

同様に、一の位が4，6の場合も考えると、

合計は、\(20\times 3=60\) 個となります。

 

 

（3）4の倍数

4の倍数になるためには、下2桁の数が4の倍数になる必要があります。

\(1\), \(2\), \(3\), \(4\), \(5\), \(6\)を使ってできる4の倍数は、

\(12,16,24,32,36,52,56,64\) の8パターンです。

 

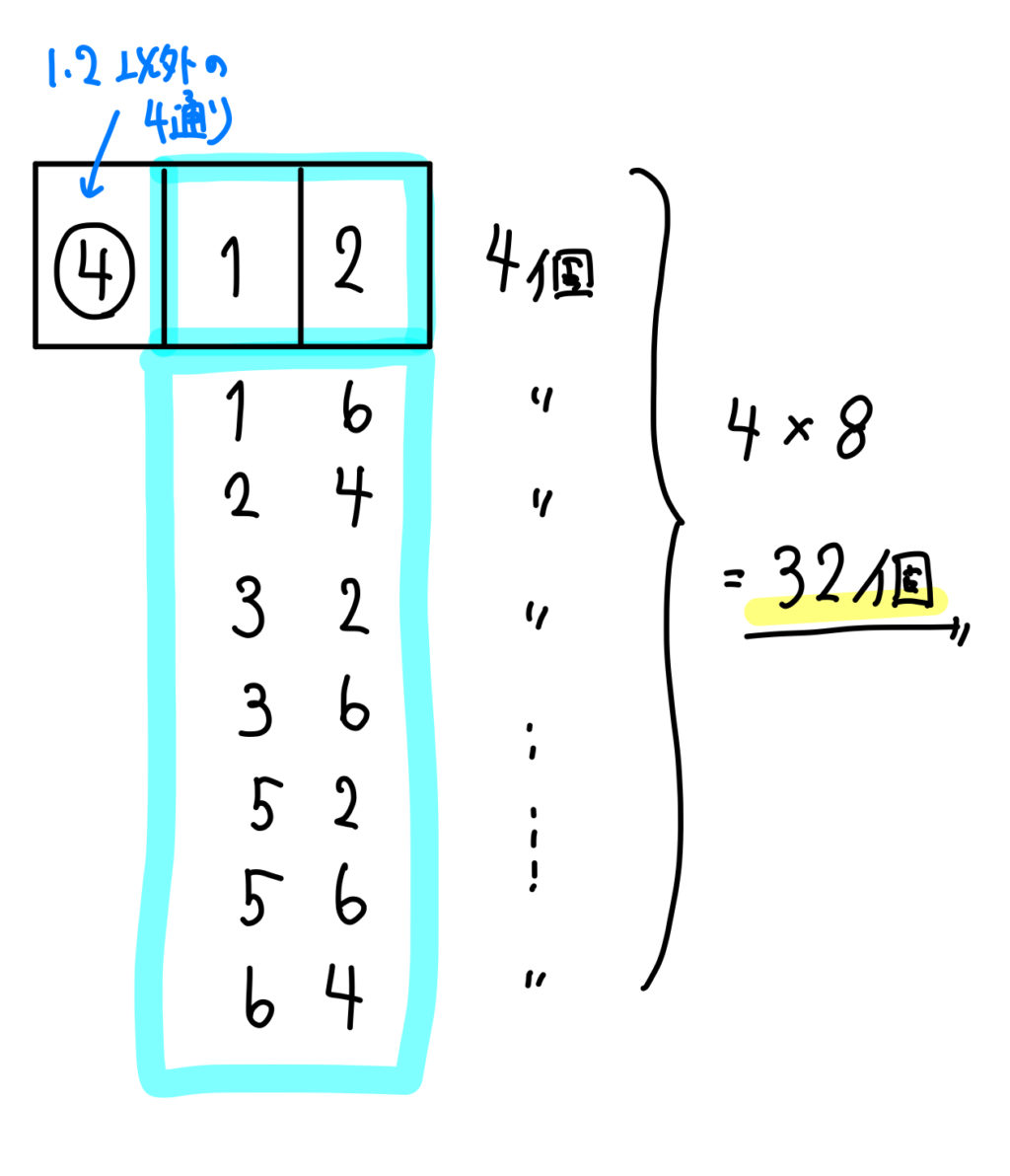
下2桁が12になるとき

百の位に入れることができる数は、\(1,2\) 以外の4通り。

他の場合も同様に考えることができるので、\(4\times 8=32\) 個となります。

 

（4）5の倍数

5の倍数となるには、一の位が0または5になる必要があります。

今回の問題では0になることはありませんので、一の位が5になるパターンのみ考えていきましょう。

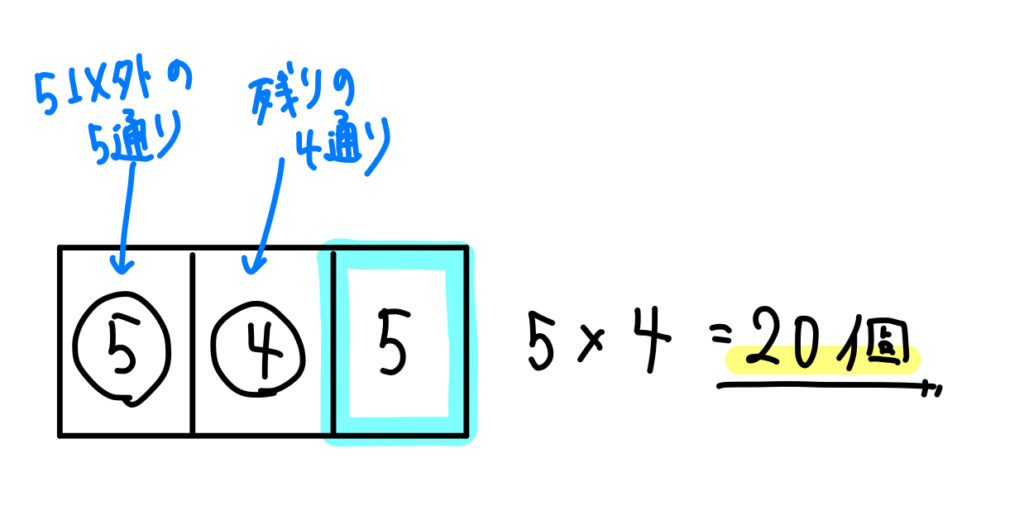
百の位に入れることができる数は、5以外の5通り。

十の位に入れることができる数は、5と百の位で使った数以外なので4通り。

よって、\(5\times 4=20\) 個となります。

 

 

問題②（0を含むパターン）

6個の整数 \(0\), \(1\), \(2\), \(3\), \(4\), \(5\) から異なる4個の数字を選んで4桁の整数をつくるとき，次のような数の個数を求めよ。

（1）すべての整数

使える数の中に「0」が含まれているときには注意が必要です。

最高位には0を入れることができないからです。

そのことを踏まえて、考えると次のようになります。

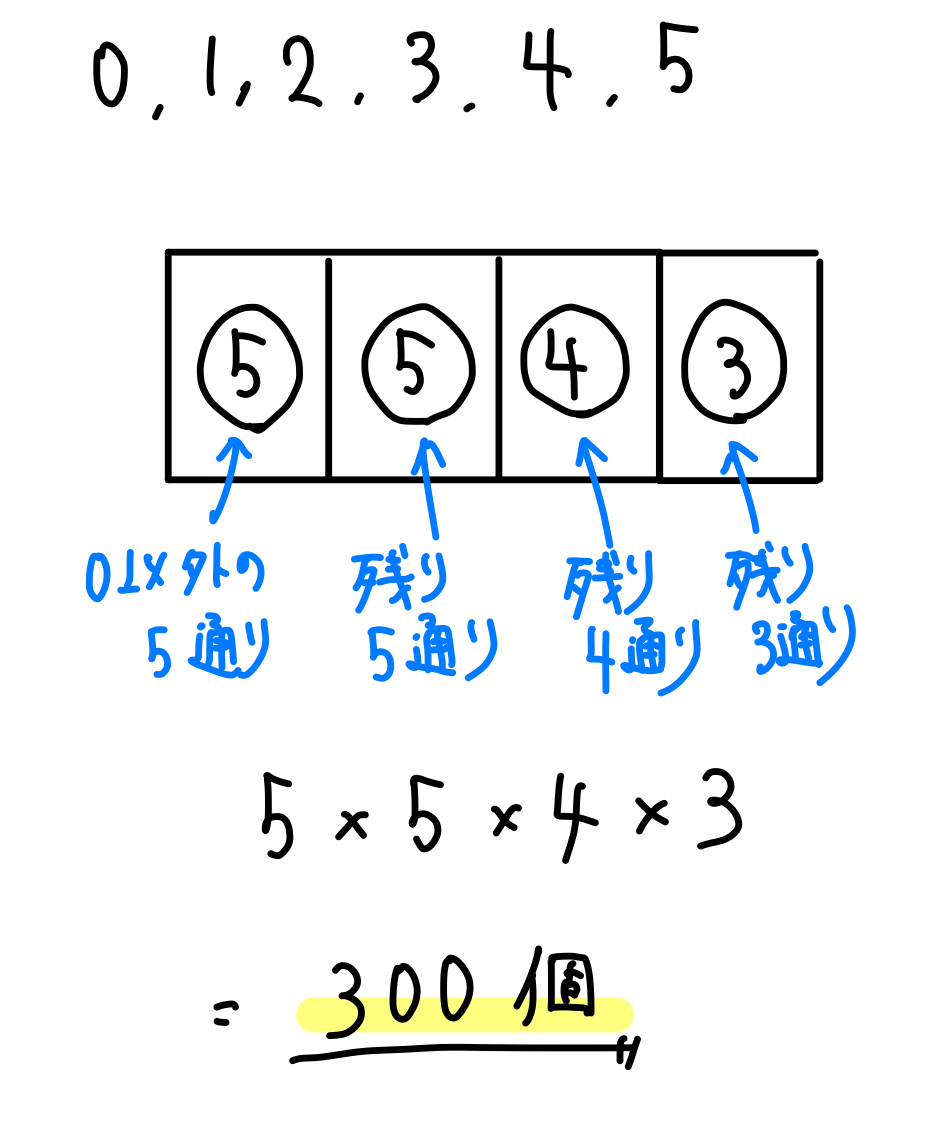
千の位には、0を入れることができないで「\(1,2,3,4,5\)」の5通り。

百の位には、0が復活し、千の位で使った数以外の5通り。

十の位には、千と百の位で使った数以外の4通り。

一の位には、千と百と十の位で使った数以外の3通り。

 

以上より、\(5\times 5\times 4\times 3=300\)個となります。

 

0が含まれているときには、最高位に入れることができる数が減ってしまうことに注意してくださいね。

（2）偶数

偶数になるためには、一の位が偶数（\(0,2,4\)）になる必要があります。

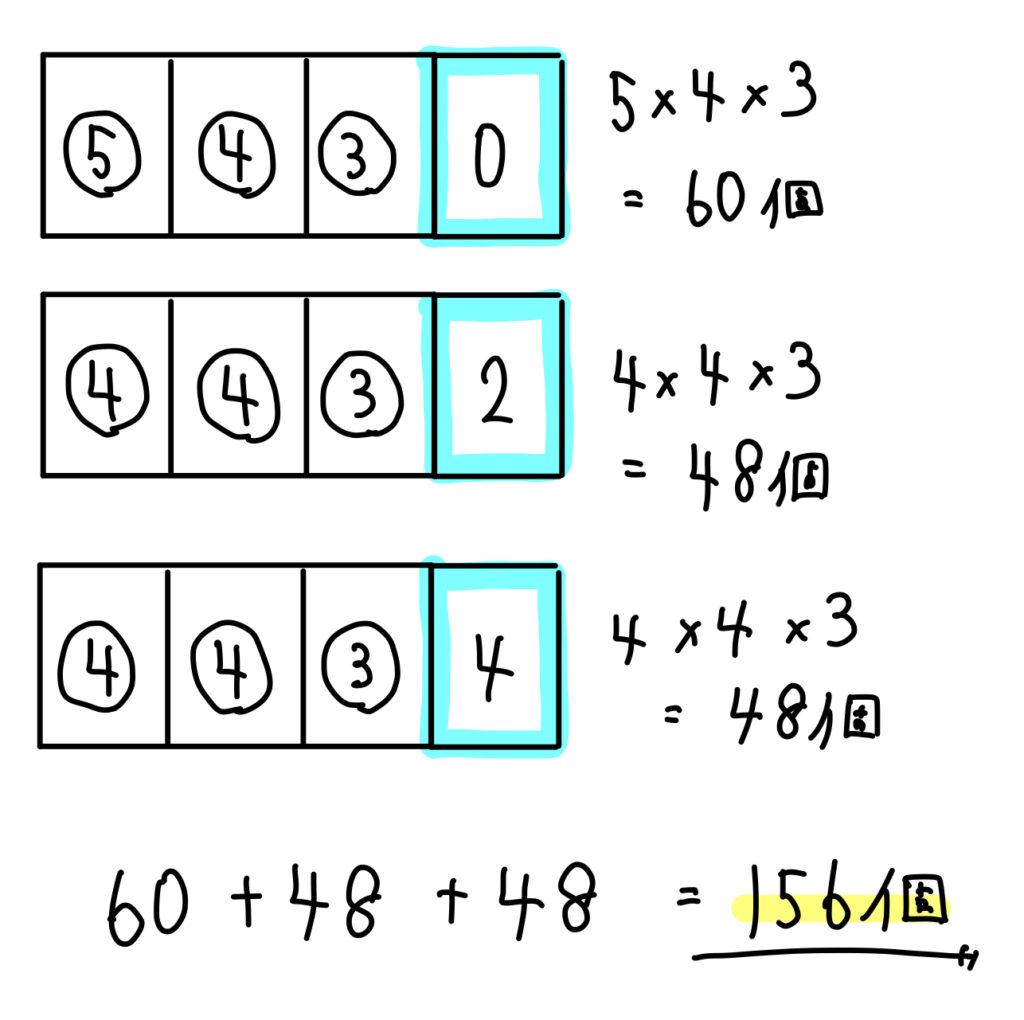
一の位が0になるとき

千の位は5通り、百の位は4通り、十の位は3通り　⇒　\(5\times 4\times 3=60\)個。

 

一の位が2になるとき

千の位は0，2以外の4通り、百の位は4通り、十の位は3通り　⇒　\(4\times 4\times 3=48\)個。

一の位が4になるときも同様に\(48\)個。

 

以上より、\(60+48+48=156\)個となります。

 

（3）3の倍数

3の倍数になるには、各位の数の和が3の倍数になる必要があります。

これがちょっとめんどうなんですが、地道にやっていきましょう(^^;)

 

まずは、 \(0\), \(1\), \(2\), \(3\), \(4\), \(5\) の数から合計が3の倍数となる数の組み合わせを見つけます。

すると、

\((0,1,2,3)\), \((0,1,3,5)\), \((0,2,3,4)\), \((0,3,4,5)\), \((1,2,4,5)\) の5パターンあることが分かります。

これを見つけるのがちょっと時間かかるかもしれませんが、がんばって見つけましょう！

 

\((0,1,2,3)\) を使ってできる4桁の整数は、

千の位は0以外の\(1,2,3\) の3通り。

百の位は千の位で使った数以外の3通り。

十の位は千と百の位で使った数以外の2通り。

一の位は残った最後の数を入れるので1通り。

よって、\(3\times 3\times 2\times 1=18\) 個。

0を含んでいる \((0,1,3,5)\), \((0,2,3,4)\), \((0,3,4,5)\) の3パターンも同様にそれぞれ18個できます。

 

\((1,2,4,5)\) を使ってできる4桁の整数は、

千の位は4通り。

百の位は千の位で使った数以外の3通り。

十の位は千と百の位で使った数以外の2通り。

一の位は残った最後の数を入れるので1通り。

よって、\(4\times 3\times 2\times 1=24\) 個。

 

以上より、\(18\times 4+24=96\)個。

 

 

3の倍数はちょっとめんどうですが、まずは和が3の倍数になる数の組み合わせを見つける。

そして、それらの数の並べ方を考えていくという流れになります。

（4）6の倍数

6の倍数は、2の倍数かつ3の倍数となります。

（3）の問題で3の倍数になる数を見つけていますので、その中から偶数になる数を探していきましょう。

 

3の倍数になるのは、\((0,1,2,3)\), \((0,1,3,5)\), \((0,2,3,4)\), \((0,3,4,5)\), \((1,2,4,5)\)

これらの数を使ってできる数になります。

この中から一の位が偶数（\(0,2,4\)）になるものを考えていきます。

 

一の位が0になるとき

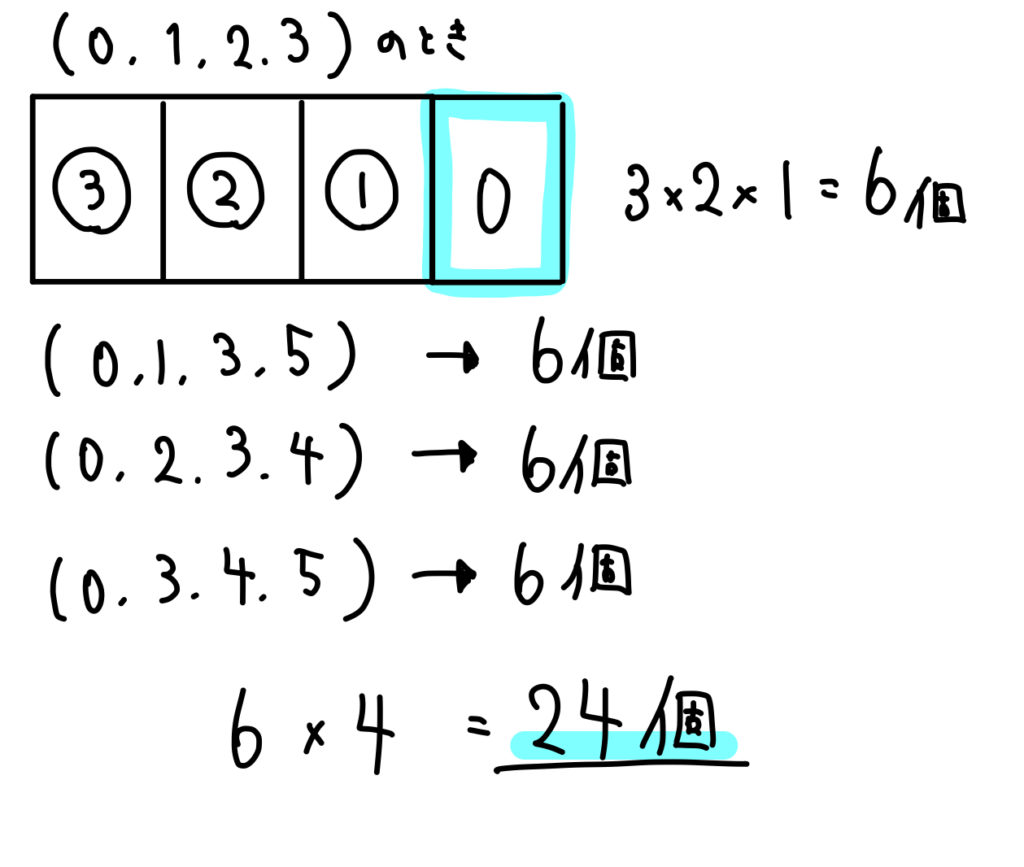
このように24個あることが分かります。

 

一の位が2になるとき

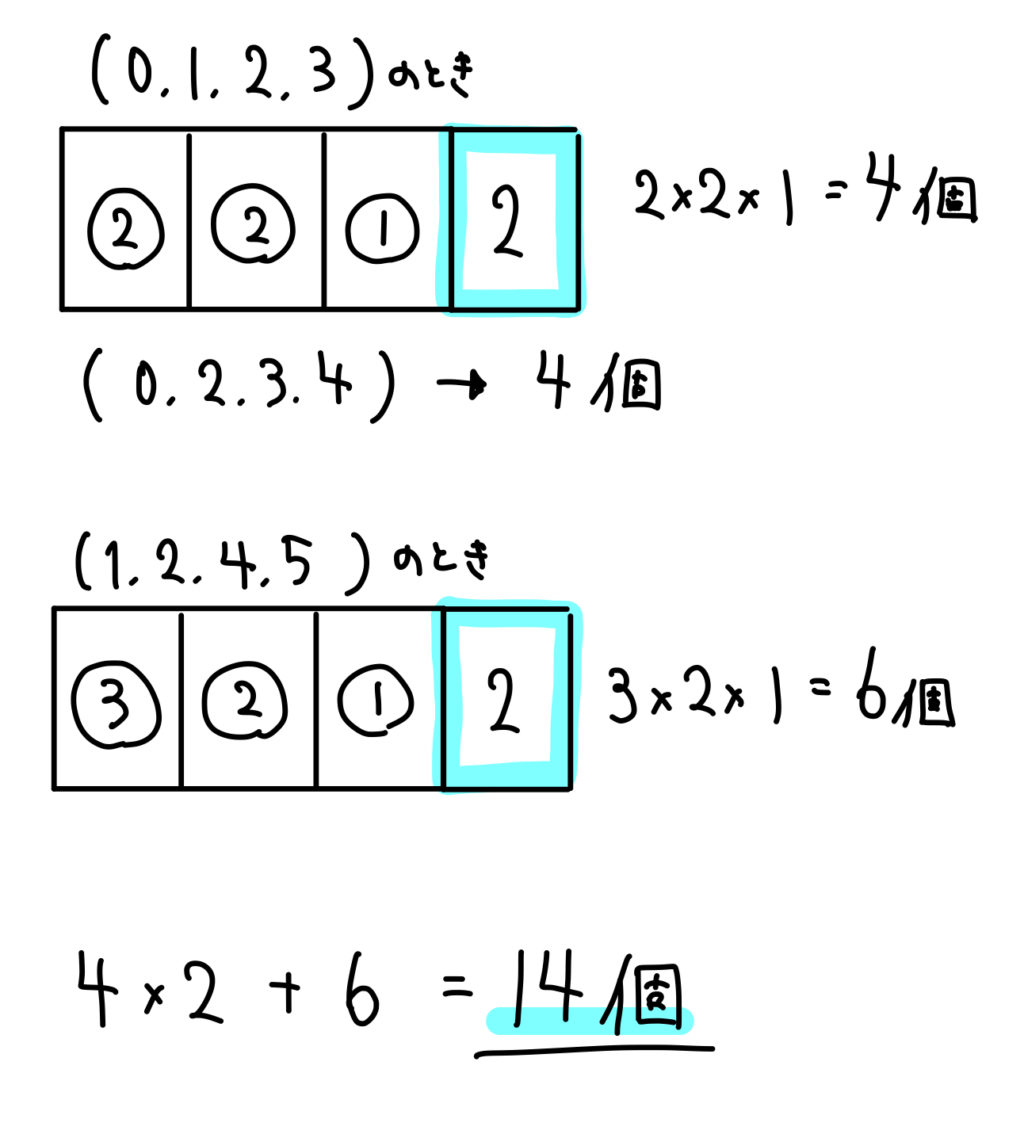
このように14個あることが分かります。

 

最後に、一の位が4になるときも同様に14個となりますので、

以上より、\(24+14+14=52\)個。

 

 

（5）2400より大きい整数

2400より大きくなる整数を考える場合

まずは、千の位に注目してみましょう。

千の位が3，4，5になるときには、下3桁がどんな数であっても2400より大きくなるので、

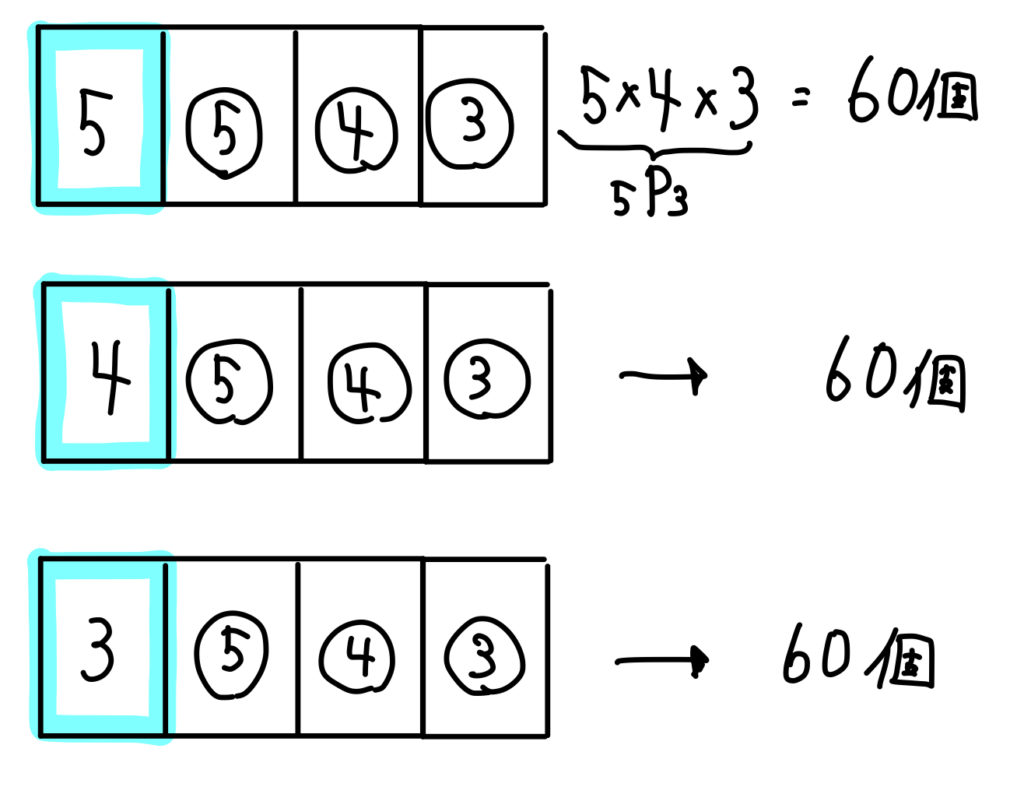
このように数えることができます。

 

そして、千の位が2のときには、百の位が4，5のときに限り2400よりも大きい整数となります。

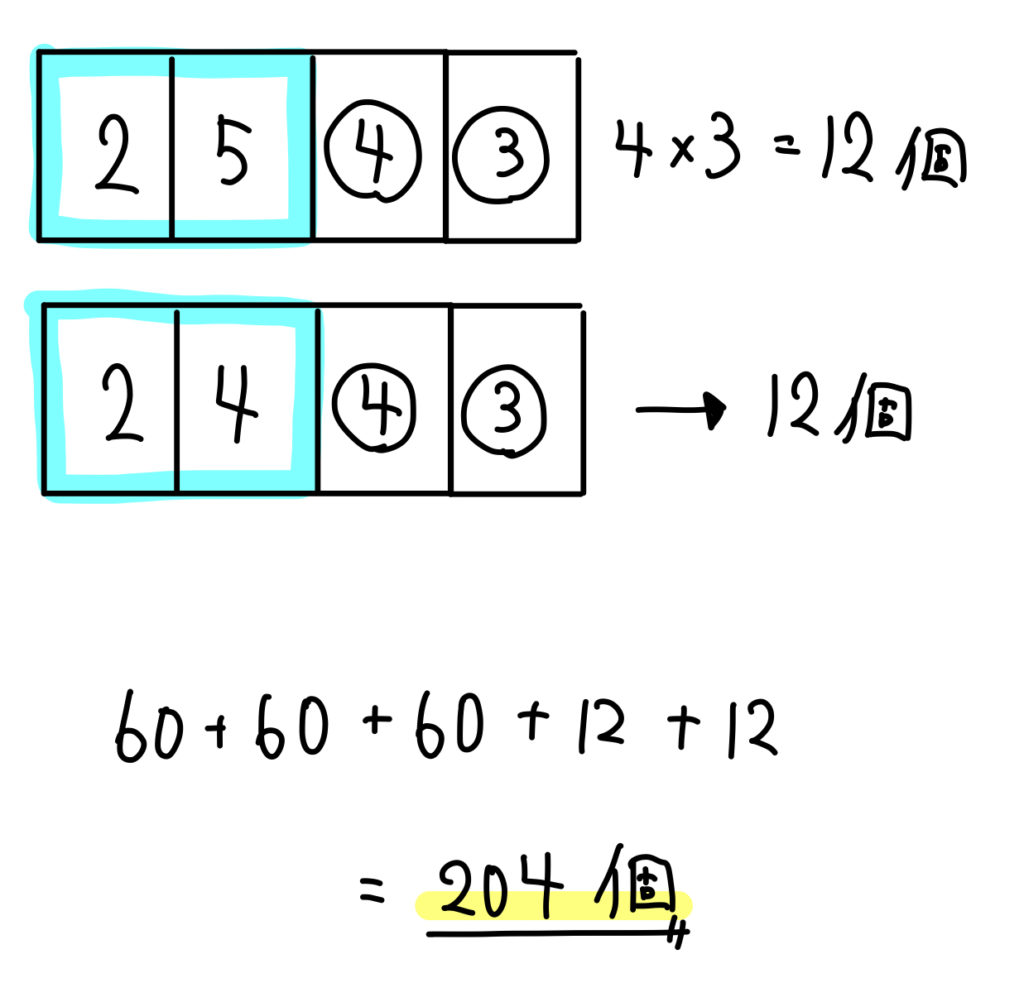
以上より、\(60+60+60+12+12=204\)個となります。

 

 

まとめ！

お疲れ様でした！

整数をつくる問題では、問題集の解説には\(P, !\)を使って式で表現されています。

ですが、それではちょっとイメージがしづらい…という方は、今回の記事で紹介したように桁数の分だけマスを作って考えてみるとよいですね。

 

また、3の倍数を考える問題はちょっとややこしい…教えてくださいと質問をいただくことも多いです。

和が3の倍数になる組み合わせを見つけること。

そして、それらの並び替えを考えること。

これは、たくさん練習問題を解いて慣れるようにしましょう！

 

 

成績を上げて、志望校合格を勝ち取りたい中3生の方！

数スタの無料メルマガ講座で合格を勝ち取りませんか？

今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！

数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！