高校数学Aで学習する場合の数の単元から
「組み分けの場合の数」
について解説していきます。
取り上げる問題はこちら！
【問題】
9人を次のように分ける方法は何通りあるか。
（1）4人，3人，2人の3組に分ける。
（2）3人ずつA，B，Cの3組に分ける。
（3）3人ずつ3組に分ける。
（4）5人，2人，2人の3組に分ける。
組み分けの問題では、
「分けるものが区別できるかどうか」
が大事なポイントとなります。
問題(1)(2) 区別できるパターン
9人を次のように分ける方法は何通りあるか。
（1）4人，3人，2人の3組に分ける。
4人、3人、2人という分け方は、分けるものに名前がついていませんが、人数が異なることから3組は区別できると判断します。
分けるものが区別できる場合は簡単！
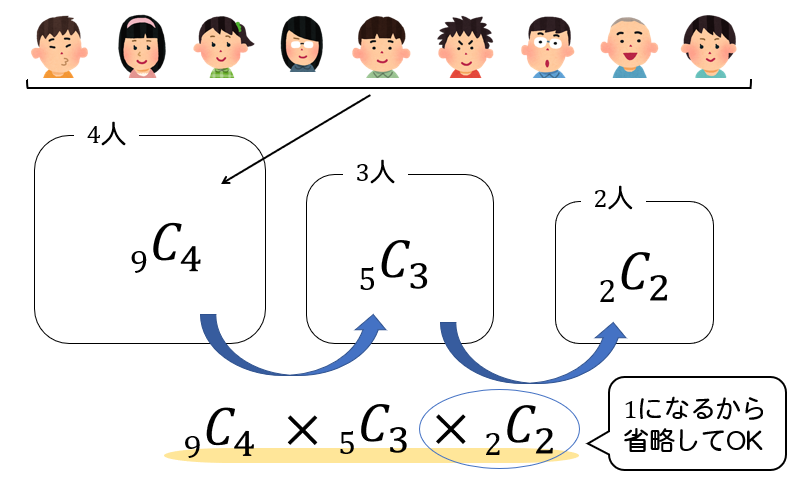
まず、9人の中から4人を選ぶ。 ⇒ \(_{9}C_{4}\)
次に残った5人の中から3人を選ぶ。 ⇒ \(_{5}C_{3}\)
そして、最後の2人の中から2人を選ぶ。 ⇒ \(_{2}C_{2}\)（必ず1通りになるので省略してOK）
よって、
$$\begin{eqnarray}&&_{9}C_{4}\times _{5}C_{3}\times _{2}C_{2}\\[5pt]&=&\frac{9\cdot 8\cdot 7\cdot 6}{4\cdot 3\cdot 2\cdot 1} \times \frac{5\cdot 4}{2\cdot 1}\times 1\\[5pt]&=&1260通り\cdots (解)\end{eqnarray}$$
となります。
答え
$$(1) 1260通り$$
今度の分け方は、人数が同じになっていますが、組に名前がついていることから3組は区別できると判断します。
組が区別できる場合には、Cを使って順に計算していけばOKです。
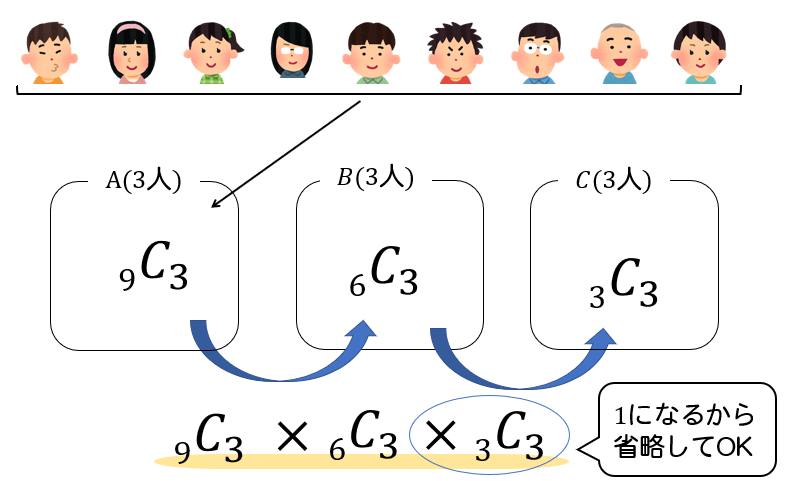
まず、9人の中から3人を選ぶ。 ⇒ \(_{9}C_{3}\)
次に残った6人の中から3人を選ぶ。 ⇒ \(_{6}C_{3}\)
そして、最後の3人の中から3人を選ぶ。 ⇒ \(_{3}C_{3}\)（必ず1通りになるので省略してOK）
よって、
$$\begin{eqnarray}&&_{9}C_{3}\times _{6}C_{3}\times _{3}C_{3}\\[5pt]&=&\frac{9\cdot 8\cdot 7}{3\cdot 2\cdot 1} \times \frac{6\cdot 5\cdot 4}{3\cdot 2\cdot 1}\times 1\\[5pt]&=&1680通り\cdots (解)\end{eqnarray}$$
となります。
答え
$$(2) 1680通り$$
ポイント！
人数が違う、組に名前がついているなど
分ける組が区別できる場合、\(C\)を使って計算を進めていく。
問題(3)(4) 区別できないパターン
9人を次のように分ける方法は何通りあるか。
（3）3人ずつ3組に分ける。
分ける組の人数が同じ、組に名前がついていないことから、3組は区別ができないと判断します。
分ける組に区別ができないとき、区別ができるときには次のような関係があります。
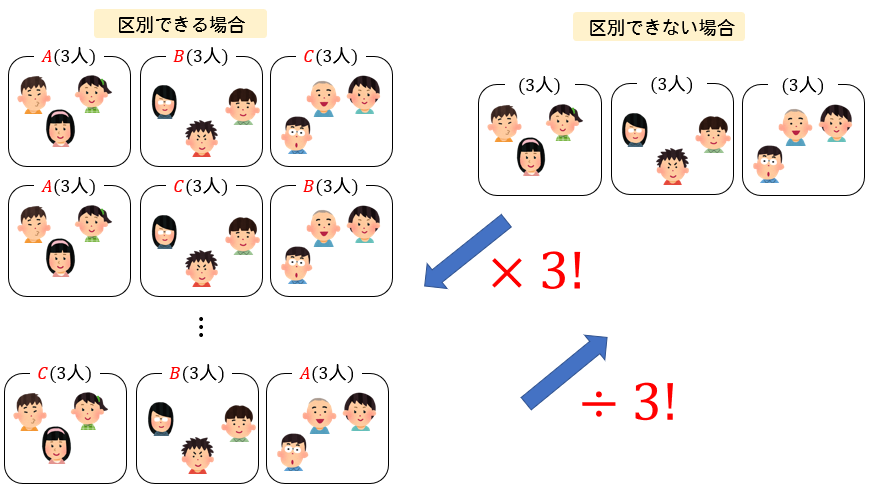
区別できないときには、3人ずつに分けたら終わりです。
一方で区別ができるときには、3人ずつに分けた後、どの組み入れるかまで考えます。
よって、区別できないときの1通りに対して、区別できるときには A,B,Cの順列 \(3!\) 分だけあるということになります。
逆に考えると、区別できないときは、区別できるときの場合の数を \(\div 3!\) すれば求めることができるということになりますね。
区別できる場合は、Cを使って簡単に計算することができますので、
- 区別できる場合を求める。
- 区別できない組の数の階乗で割る。
- 区別できない場合の数が求まる。
よって、求める場合の数は
$$\begin{eqnarray}&&\frac{_{9}C_{3}\times _{6}C_{3}\times _{3}C_{3}}{3!}\\[5pt]&=&\frac{1680}{6}\\[5pt]&=&280通り\cdots (解)\end{eqnarray}$$
となります。
答え
$$(3) 280通り$$
5人，2人，2人の中で区別ができないのは「2人，2人」の2組だけです。
よって、次のように求めることができます。
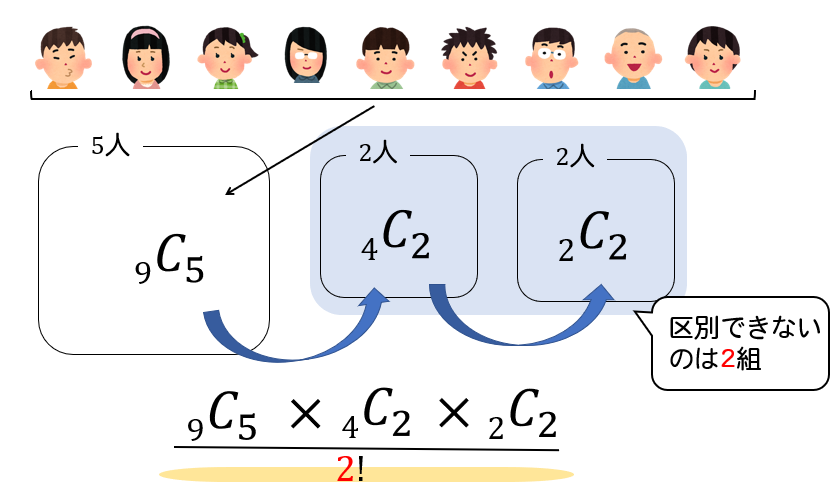
$$\begin{eqnarray}&&\frac{_{9}C_{5}\times _{4}C_{2}\times _{2}C_{2}}{2!}\\[5pt]&=&\frac{9\cdot 8\cdot 7\cdot 6}{4\cdot3\cdot 2\cdot 1} \times \frac{4\cdot 3}{2\cdot 1}\times \frac{1}{2}\\[5pt]&=&378通り\cdots (解)\end{eqnarray}$$
となります。
答え
$$(4) 378通り$$
ポイント！
分ける組が区別できないときは、
区別できるときの場合の数を求めて、区別できない組の数の階乗で割る。
練習問題に挑戦！
【問題】
10冊の異なる本を次のように分ける方法は何通りあるか。
（1）5冊，3冊，2冊の3組に分ける。
（2）5冊ずつA，Bの2組に分ける。
（3）5冊ずつ2組に分ける。
（4）4冊，3冊，3冊の3組に分ける。
まとめ！
お疲れ様でした！
組み分けの問題はテストや入試で出題されやすいので、とっても重要ですね。
ポイントとしては、冒頭でも述べた通り「区別できるか、できないか」
区別できる場合は、Cでそのまま計算。
区別できない場合は、できる場合に比べて数が減ってしまいます。
そのため、区別できない組の数の階乗で割ってあげるようにしましょう。
この考え方が身についていれば、組み分けの問題は簡単です。
サクッと得点しちゃいましょう(/・ω・)/
コメントを残す