【苦手な人向け】組み合わせCの計算のやり方を簡単にサクッと解説するぞ！

今回の記事では高校数学Aで学習する

「組み合わせCの計算のやり方」

についてイチから解説していくよ。

この記事を通して、次のようなCの計算ができるようになろう！

【問題】次の値を計算しなさい。

（1）${}_7 \mathrm{ C }_3$

（2）${}_4 \mathrm{ C }_4$

（3）${}_5 \mathrm{ C }_0$

（4）${}_{10} \mathrm{ C }_8$

（5）${}_n \mathrm{ C }_3$

そして、組み合わせCが表している意味についても理解しておこう！

Cの計算をサクッと学びたい方は、こちらの動画をどうぞ！

組み合わせCを使った文章題の解説はこちら！

動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします＾＾

高校メルマガ講座の無料登録はこちら！

Contents

組み合わせCの計算のやり方
組み合わせCの意味、どんな場面で使える？？
PとCの違いは？？
組み合わせCを使った文章題にチャレンジ！
まとめ！

組み合わせCの計算のやり方

組み合わせCの計算のやり方についてサクッと理解しておきましょう。

組み合わせの計算では、順列Pの知識を利用します。

⇒ 順列Pの計算のやり方を簡単にサクッと解説するぞ！

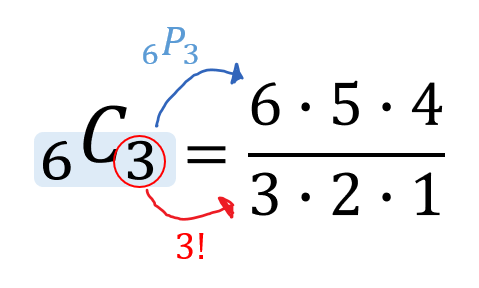
左と右の数を使ってPの計算をします。

そして、右の数の階乗で割ってあげれば完成となります。

上の式であれば「６シー３」と読みます。

組み合わせCの基本計算

では、次の問題でやり方を確認しておきましょう。

【問題】次の値を計算しなさい。

（1）${}_7 \mathrm{ C }_3$

（2）${}_4 \mathrm{ C }_4$

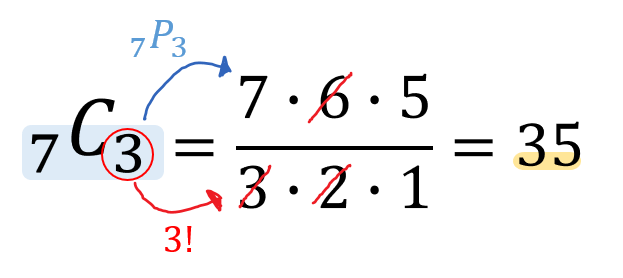
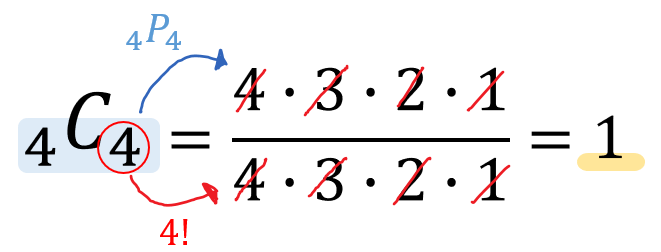
Cの計算では分数の形が出てきます。

約分などをミスしないよう、ていねいに途中式を書くことが大切です。

それと、（2）の問題から分かるように左と右の数が同じになる場合

${}_3 \mathrm{ C }_3$、${}_9 \mathrm{ C }_9$など

これらは分母と分子がすべて同じ数になるので、計算をすると必ず1になってしまいます。

覚えておきたい0の計算

0が含まれている場合にはどうなるのでしょうか。

このように0が含まれている場合には1になります。

まぁそういうもんなんだなってことで覚えておいてくださいな。

ってことは次の問題は楽勝で解けちゃいますね！

【問題】次の値を計算しなさい。

（3）${}_5 \mathrm{ C }_0$

0が含まれているので、計算することなく1になるってことが分かります。

$${}_5 \mathrm{ C }_0=1\cdots(解)$$

小さい数に変換して考える組み合わせ

【問題】次の値を計算しなさい。

（4）${}_{10} \mathrm{ C }_8$

10に8！？

げげっ…計算が大変そうだなぁ

って思ったよね(^^;)

だけど、Cの計算には次のような性質があります。

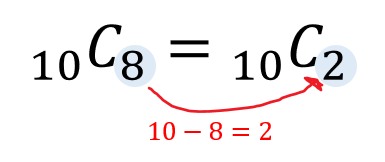
${}_{10} \mathrm{ C }_8$と${}_{10} \mathrm{ C }_2$は同じ値になるのです。

【例】

$${}_{10} \mathrm{ C }_7={}_{10} \mathrm{ C }_3$$

$${}_{20} \mathrm{ C }_{18}={}_{20} \mathrm{ C }_2$$

$${}_{100} \mathrm{ C }_{99}={}_{100} \mathrm{ C }_1$$

同じ値が出るんだったら、なるべく計算がラクな方がいいに決まってるよね！

というわけで、右に大きな数が出てきたときには、数を小さく変換してから計算するようにしてみましょう。

$$\begin{eqnarray}{}_{10} \mathrm{ C }_8&=&{}_{10} \mathrm{ C }_2\\[5pt]&=&\frac{10\cdot 9}{2\cdot 1}\\[5pt]&=&45\cdots(解) \end{eqnarray}$$

nを含む組み合わせCの計算

【問題】次の値を計算しなさい。

（5）${}_n \mathrm{ C }_3$

文字が含まれていても落ち着いて基本通りに計算していきましょう！

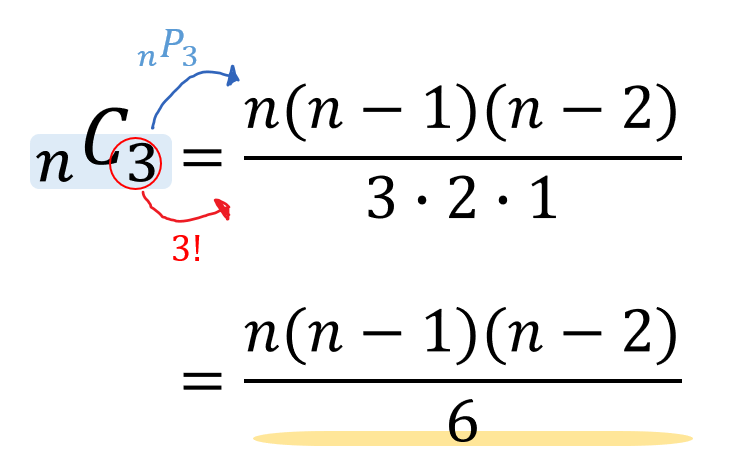
あれ、${}_n \mathrm{ P }_3$ってどうだっけ…？という方は

⇒ 順列Pの計算のやり方を簡単にサクッと解説するぞ！

こちらの記事で確認しておきましょう。

練習問題に挑戦

次の計算をしなさい。

（1）${}_8 \mathrm{ C }_3$

解説＆答えはこちら

答え

$$56$$

$${}_8 \mathrm{ C }_3=\frac{8\cdot 7\cdot 6}{3\cdot 2\cdot 1}=56$$

次の計算をしなさい。

（2）${}_9 \mathrm{ C }_0$

解説＆答えはこちら

答え

$$1$$

$${}_9 \mathrm{ C }_0=1$$

0が含まれているときには計算せずに1でしたね。

次の計算をしなさい。

（3）${}_{12} \mathrm{ C }_{10}$

解説＆答えはこちら

答え

$$66$$

$$\begin{eqnarray}{}_{12} \mathrm{ C }_{10}&=&{}_{12} \mathrm{ C }_{2}\\[5pt]&=&\frac{12\cdot 11}{2\cdot 1} \\[5pt]&=&66\end{eqnarray}$$

右の数が大きいときには変換をしてから計算するようにしましょう。

次の計算をしなさい。

（4）${}_{n} \mathrm{ C }_{2}$

解説＆答えはこちら

答え

$$\frac{n(n-1)}{2}$$

$$\begin{eqnarray}{}_{n} \mathrm{ C }_{2}&=&\frac{n(n-1)}{2\cdot 1} \\[5pt]&=&\frac{n(n-1)}{2}\end{eqnarray}$$

組み合わせCの意味、どんな場面で使える？？

さて、ここまでは組み合わせCの計算方法について解説をしてきました。

計算はできるようになったとはいえ

どういった場面で使えるのかを理解しておかないと意味がありませんね。

というわけで、組み合わせCの意味についてサクッと解説しておきます。

${}_6 \mathrm{ C }_3$というのは

「6個から3個を取り出す組み合わせは何通りあるか」

を表しているものになります。

組み合わせとは、どんなペアができるか？っていうものですね。

そして、上で紹介してきた計算方法によって

これが何通りあるのかを計算することができるというわけです。

7個から4個を取り出す組み合わせは何通りある？

っていうのは、Cを使って表すと${}_7 \mathrm{ C }_4$となります。

文章で書くと長いけど、Cを使って表すとスッキリと短く表せますね。

そういった意味でCはとても便利な記号ってわけです。

では、組み合わせCを用いる文章題をちょっとだけ確認しておきましょう。

【問題】

8人の生徒から3人を選らぶのは何通りか。

「8人の中から3人を選ぶ」

ということだから、Cを使うと${}_8 \mathrm{ C }_3$となりますね。

あとは計算あるのみです。

$${}_8 \mathrm{ C }_3=\frac{8\cdot 7\cdot 6}{3\cdot 2\cdot 1}=56通り\cdots(解)$$

PとCの違いは？？

さて、最後に順列Pと組み合わせCの違いについて確認しておきましょう。

順列Pとは、選んだあとに並べたもの、順番を考えている。

組み合わせCとは、選んだもの、選んだだけで終わり。

という違いがあります。

順番を考えるなら順列P

選んで終わりなら組み合わせC

と考えておけばよいですね。

組み合わせCを使った文章題にチャレンジ！

ここからはもうちょっと踏み込んで、テストの点数をUPさせたい方にむけて演習問題を用意しました。

【問題】

男子3人、女子5人の中から、4人を選んで組を作るとき、次のような組は何通りあるか求めなさい。

（1）男子2人と女子2人が選ばれる

（2）男子が少なくとも1人は選ばれる

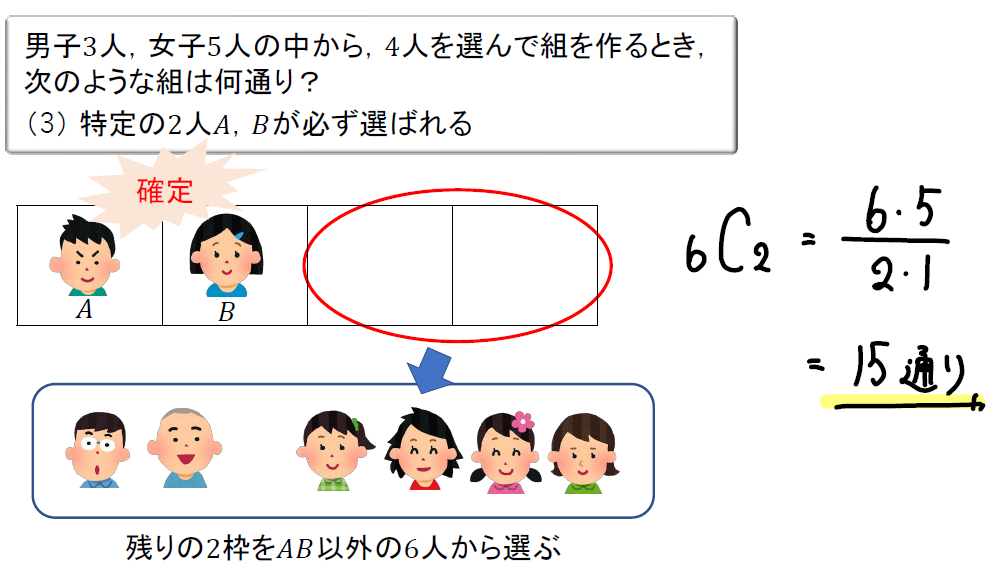
（3）特定の2人A、Bが必ず選ばれる

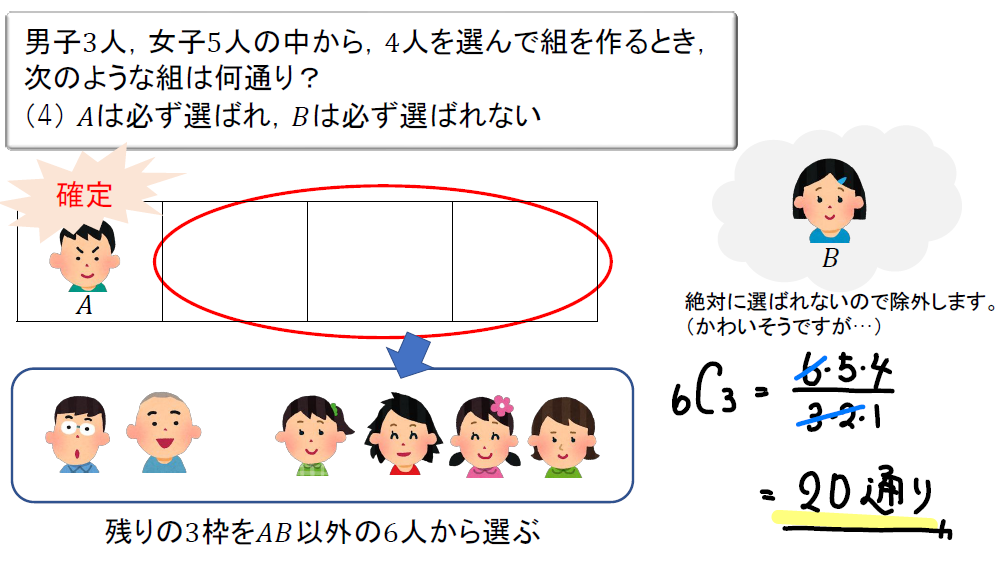
（4）Aは必ず選ばれ、Bは必ず選ばれない

解答・解説はこちら

答え

（1）30通り

（2）65通り

（3）15通り

（4）20通り

まとめ！

お疲れ様でした！

これで組み合わせCの計算方法についてはバッチリかな？

計算自体はそんなに難しいものではありませんでしたね。

だけど、PとCの使い分けが初めのうちは難しく感じるかもしれません。

最後のところで説明したように

選んで並べるなら順列P。

選んで終わりなら組み合わせC。

このように覚えておけば大丈夫！

あとは、たくさん練習して使いこなしが完璧になるように頑張っていきましょう。

ファイトだ(/・ω・)/

こちらの記事も合わせてどうぞ！

【苦手な人向け】組み合わせCの計算のやり方を簡単にサクッと解説するぞ！