今回は中1で学習する作図の単元から
三角形の高さを作図する問題について解説していくよ!
三角形の高さを作図する問題というのは
こんなやつだね。
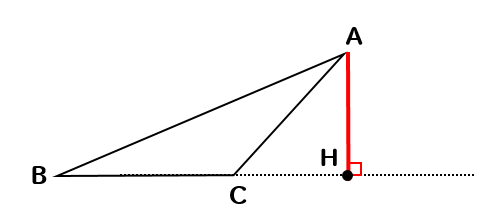
△ABCで、辺BCを底辺とし、高さAHとするときの点Hを作図しなさい。
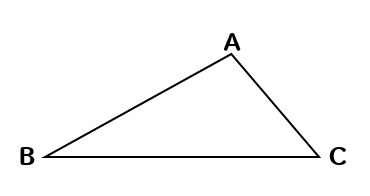
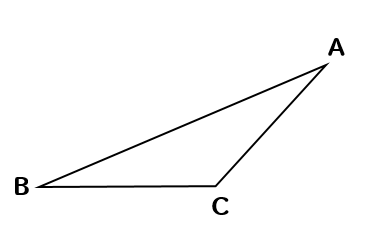
高さを作図する問題では
上のような2パターンの三角形があるので
それぞれの高さのかき方について解説していきます。
今回の記事は、こちらの動画でも解説しています(/・ω・)/
記事の最後には「基本作図の活用3選」ということで、模試、入試といった総合力を問われるテストに出てくるような演習課題も用意しています。
高さの作図について理解できた方は合わせて活用してみてください^^
三角形の高さの作図方法とは
三角形の高さを作図するには
頂点から底辺に対して垂直な線を引けばよいですね!
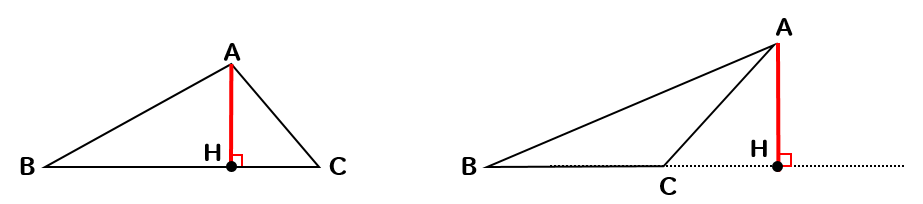
それでは
どのように垂直な線を引けばよいのか説明していきます。
まずは最初の三角形から見ていきましょう。

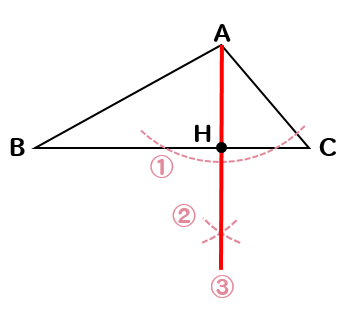
まずは、高さのてっぺんとなる頂点Aにコンパスの針を置いて
辺BCと交わるくらいの半径を持つ円を作図します。
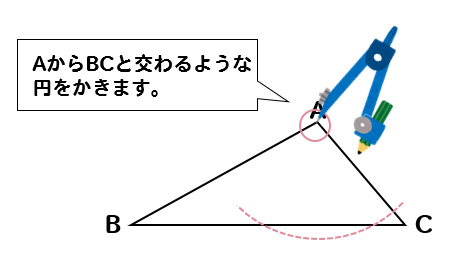
次に、先ほど作図した円と辺BCとの交点にコンパスの針を置いて
同じ半径を持つ円を2つ作図します。
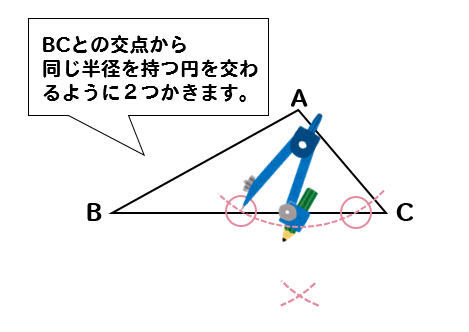
それぞれの円の交点が作図できたら
その交点と頂点Aを線で結んでやります。
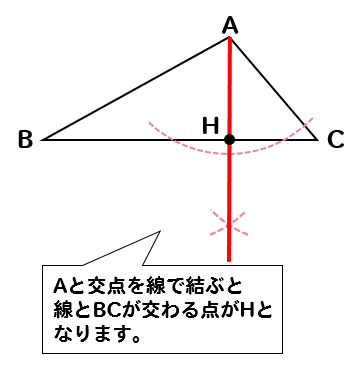
線を結んだときに、辺BCと交わる点が点Hとなります。
完成!!
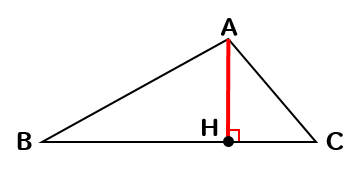
それでは、もう一つの三角形についても説明していきます。

こちらの三角形では、頂点Aから辺BCに垂直な線を引こうとすると
あれ…辺BCが足りない!?
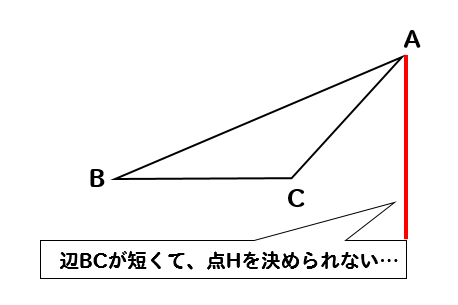
という状況になってしまいます。
そういう場合には事前に辺BCを延長してやりましょう。
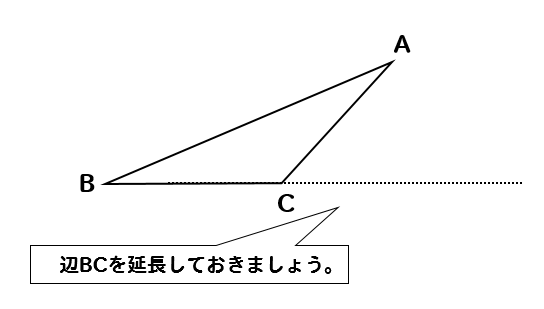
それでは、辺BCを延長できたところで
高さの作図を始めていきましょう。
ただ、ここからはさっきの三角形と全く同じになるので
少し割愛しながら説明していきます(^^;
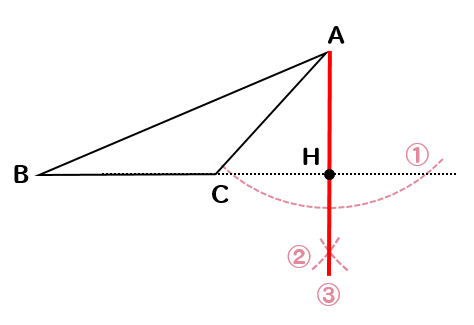
頂点Aにコンパスの針を置いて円を作図します。
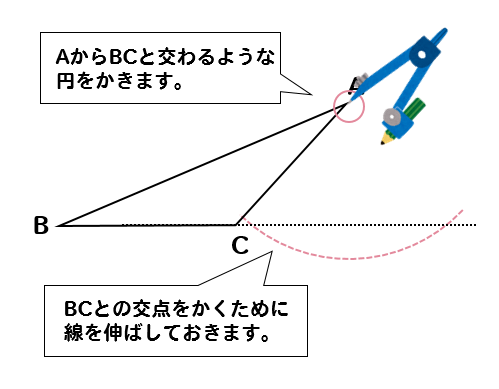
そうすると
先ほど延長しておいた線が活躍するはずです。
円と交わった部分にコンパスの針を置いて
同じ半径を持つ円をそれぞれ作図します。
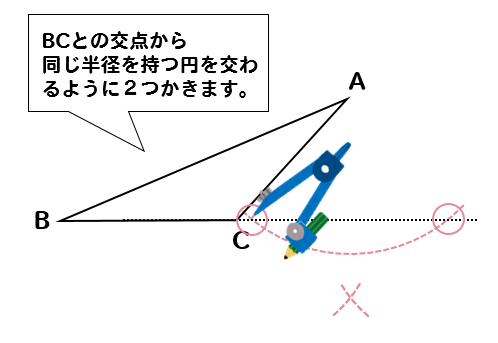
それぞれの円の交点が作図できたら
頂点Aと線を結んで、延長していた線と交わったところが点Hとなります。
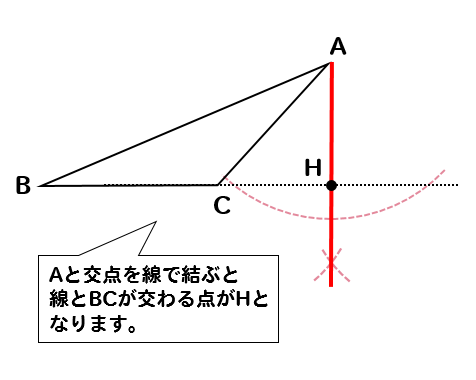
完成!!

テストはイジワル…!基本作図の活用3選
さて、ここまでのところで高さの作図について理解してもらえたと思います^^
ですが、
「よっしゃ、これでテストはバッチリだ!!」
と考えるのはちょっと早いんですね…(^^;)
というのも、テストになると「垂直二等分線」「角の二等分線」「垂線」
これら3つの基本作図を組み合わせた問題が出題されるようになるからです。
つまり、問題を読んだときに「どの作図を活用すればいいのか」「どの順番で作図していけばいいのか」といったことを瞬時に判断できるようにしておかないといけないんですね…
というわけで!
模試や入試によく出てくる基本作図を組み合わせた問題を用意しました(‘ω’)ノ
これを演習することで基本作図は100%の理解に到達できると思うので、テストを受ける前に必ず取り組んでおいてください!
□ たった3題で作図知識を入試レベルにアップさせる演習課題
□ 丸暗記ではない、問題文から導く作図の発想力を伝授!
□ 中1でも入試が解けちゃう!作図が武器になる基本活用術
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れます。
手を動かして作図を体験することで「テストでできる!」を実感することができますよ^^
こちらから今すぐチャレンジしてみよう!
三角形の高さ 作図のポイントまとめ
お疲れ様でした!
三角形の高さの作図はすごくシンプルなモノでしたね。
最後に確認のため作図のポイントをまとめておきましょう。
高さの作図ポイント
- 頂点Aから辺BCに交わるような円を作図する
- 辺BCと円との交点から、同じ半径の円を2つ作図する
- 2つの円の交点と頂点Aを線で結ぶと、辺BCとぶつかったところが頂点Hとなる
※ただし、垂直な線を引くために辺BCの長さが足りないときには事前に延長しておきましょう。
これで三角形の高さの作図はバッチリ(^^)!
高さをマスターしたら
次はいろんな角度を作図する問題にも挑戦してみましょう。
ファイトだー(/・ω・)/


















わかりやすかったです。すごく勉強になりました。ありがとうございました。
お役に立てて嬉しいです!
勉強がんばってくださいね!
とても分かりやすかったです!
嬉しいコメントありがとうございます!
とてもわかりやすかったです
勉強の参考になりました。
ありがとうございました。
嬉しいコメントありがとうございます!
勉強がんばってくださいね^^
ありがとうございました。とても分かりやすかったです。」
お役にてて良かったです!!
わかりやすかったです。ありがとうございました。(^^)
前回のテストでそれっぽく解き方を書いて、奇跡的に◯をもらったのですが、同じ問題が2回連続で出て、☓されました。
でも、このサイトではっきりとわかりました。本当にありがとうございます。
理解してもらえたようでよかったです