中学2年生で学習する「対頂角、同位角、錯角」についてサクッと解説しておきます。
それぞれの角の特徴をおさえて、角度を求める問題が解けるようにしておきましょう!
対頂角とは?
2つの直線が交わったときにできる角のうち
向かい合った角のことを対頂角(たいちょうかく)といいます。
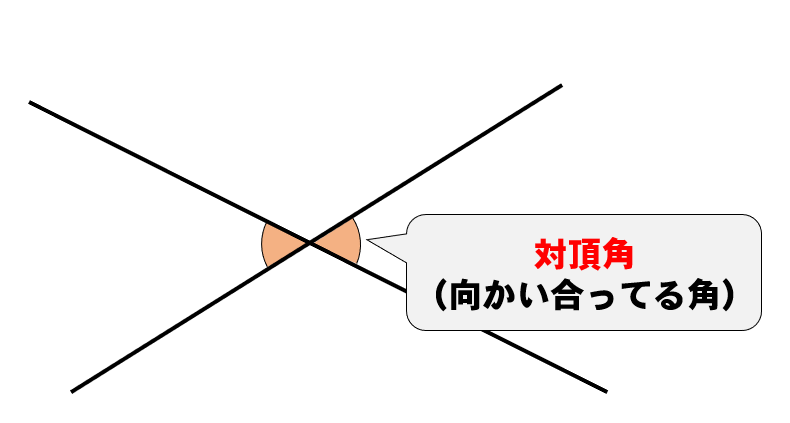
そして、すっごく大事なのが
対頂角は同じ大きさになるということです。
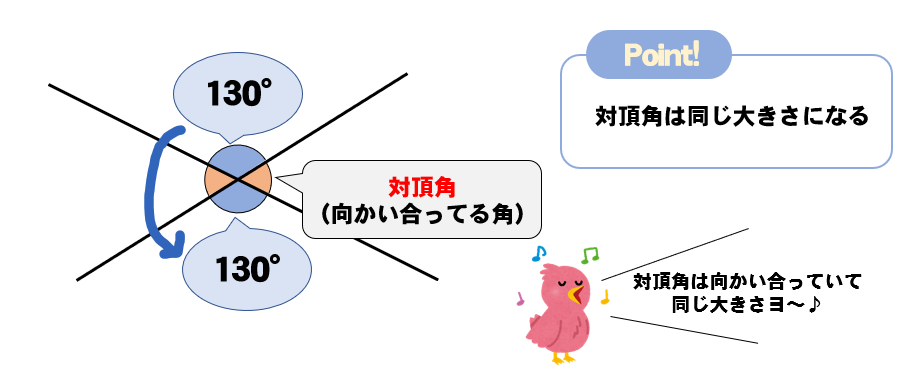
この性質は、のちに角度を求める問題を解く上で必須の知識となるので絶対に覚えておいてください。
また、対頂角についての注意も見ておきましょう。
対頂角は2本の直線が交わったときにできるものです。
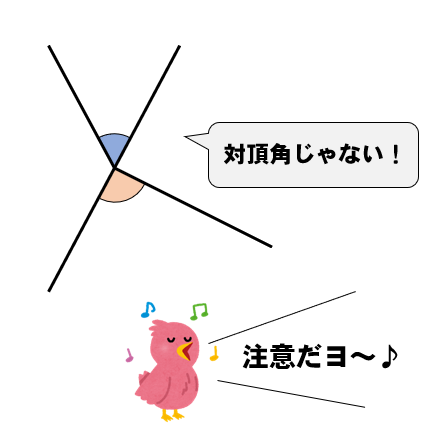
なので、このような場合には対頂角とは呼びません。
もちろん角の大きさも異なっているので注意が必要ですね。
対頂角が等しい理由
では、なぜ対頂角は同じ大きさになるのでしょうか。
理由は簡単なことです。
直線上は180°になるってことを使うと、\(∠a\)の隣の角は\(180-a\)と表すことができますね。
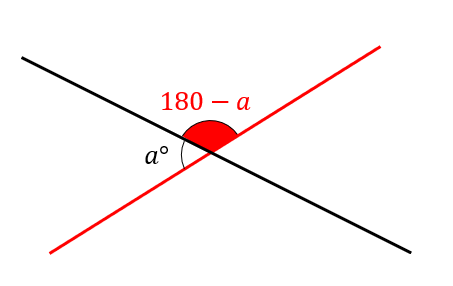
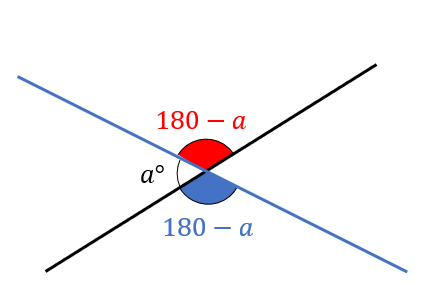
すると、向かい合っている角がともに\(180-a\)で表されたことになるので、大きさが等しくなるってことが確かめられました。
対頂角については、こちらの動画でも詳しく解説しています。
同位角、錯角とは
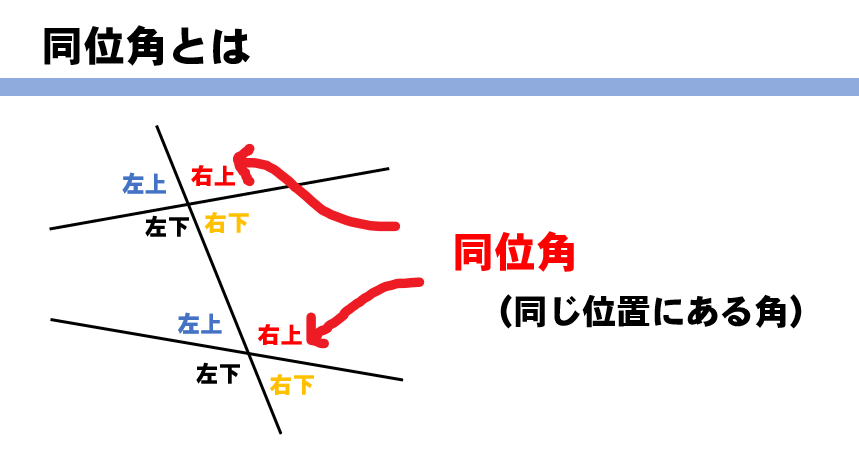
3本の直線が交わるとき、2か所に右上、右下、左上、左下と4つずつの角ができます。
このとき、右上どうし、左下どうしのように
同じ位置にある2つの角を同位角(どういかく)といいます。
同じ位置にある角
略して同位角と覚えておけば良いですね(^^)
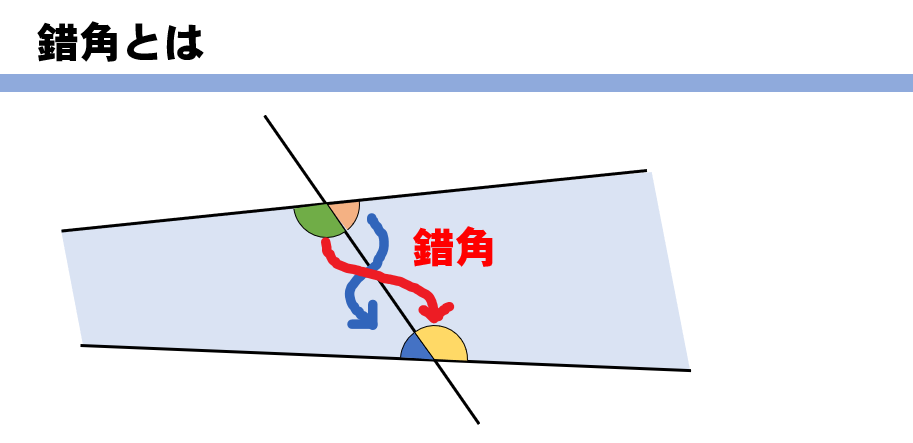
2本の直線の内側を見たときに、
それぞれが交差する位置にある2つの角を錯角(さっかく)といいます。
平行線と同位角、錯角

3本の直線の内、2直線が平行であるとき同位角、錯角はそれぞれ同じ大きさになります。
これは逆も言えて
同位角、錯角が同じ大きさであれば2直線が平行であるということもわかります。
平行線であれば、同位角、錯角は等しい。
これは問題を解いていく上で、すごく大切な性質になるので絶対に覚えておきましょう。
同位角、錯角についてはこちらの動画でも詳しく解説しています。

練習問題に挑戦!
次の図において\(∠x\)の大きさを求めなさい。
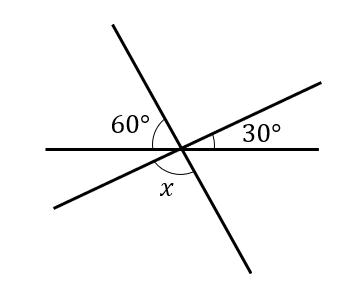
次の図において\(∠x\)の大きさを求めなさい。
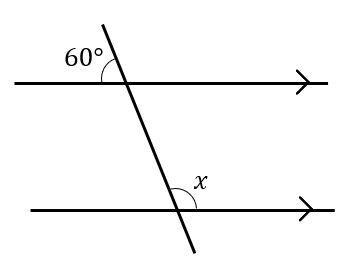
次の図において\(∠x\)の大きさを求めなさい。
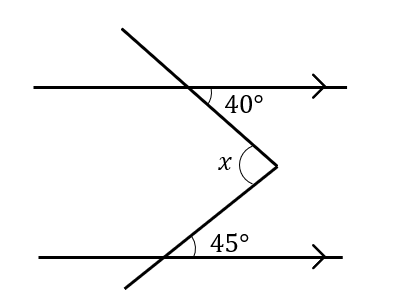
まとめ!
対頂角とは、2つの直線が交わったときの向かい合う角のこと。
角の大きさが等しくなります。
3本の直線が交わったときにできた8つの角のうち
同じ位置にある角を同位角
内側の角のうち、交差する位置にある角を錯角といいます。
2直線が平行になるときには、同位角、錯角は同じ大きさになります。
それぞれの特徴をしっかりと覚えて、すらすらと問題が解けるように練習しておきましょう(/・ω・)/



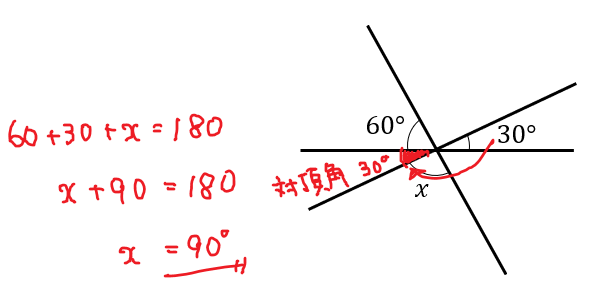
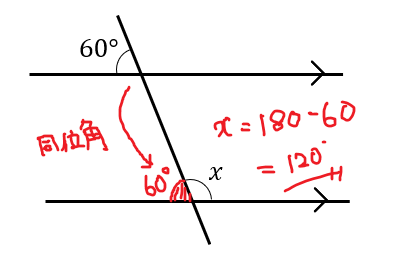















とても理解できた
めっちゃ分かりやすいっす。
一生このサイト見ます。☺️