今回は、中2で学習する証明問題の書き方について解説していきます。
証明問題って苦手な人が多いよね(^^;
だけど、しっかりとした手順を身につけてもらえれば、すっごく簡単に解くことができるようになるよ！
今回の記事では、三角形の合同を証明する問題を基礎からみっちりと解説していくね！
それでは、次の問題を利用して証明の書き方について解説していきます。
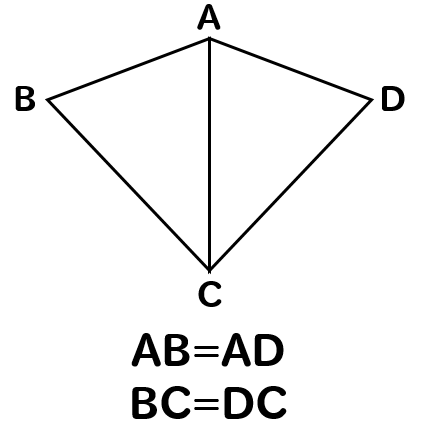
下の図で、AB=AD、BC=DCならば、△ABC≡△ADCとなることを証明しなさい。
Contents
証明の手順とは
証明問題が与えられたときには
いきなり証明を書こうとせずに
本当に△ABC≡△ADCとなるのか！？
ということを調べましょう。
今回の問題であれば
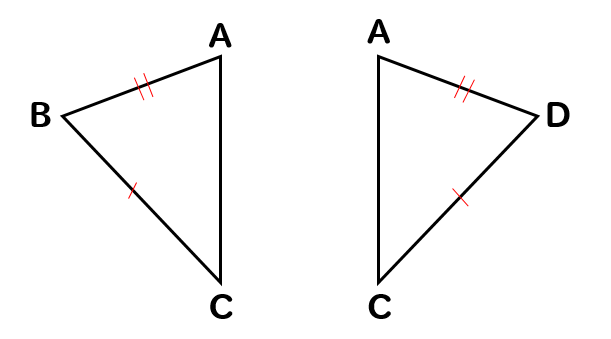
仮定から2辺が等しいことがわかっていますね。
そして
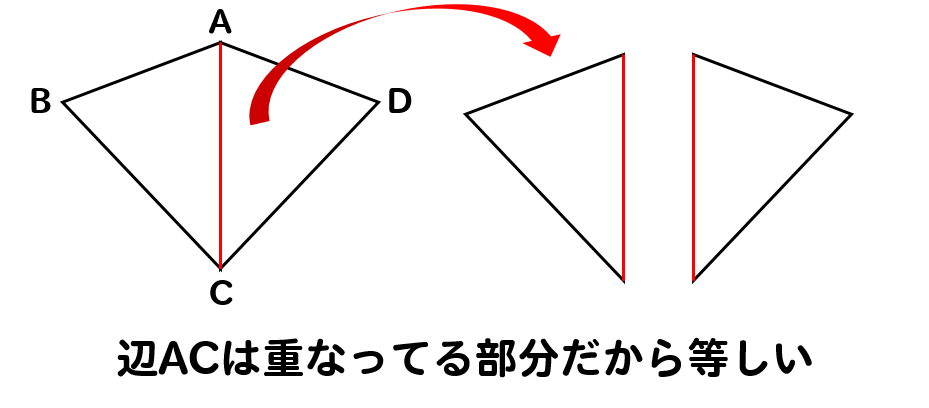
辺ACの部分は重なっているところだから、当然等しくなるよね。
こういう重なっている辺のことを
『共通な辺』と言いましたね。
忘れちゃった人は、こちらの記事で確認しておきましょう。
すると
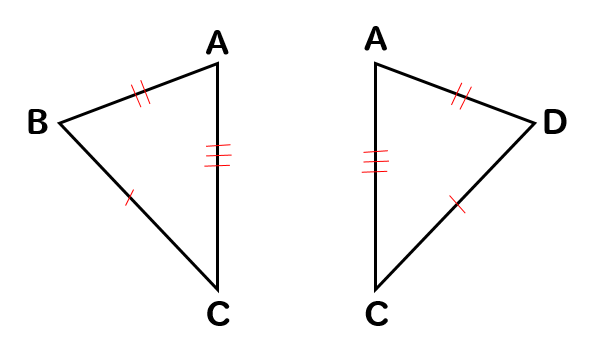2つの三角形は
3組の辺がそれぞれ等しいので
合同だということがわかりますね。
あ！
本当に△ABC≡△ADCになるわね
ということが確認出来たら
証明を書き始めていきます。
証明の書き方は以下の通りです。
証明の書き方 手順
- 注目する三角形を書く
- 仮定から分かることを書く
- 自分で見つけたことを理由付きで書く
- 合同条件からの結論
証明を書いてみよう！
それでは、上で紹介した手順通りに証明を書いてみましょう。
①注目する三角形を書く
今回は△ABCと△ADCに注目して証明を進めていくので
というように、注目する三角形を書いて
証明を開始していきます。
②仮定から分かることを書く
次に、仮定から分かることを書いていきます。
仮定から、AB=AD、BC=DCということが分かりましたね。
ということで
△ABCと△ADCにおいて
仮定より
AB=AD ・・・①
BC=DC ・・・②
というように書いてやります。
仮定から分かることだよ～ってことをちゃんと相手に伝えてあげるために
『仮定から』
っていうのも書いてあげましょう。
その方が相手も分かりやすくて、親切だもんね。
そして、たくさん情報が出てくるので整理しやすいように
・・・①
・・・②
のように、情報に番号をつけておきます。
③自分で見つけたことを理由付きで書く
次は、自分で見つけてきた情報を書きます。
今回は、このように問題には書いてないけど
共通な辺だからAC=ACになるということを自分で見つけてきました。
これを証明の中に書いていきます。
△ABCと△ADCにおいて
仮定より
AB=AD ・・・①
BC=DC ・・・②
共通な辺だから
AC=AC ・・・③
ここでポイントなのは
ちゃんと分かりやすい理由を書くことですね。
問題には書いていない情報なんだから
相手にちゃんと納得してもらえるように理由も明確に書きましょう。
今回であれば『共通な辺だから』というのが理由になりますね。
これを見れば
あ、辺が重なっているから等しいのか
ということが、しっかりと伝わります。
④合同条件からの結論
ここまでの情報をまとめると
3組の辺がそれぞれ等しいので
2つの三角形は合同だということがわかります。
△ABCと△ADCにおいて
仮定より
AB=AD ・・・①
BC=DC ・・・②
共通な辺だから
AC=AC ・・・③
①②③より
3組の辺がそれぞれ等しいので
△ABC≡△ADC
これで証明は完成となります。
しっかりと手順通り進めていければ
別に難しいような問題ではありませんね(^^)
ちょっと難しい部分があるとしたら
手順③ 自分で見つけてきたことをかく
という部分ですね。
証明が苦手な人は
ここで止まってしまう人が多いですね。
問題に書いていないことを
自分で見つけることができないと手順③をクリアすることができません。
なので、証明が苦手な人は
いろんな証明問題を見て
まずは、書く練習ではなく
見つける練習をするようにしてみてください。
さて、証明の手順がわかったところで
練習問題を通して、理解を深めていきましょう。
練習問題に挑戦！
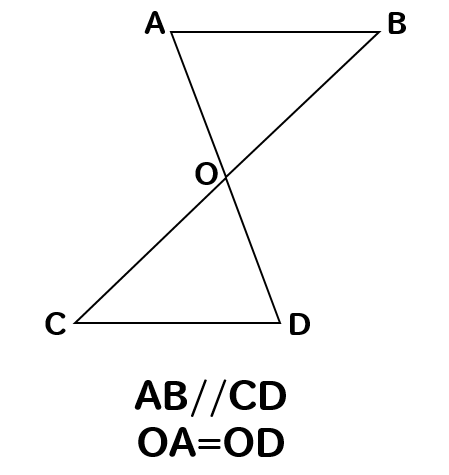
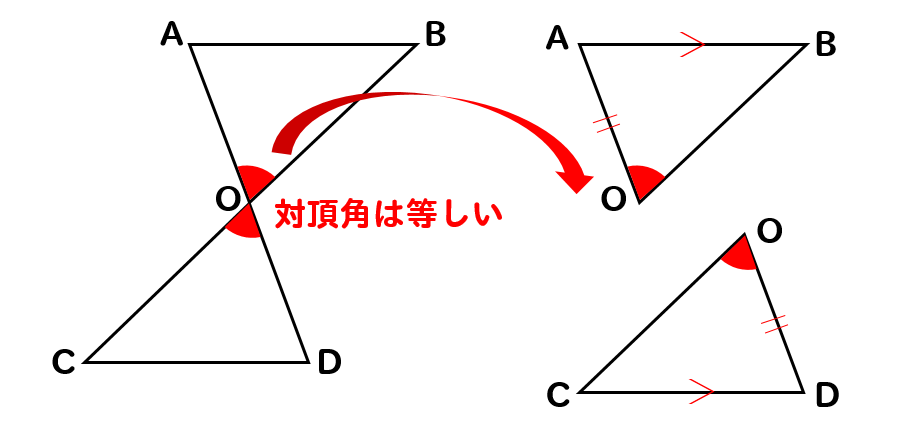
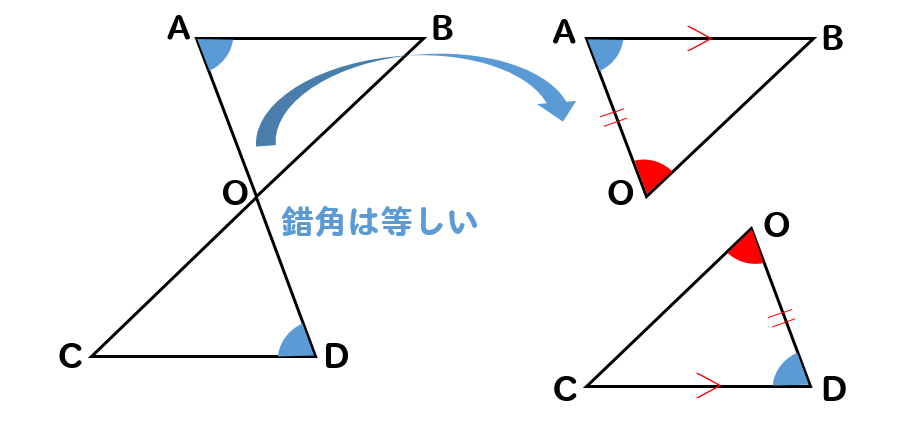
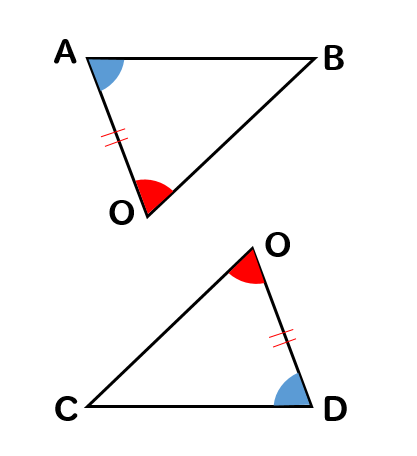
下の図で、AB//CD、OA＝ODならば△AOB≡△DOCとなることを証明しなさい。
仮定から分かること以外に
対頂角は等しくなるので
また、問題文にAB//CDとあるので
このように錯角が等しくなるから
ということが読み取れます。
それらをまとめると
1組の辺とその両端の角がそれぞれ等しくなるので
△AOB≡△DOCということがわかります。
それでは、これらのことをまとめて証明を書いていきましょう。
△AOBと△DOCにおいて
仮定より
OA＝OD ・・・①
対頂角は等しいので
∠AOB＝∠DOC ・・・②
AB//CDより、錯角は等しいので
∠BAO＝∠CDO ・・・③
①②③より
1組の辺とその両端の角がそれぞれ等しいので
△AOB≡△DOC
証明のかき方 基礎 まとめ
お疲れ様でした！
証明問題のポイントとしては
まず、証明を書き始める前に
結論が正しいかを確認していきましょう。
そして、正しいことの確認が取れたら
証明を以下の手順でかいていきます。
- 注目する三角形を書く
- 仮定から分かることを書く
- 自分で見つけたことを理由付きで書く
- 合同条件からの結論
手順が身についてくれば
あとは、ひたすら練習あるのみだ！
ファイトだー(/・ω・)/
【証明の書き方】合同な三角形の証明問題の書き方を基礎から解説！←今回の記事
【直角三角形】証明問題の書き方とは？合同条件の使い方を徹底解説！
効率よく学習を進めていきたい方は必見！
この記事を通して、学習していただいた方の中にはもっといろんな単元の学習を進めていきたい！
という素晴らしい学習意欲を持っておられる方もいる事でしょう。
だけど
どこの単元を学習すればよいのだろうか。
何を使って学習すればよいのだろうか。
勉強を頑張りたいけど 何をしたらよいか悩んでしまって
手が止まってしまう…
そんなお悩みをお持ちの方もおられるのではないでしょうか。
そんなあなたには
スタディサプリを使うことをおススメします。
スタディサプリを使うことで
どの単元を学習すればよいのか 何を解けばよいのか
そういった悩みを全て解決することができます。
スタディサプリでは学習レベルに合わせて授業を進めることが出来るほか、たくさんの問題演習も行えるようになっています。
スタディサプリが提供するカリキュラム通りに学習を進めていくことで
何をしたらよいのか分からない…
といったムダな悩みに時間を割くことなく
ひたすら学習に打ち込むことができるようになります(^^)
また、スタディサプリにはこのようなたくさんのメリットがあります。
- 費用が安い！月額1980円で全教科全講義が見放題です。
- 基礎から応用まで各レベルに合わせた講義が受けれる
- 教科書に対応！それぞれの教科に沿って学習を進めることができる
- いつでもどこでも受講できる。時間や場所を選ばず受講できます。
- プロ講師の授業はていねいで分かりやすい！
- 都道府県別の受験対策もバッチリ！
- 合わないと感じれば、すぐに解約できる。
今までの悩みを解決し、効率よく学習を進めていきましょう。
「最近、成績が上がってきてるけど塾でも通い始めたの？」
「どんなテキスト使ってるのか教えて！」
「勉強教えてーー！！」
スタディサプリを活用することで どんどん成績が上がり
友達から羨ましがられることでしょう(^^)
今まで通りの学習方法に不満のない方は、スタディサプリを使わなくても良いのですが
学習の成果を高めて、効率よく成績を上げていきたい方
是非、スタディサプリを活用してみてください。
スタディサプリでは、14日間の無料体験を受けることができます。
まずは無料体験受講をしてみましょう！
⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓
スタディサプリ小・中学講座
スタディサプリ高校講座
数スタの公式LINEを開設しました！