正多角形の1つの内角・外角を求める方法を問題解説！

今回は、正多角形の1つの内角・外角を求める方法について解説していくよ！

 

• そもそも正多角形ってなに？
• 1つの外角を求める方法は？
• 1つの内角を求める方法は？
• 問題に挑戦してみよう！

 

この4つのテーマでお話をしていきます(^^)

今回の記事内容は、こちらの動画でも解説しています(/・ω・)/

 

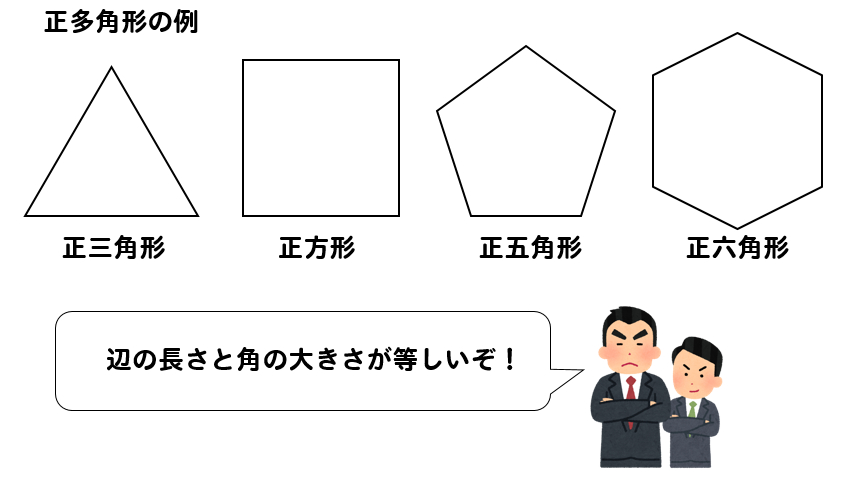
正多角形ってなに？どんな特徴があるの？

正多角形というのは

すべての辺の長さが等しくて

すべての内角の大きさが等しい多角形のことを言います。

 

 

そして

内角・外角を考えていくときには

正多角形は角がすべて等しい

 

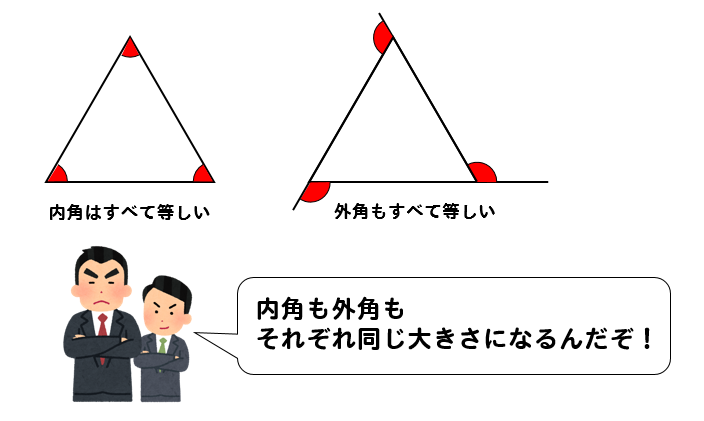
この性質を使って考えていくので、しっかりと頭に入れておきましょう！

 

１つの外角を求める方法

それでは、正多角形の１つの外角を求める方法についてですが

まず、外角の性質について知っておいて欲しいことがあります。

それは…

外角は何角形であろうと

全部合わせたら360°になる！

 

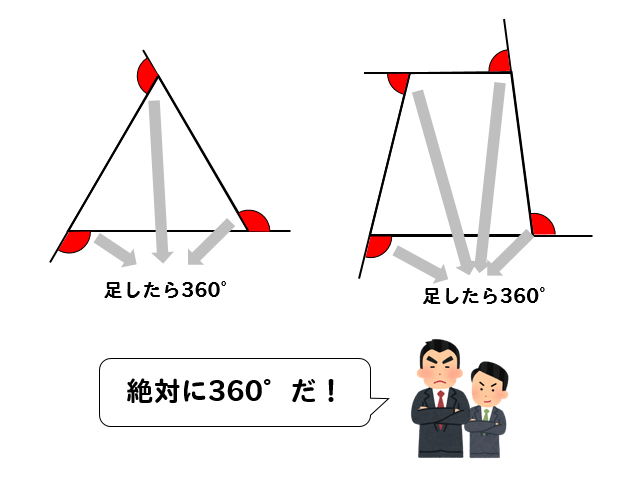
この性質は多角形、正多角形に関係なく

どんなやつでも全部合わせたら360°になります。

 

 

では、このことを使って考えると

正多角形の外角1つ分の大きさは

$$\LARGE{360 \div (角の数)}$$

をすることによって求めることができます。

 

正三角形の場合

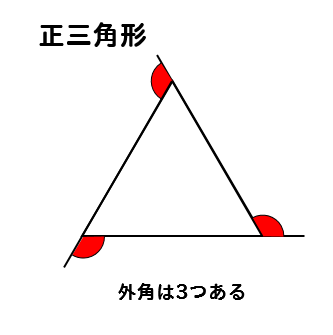
外角は3つあるので

360°を3つに分ければ1つ分の外角を求めることができると考えて

$$\LARGE{360 \div 3 =120°}$$

 

よって、正三角形の外角1つは\(120°\)ということがわかります。

正方形の場合

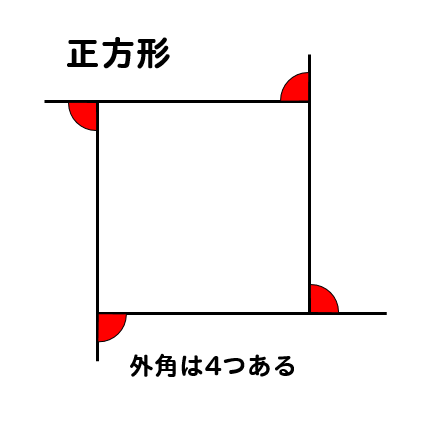
外角は4つあるので

360°を4つに分ければ1つ分の外角を求めることができると考えて

$$\LARGE{360 \div 4 =90°}$$

 

 

よって、正方形の外角1つは\(90°\)ということがわかります。

正五角形の場合

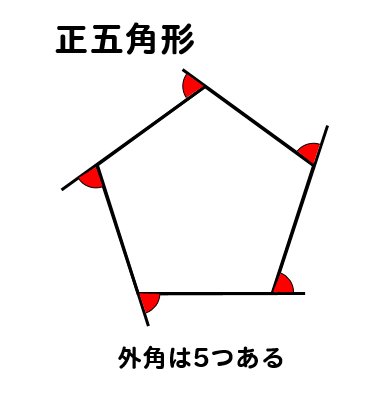
外角は5つあるので

360°を5つに分ければ1つ分の外角を求めることができると考えて

$$\LARGE{360 \div 5 =72°}$$

 

 

よって、正五角形の外角1つは\(72°\)ということがわかります。

 

 

ここまでやれば

大体のやり方は分かってもらえたでしょうか？？

とにかく、360°から角の数だけ割ってやれば1つ分を出すことができますね！

 

正六角形の外角は\(360 \div 6 =60°\)

正八角形の外角は\(360 \div 8=45°\)

正九角形の外角は\(360 \div 9=40°\)

正十角形の外角は\(360 \div 10=36°\)

正十二角形の外角は\(360 \div 12=30°\)

 

 

正七角形や正十一角形のように

$$360 \div 7=51.42…$$

$$360 \div 11=32.72…$$

割り切れないようなやつに関しては

おそらく問題として出てくることはないでしょうね。

 

１つの内角を求める2つの方法

それでは、次に内角を求める方法について考えていきましょう。

 

正多角形の内角1つ分を求めるには2つの方法があります。

• 外角を利用する方法
• 内角の和を考える方法

 

それぞれの方法について解説していきます。

外角を利用する方法

内角と外角って

必ず隣り合ってるよね！！

 

隣り合っているのだから

内角と外角を合わせると何度になるかわかる？

 

 

というわけで

内角と外角を足すと180°になるという特徴があります。

 

 

これを使って考えると

正多角形の内角1つ分の大きさは

$$\LARGE{180-(外角)}$$

このように求めてやることができます。

 

正三角形の場合

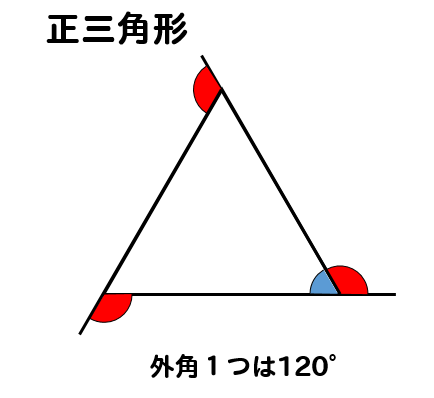
まず、外角1つ分の大きさを求めて

180°から外角1つ分の大きさを引いてやります。

 

先ほど外角の求め方のところで

120°になるということがわかっているので

 

正三角形の内角1つ分の大きさは

$$\LARGE{180-120=60°}$$

となります。

 

正五角形の場合

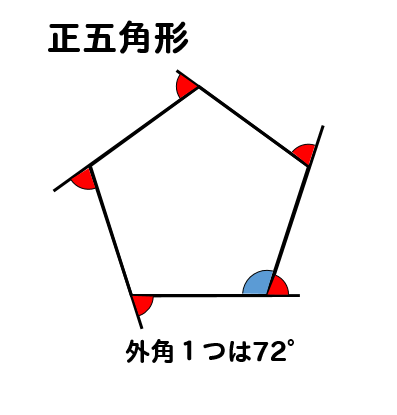
正五角形の1つ分の外角は72°となるので

内角1つ分の大きさは

$$\LARGE{180-72=108°}$$

となります。

 

 

同様に

正六角形の1つ分の内角は\(180-60=120°\)

正八角形の1つ分の内角は\(180-45=135°\)

正九角形の1つ分の内角は\(180-40=140°\)

正十角形の1つ分の内角は\(180-36=144°\)

正十二角形の1つ分の内角は\(180-30=150°\)

 

と求めてやることができます。

内角の和を考える方法

次は内角の和から1つ分の大きさを求める方法です。

まず、多角形の内角の和は

$$\LARGE{180 \times (n-2)}$$

で求めることができましたね。

 

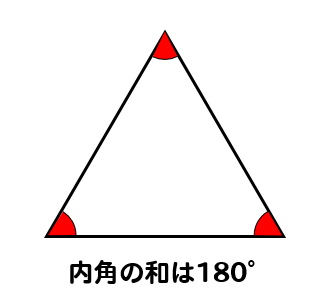
正三角形の内角の和であれば

$$\LARGE{180 \times (3-2)=180°}$$

 

正五角形の内角の和であれば

$$\LARGE{180 \times (5-2)=540°}$$

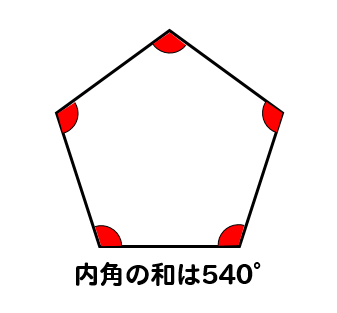
と求めてやることができます。

 

 

内角の和が求まれば

1つ分の大きさを求めることは簡単です。

外角のときと同じように割ってやればいいですね。

 

正三角形なら

$$\LARGE{180 \div 3 = 60°}$$

 

正五角形なら

$$\LARGE{540 \div 5 =108°}$$

となります。

 

 

 

外角を利用した考え方の方が

計算量が少ないのでおススメではありますが

両方のやり方をしっかりとマスターしておくと

応用力が高まってGOODですね。

 

 

それでは、内角・外角の求め方を

マスターしてもらったところで

問題演習に挑戦して理解を深めていきましょう！

 

問題に挑戦してみよう！

 

 

 

 

正多角形の内角・外角　まとめ

お疲れ様でした！

 

外角の和は常に360°になる

という性質は非常に便利でしたね。

 

問題でも大活躍する性質なので

絶対に覚えておきましょう。

 

内角が問題に出てきた場合でも

$$\LARGE{(内角)+(外角)=180°}$$

の性質を使っていけば、外角を利用しながら解くことができます。

 

 

さぁ

問題の解き方がわかったら

あとはひたすら演習あるのみ！

学校のワークや問題集を使って演習しまくろう

ファイトだー(/・ω・)/