二等辺三角形の定義と性質をサクッと確認しておこう！

二等辺三角形の「定義」「性質」についてサクッと確認しておきましょう。

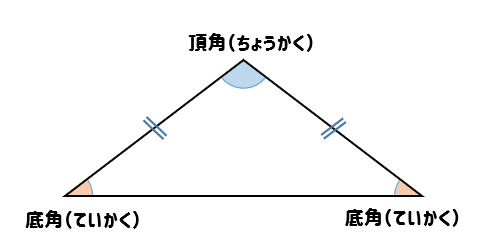
二等辺三角形の定義

⇒　2つの辺が等しい三角形。

二等辺三角形の性質（定理）

1. 2つの底角が等しい。
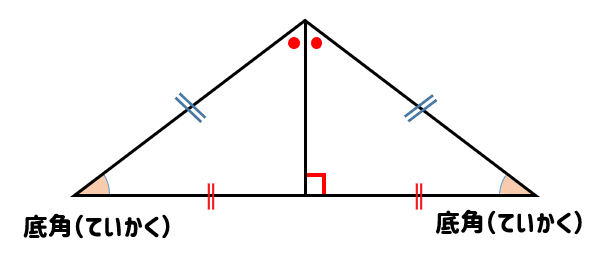
2. 頂角の二等分線は、底辺を垂直に二等分する。

定義？性質？なにが違うの？？

では、次の章で二等辺三角形の定義、性質について詳しく確認してみましょう。

二等辺三角形の定義と性質

定義とは、言葉の意味をはっきりと説明したモノのことです。

つまり、二等辺三角形ってなに？？

と聞かれたときに答える説明のことを定義といいます。

一方で、性質（定理）とは

定義をもとに証明されることの中で重要なモノのことをいいます。

二等辺三角形の定理とは

1. 2つの底角が等しい。
2. 頂角の二等分線は、底辺を垂直に二等分する。

この2つが挙げられるのですが、

これらは「2つの辺が等しい」という定義を用いて次のように証明されます。

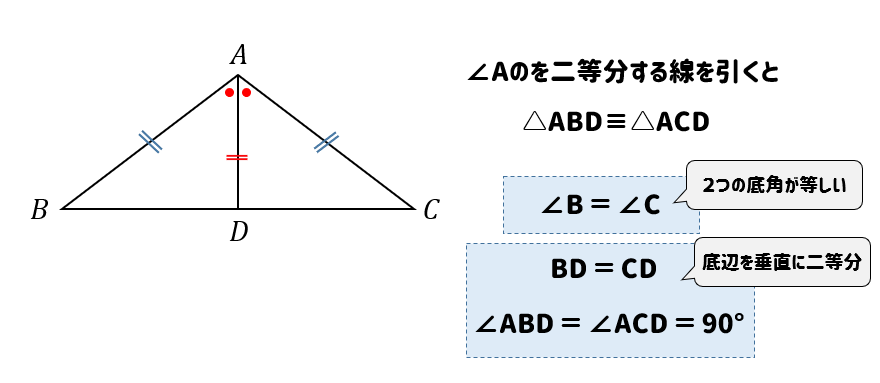
頂角を二等分する線を引くと、ADが共通な辺なので

2組の辺とその間の角が等しいことから

△ABDと△ACDが合同な図形であることがわかります。

合同な図形の対応する辺の長さ、角の大きさは等しくなるので

\(∠B=∠C\)、\(BD=CD\)、\(∠ABD=∠ACD=90°\)

ということが証明されます。

このように、定義を元に証明される特徴のことを性質（定理）といいます。

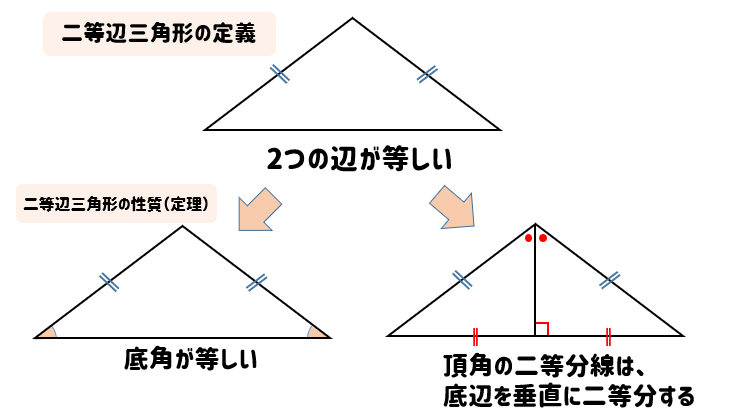
というわけで、二等辺三角形においては次の定義と性質（定理）をしっかりと覚えておきましょう。

二等辺三角形の性質を利用した問題

「底角が等しいという性質」はいろいろな問題で活用されます。

一番使われるのが、角を求める問題です。

∠\(x\)の大きさを求めなさい。

こちらの問題のように、二等辺三角形の角の大きさを求める場合

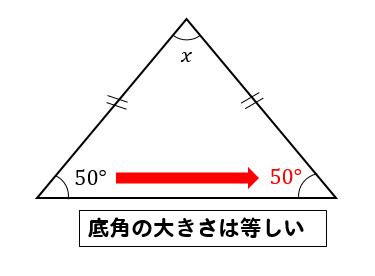
底角の大きさが等しくなることを使って求めるようになります。

$$x=180-(50+50)=80°\cdots(解)$$

二等辺三角形の角についての問題は、こちらの記事でまとめているのでご参考ください。

⇒ 二等辺三角形の角度の求め方を問題を使って徹底解説！

また、底角が等しいという性質は証明でも活用されます。

証明の中で二等辺三角形を見つけたら、

底角が等しいこと利用しながら合同条件を探していきます。

「頂角を二等分する線は、底辺を垂直に二等分する」という性質は、2年生のうちではあまり活用しません。

ですが、3年生で学習する「三平方の定理」という単元でバリバリに活躍していくことになるので、こちらも忘れずに覚えておきたい性質ですね。

こちらの性質を利用した問題はこちら。（中3生向け）

⇒ 高さがわからない二等辺三角形の面積の求め方！三平方の定理を使えばバッチリ！

まとめ！

以上、今回は二等辺三角形の定義と性質についてまとめておきました。

言葉を覚えるのは苦手…という方もいるかもしれませんが

図形と一緒にイメージで覚えてしまうのがいいですね。

二等辺三角形の定義、性質はすごく重要なものなので、

忘れずに覚えておきましょうね(/・ω・)/