今回は中2で学習する
特別な平行四辺形の単元の中から
面積が等しくなる三角形を見つける問題を解説していきます。
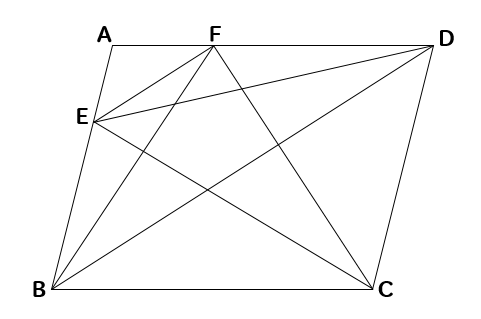
問題
下の図で、四角形ABCDは平行四辺形であり、EF//BDである。このとき、△CDFと面積の等しい三角形をすべて答えなさい。
今回の内容はこちらの動画内でも解説しています!
サクッと理解したい方は動画がおススメです^^
面積の等しい三角形を見つけるポイント!
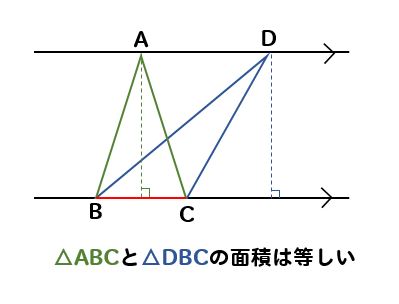
このように平行な線に挟まれている三角形は
底辺の長さが等しければ面積が等しくなります。
三角形の面積は
$$(底辺)\times(高さ)\times \frac{1}{2}$$
と求めることができますよね。
だから、底辺と高さが等しくなる三角形は
たとえ、形がこーんなに違っても
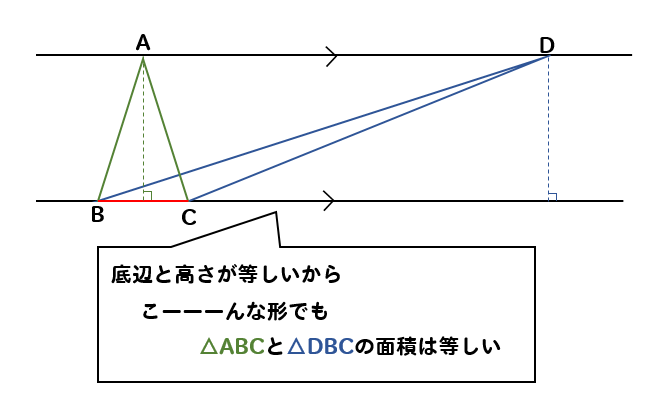
面積は等しくなります。
あ、平行線はどこをとっても距離が等しくなるっていう特徴も覚えておいてね!
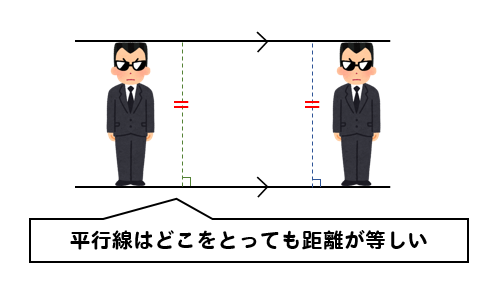
だから、どの三角形も高さは等しくなります。
問題の解説&答え
それでは、上で説明した特徴を活かして
平行な線に注目しながら
面積の等しい三角形を見つけていきましょう!
まず、四角形ABCDは平行四辺形なので
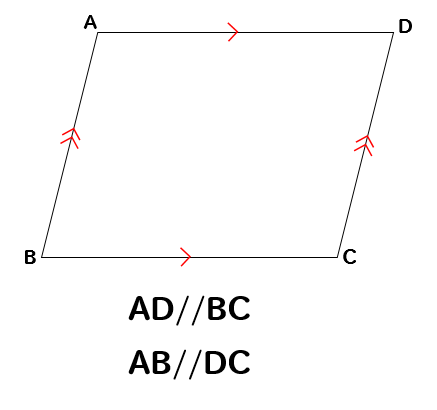
それぞれの向かい合う辺が平行になるということがわかります。
そして、このAD//BCを利用して
FDを底辺とする三角形に注目すると
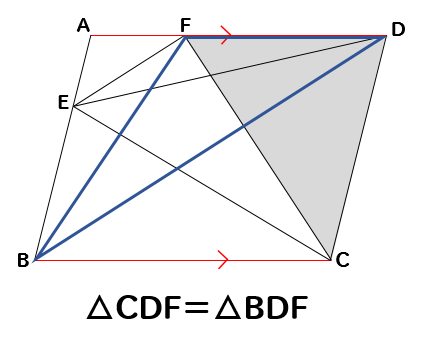
△CDF=△BDF
がわかります。
次は、先ほど見つけた△BDFと面積が等しくなる三角形を探します。
EF//BDを利用して、底辺をBDとする三角形に注目すると
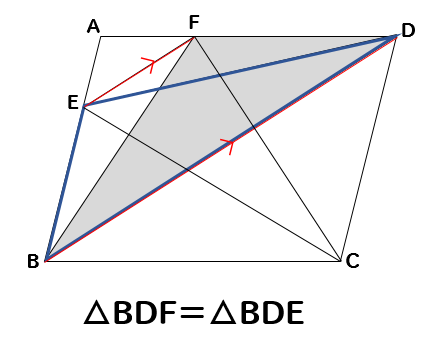
△BDF=△BDE
がわかります。
次も同様に、△BDEと面積が等しくなる三角形を探します。
AB//DCを利用して、底辺をEBとする三角形に注目すると
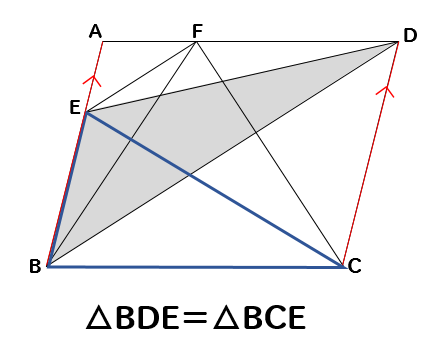
△BDE=△BCE
とわかります。
あれあれ…
問題では、△CDFと面積の等しくなる三角形を求めろと言っているのに
後半は△CDFと関係なくなっっちゃってんじゃん!

と思わないでください。
一連の流れで分かった情報をまとめていきます。
△CDF=△BDF
△BDF=△BDE
△BDE=△BCE
これらをまとめて表すと
△CDF=△BDF=△BDE=△BCE
となるわけですね。
よって、これらの三角形は全部面積が等しい!ということになります。
△CDF⇒△BDF⇒△BDE⇒△BCE
というようにリレー形式で
面積の等しくなる三角形を見つけていく感じですね!
答え
△BDF、△BDE、△BCE
だいたいのイメージが掴めた人は練習問題で理解を深めていきましょう。

練習問題に挑戦!
問題
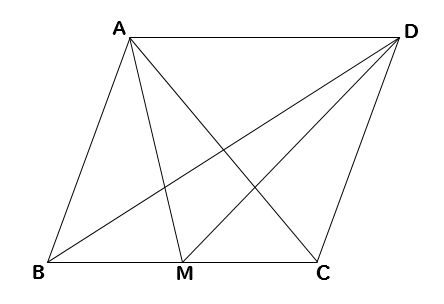
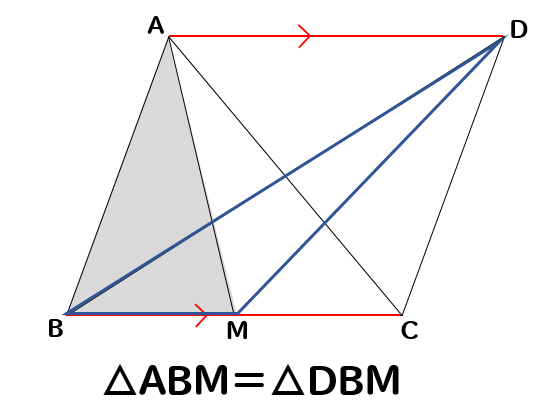
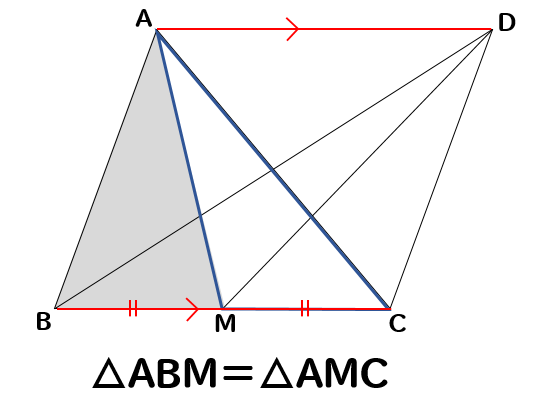
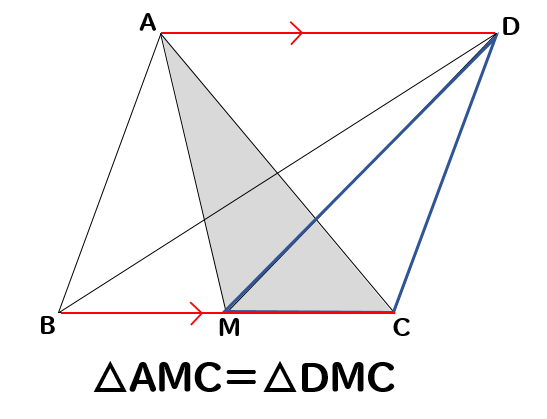
下の図で、四角形ABCDは平行四辺形である。点Mは辺BCの中点のとき、△ABMと面積の等しい三角形をすべて答えなさい。
まとめ
お疲れ様でした!
平行四辺形の中から面積の等しい三角形を見つけれるようになりましたか?
正直、慣れるまではなかなか難しい問題です。
平行四辺形に線がたくさんあって
どこを見ていけばいいのか分かりにくいもんね。
だけど、何度も練習していると
自然と面積の等しい三角形が浮き出て見えてくるようになります。
ポイントは
平行な線を見つけることですね。
そして、その平行な線に挟まれている三角形を探していくことです。
等しい三角形を見つけたら
そこからリレーをしていきながら、どんどんと三角形を見つけていってください。
ファイトだー(/・ω・)/
【証明の書き方】合同な三角形の証明問題の書き方を基礎から解説!
【直角三角形】証明問題の書き方とは?合同条件の使い方を徹底解説!















これのお陰で全く理解できなかったのが完璧に理解できました!ありがとうございました♪( ´▽`)
お役に立ててよかったです^^
引き続き数スタをよろしくお願いします(‘◇’)ゞ
先生の解説を聞いても理解できなかったのにこれのお陰でとてもよくわかりました!これで明日のテストも大丈夫だと思います!!