今回は中2数学で学習する図形と証明の単元から「平行四辺形になるための5つの条件」についてイチから解説していきます。
ここでは、ちょっとがんばって覚えてもらうことがあるので、気合を入れてがんばっていきましょう(‘ω’)ノ
今回のポイントはこちら!
そして、こちらの問題を解けるようになってもらいます!
【問題】
四角形ABCDで、対角線の交点をOとする。次の条件のうち、四角形ABCDがいつでも平行四辺形になるものを選びなさい。
(1)\(AB//DC, AD//BC\)
(2)\(AB//DC, AB=DC\)
(3)\(AB=BC, AD=DC\)
(4)\(OA=OC, OB=OD\)
(5)\(∠A=∠B, ∠C=∠D\)
では、それぞれ解説していきますね^^
解説動画はこちらです(‘◇’)ゞ
ちなみに、平行四辺形になるための証明にチャレンジしたい方はこちらの記事をどうぞ!
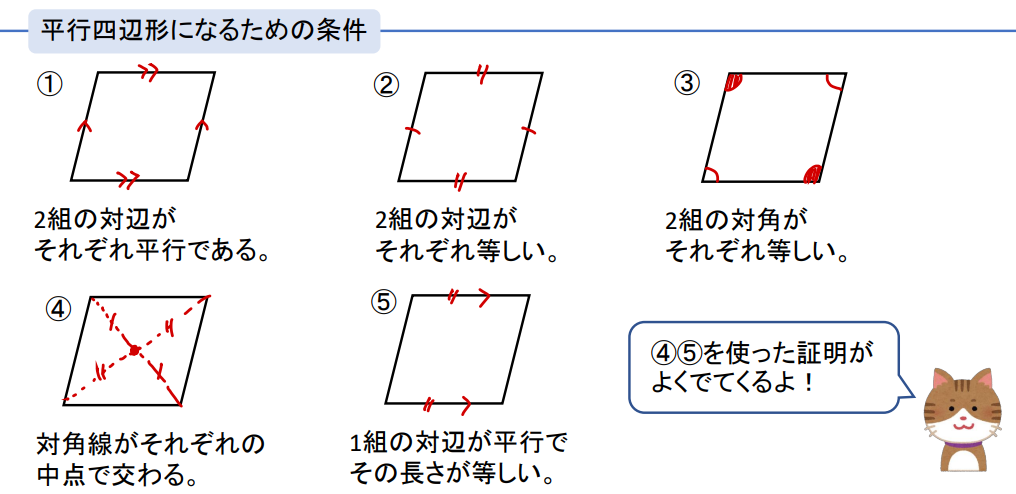
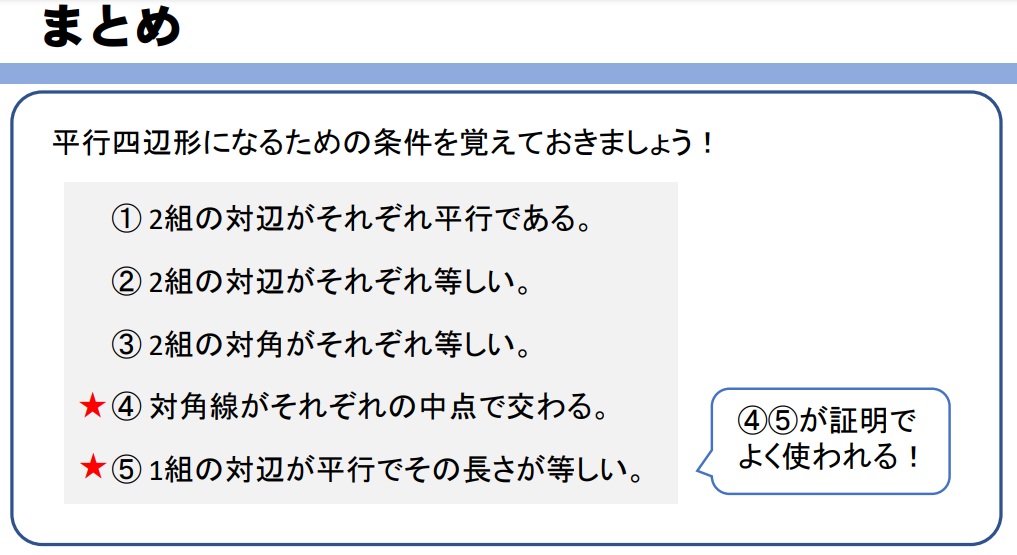
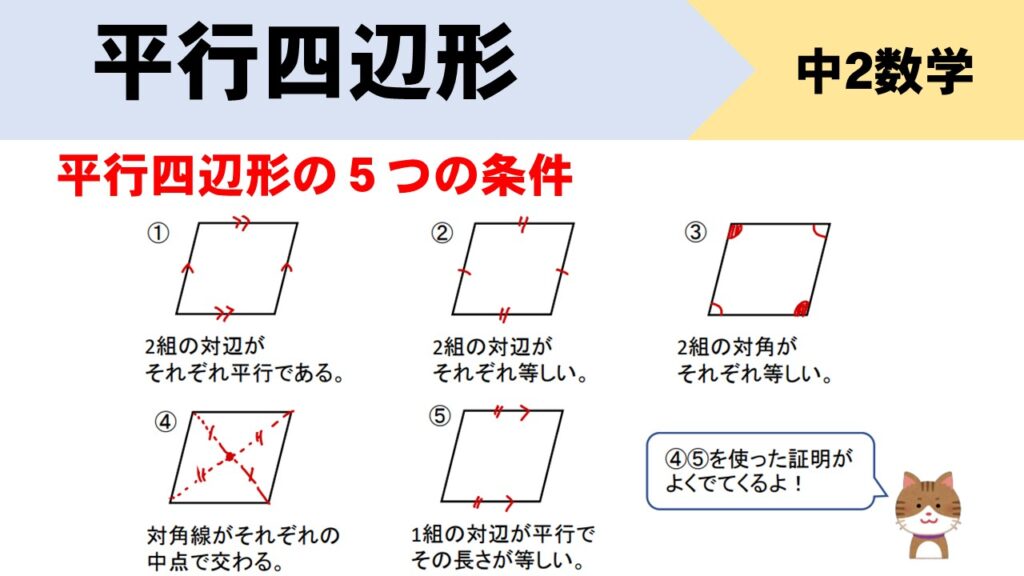
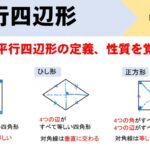
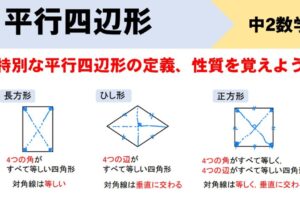
平行四辺形になるための5つの条件
四角形は、次の5つのどれかが成り立てば平行四辺形になります。

これを平行四辺形になるための5つの条件といいます。
ネコくんが喋っているように、④⑤の条件は証明でよく使われるため、他よりも重要度が高いことも頭に入れておいてください。
さぁ!こればっかりは考えていても仕方がありません。
声に出したり、紙に書き出すなりして暗記しましょう!
覚えれたぞ!と思った方はこちらの確認テストにチャレンジしてください(‘◇’)ゞ
【確認テスト】
次の図に当てはまる平行四辺形になるための条件を答えなさい。
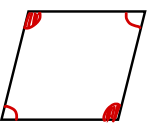
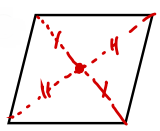
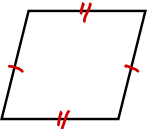
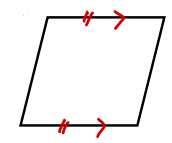
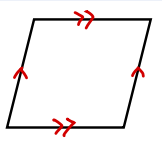
テストがバッチリだった人は次の問題に進みましょう!
どれが平行四辺形になる?
【問題】
四角形ABCDで、対角線の交点をOとする。次の条件のうち、四角形ABCDがいつでも平行四辺形になるものを選びなさい。
(1)\(AB//DC, AD//BC\)
(2)\(AB//DC, AB=DC\)
(3)\(AB=BC, AD=DC\)
(4)\(OA=OC, OB=OD\)
(5)\(∠A=∠B, ∠C=∠D\)
では、こちらの問題にチャレンジしてみましょう。
それぞれの条件を見ながら、平行四辺形になるための条件に当てはまるかをチェックします。
とはいえ…式を見ただけでは分かりにくいので、イメージ図を書きながら考えていきます。
(1)からイメージ図を使いながら確認してみましょう。
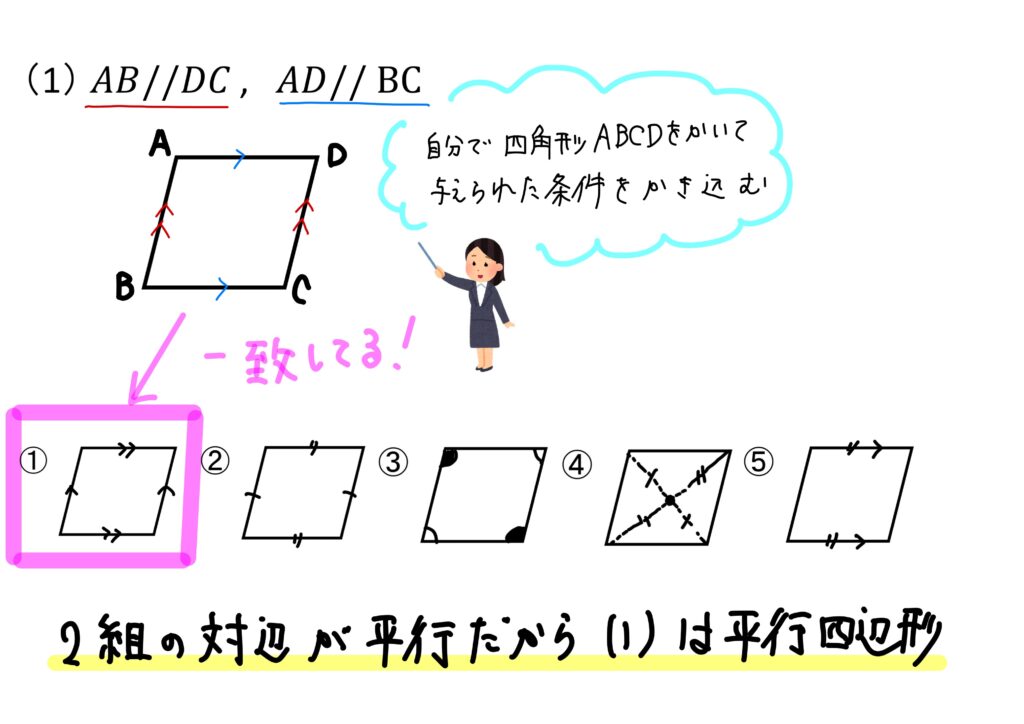
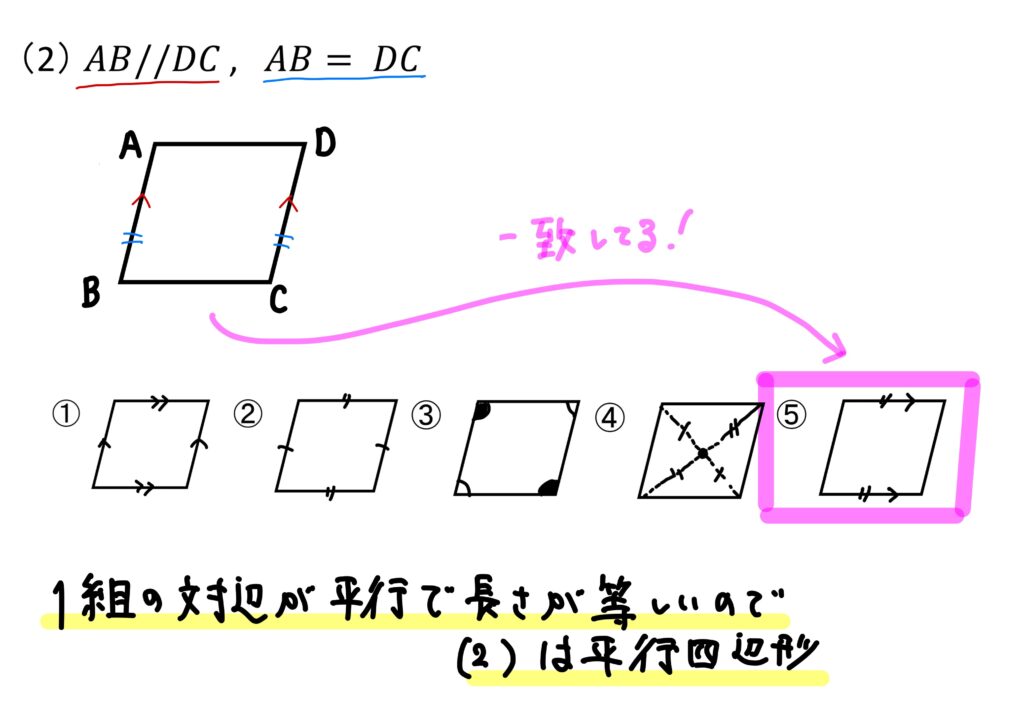
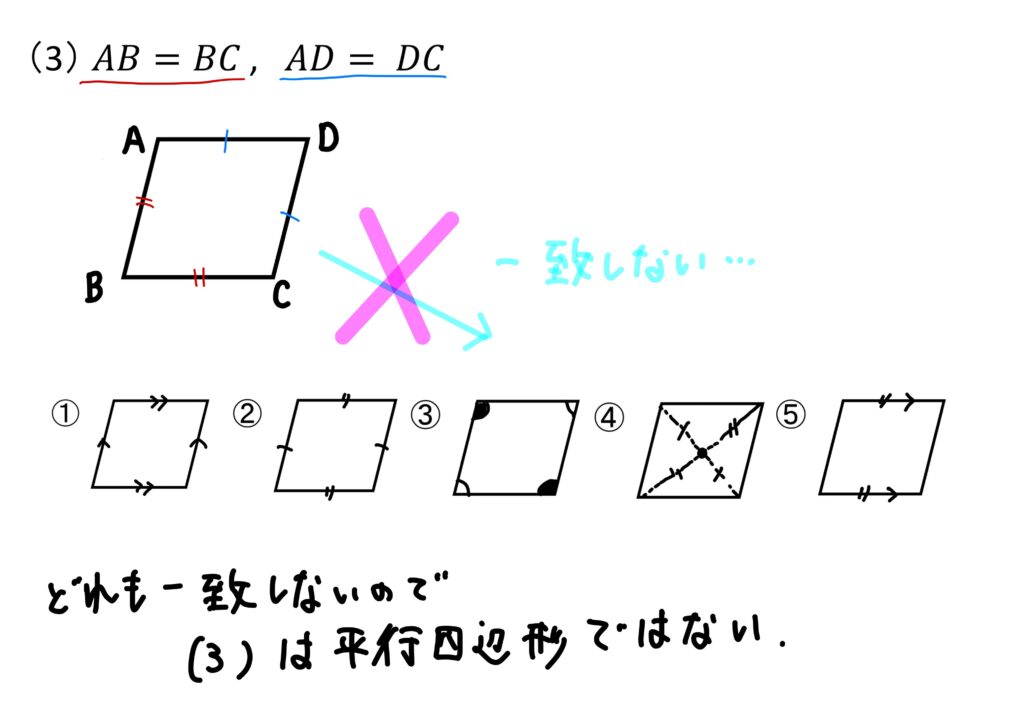
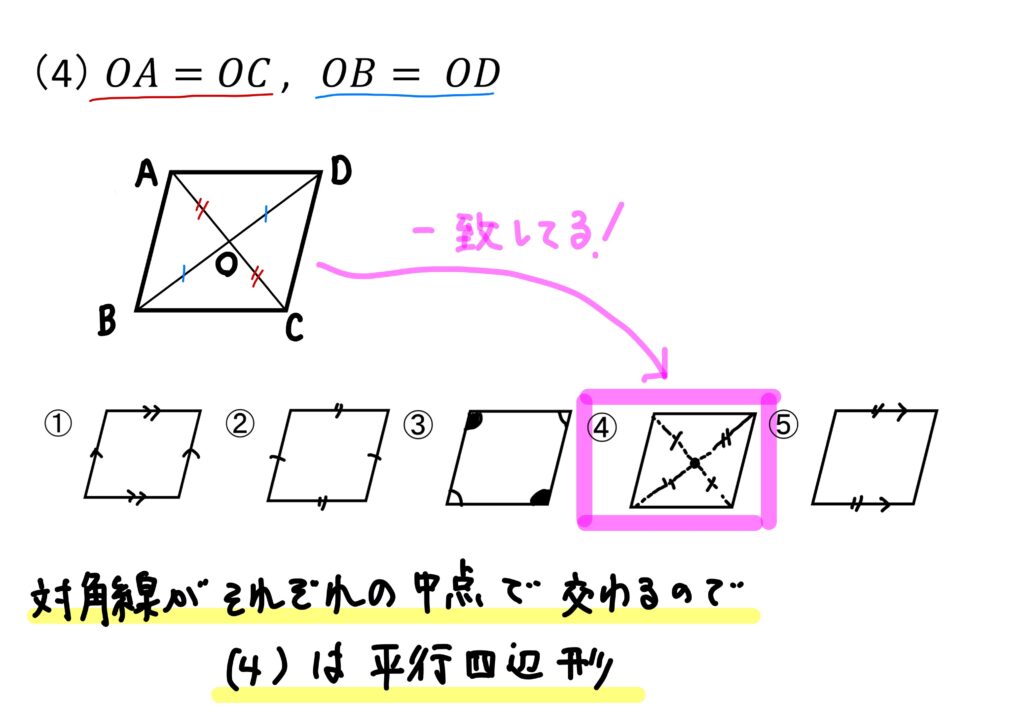
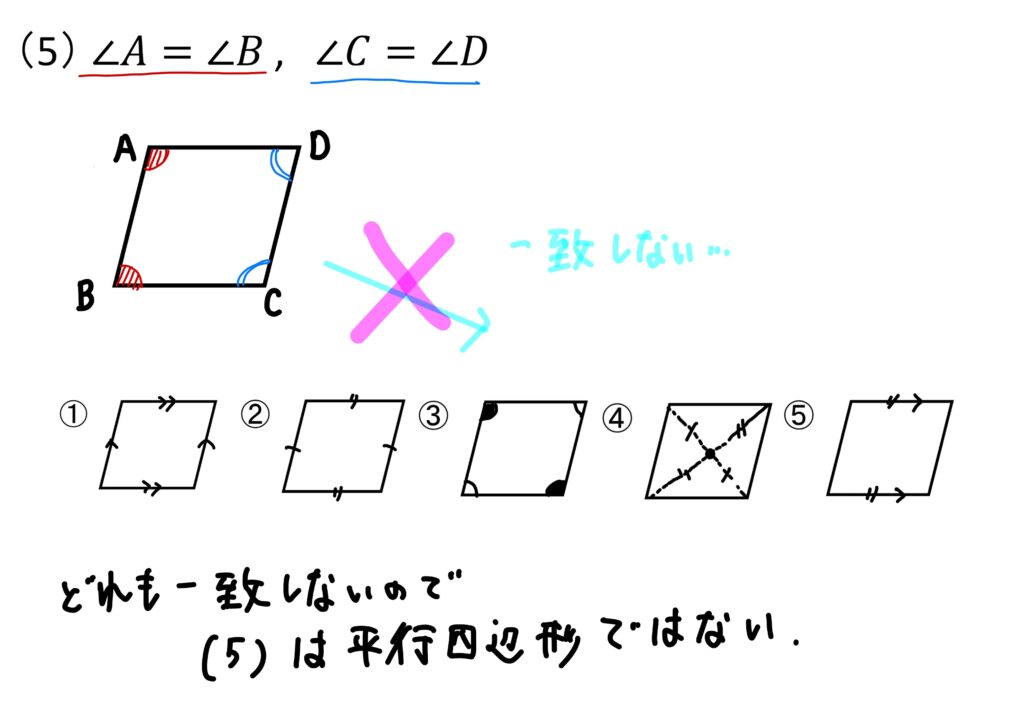
というわけで、平行四辺形になるのは(1)(2)(4)の3つですね!
答え
$$(1)(2)(4)$$
では、理解度を深めるために次の演習にチャレンジしてみましょう。
練習問題にチャレンジ!
【問題】
四角形ABCDで、対角線の交点をOとする。次の条件のうち、四角形ABCDがいつでも平行四辺形になるものを選びなさい。
(1)\(AB//DC, AB=DC\)
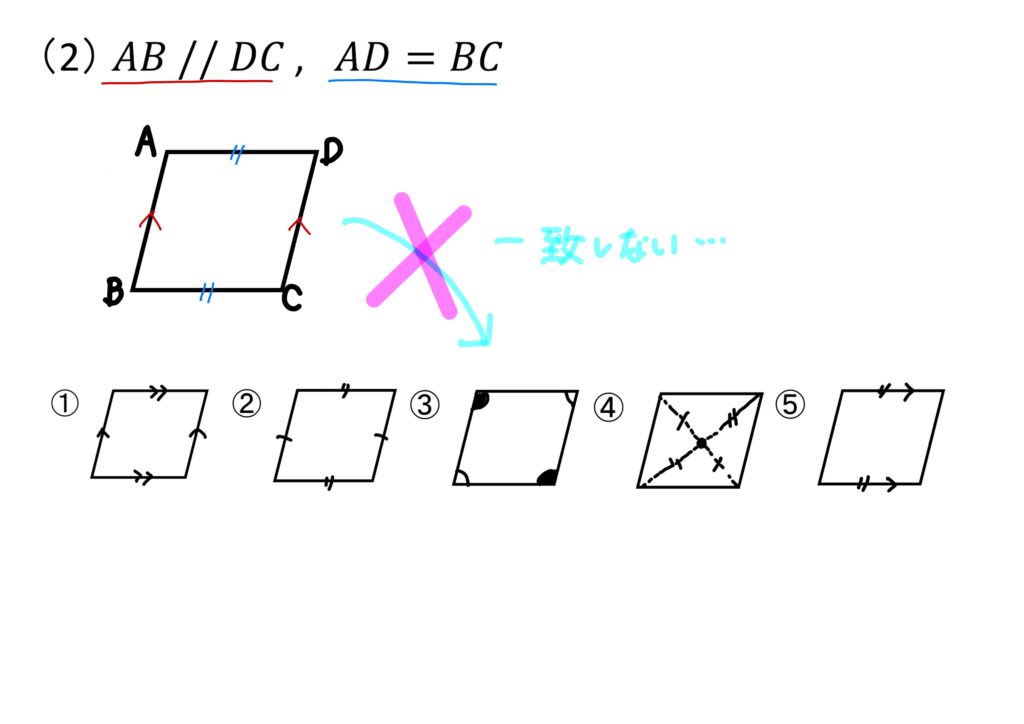
(2)\(AB//DC, AD=BC\)
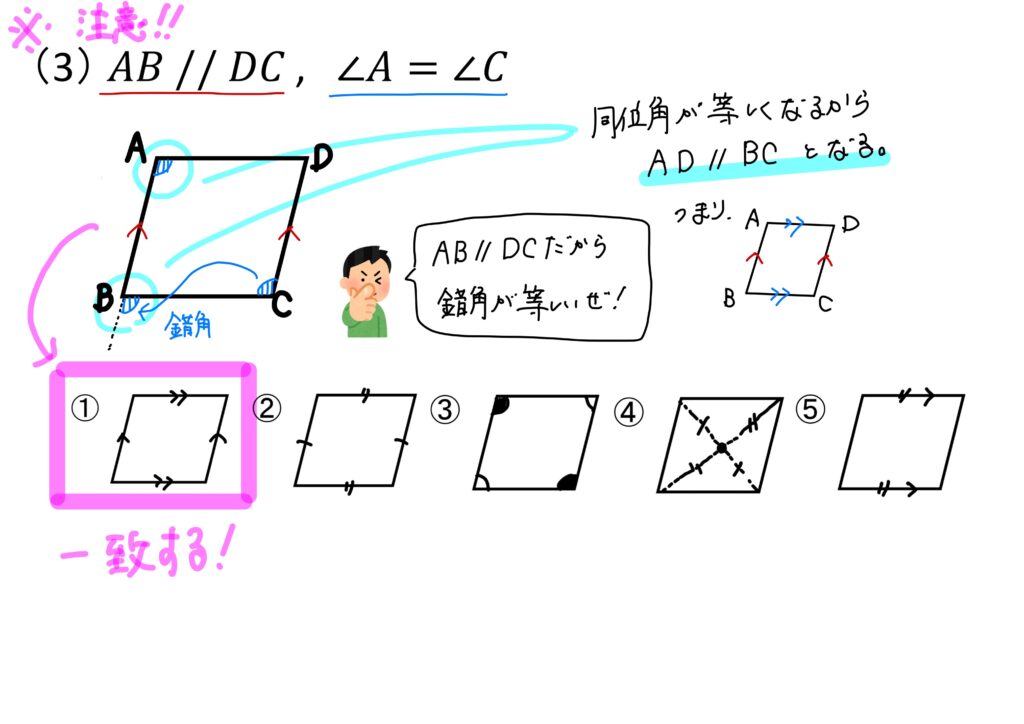
(3)\(AB//DC, ∠A=∠C\)
(4)\(AB//DC, ∠A=∠D\)

まとめ
お疲れ様でした!
これで平行四辺形になるための条件はバッチリかな??
もうバッチリだぜ!という方は、今回の条件を使った証明問題へとステップアップしていきましょう。
最後にポイントまとめておきますね



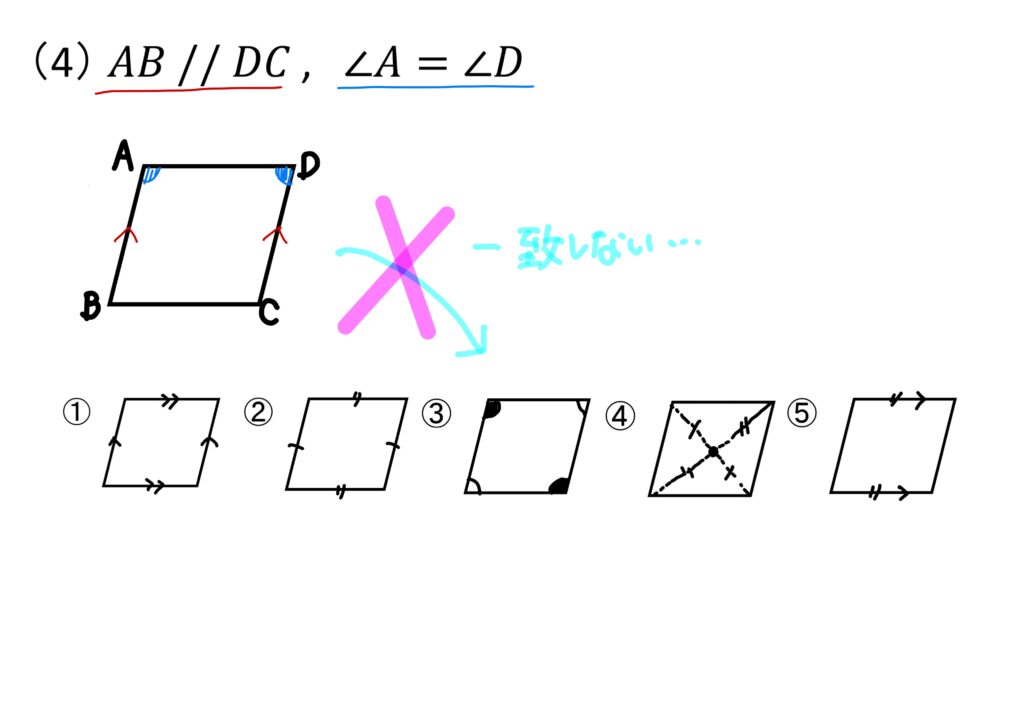












コメントを残す