この形の図形っって
角度を求める問題でよく出てくるよね。
ブーメランの形に似ているから
『ブーメラン型の図形』って呼ばれたりしています。
他にも
矢じり型、矢印型、紙ヒコーキ型 なんて言われていたりもします。
ある女の子が、この図形のことを
アヒルの足！
って言っていてビックリしましたが
この図形の形をどんな風に捉えるかは人それぞれですねｗ
まぁ、それは置いといて
このブーメラン型の図形にはどんな特徴があるかというと
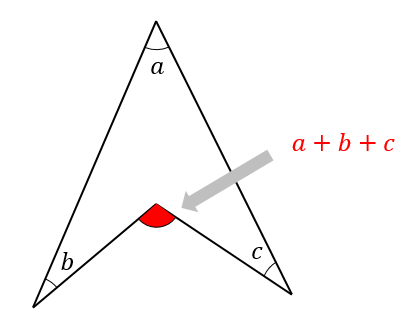
このように
とがっている角を3つ合わせると
凹み部分の角を求めることができるんですね！
これは、とても便利な特徴で
いろんな問題で使えるから覚えておきましょう！
でも…
なんで
とがっている角を全部合わせると
凹みの部分の大きさになるの？？
というわけで
この記事では
- ブーメラン型の特徴はなぜ？
- ブーメラン型の問題に挑戦してみよう！
という2点についてお話をしていきます(^^)
今回の記事はこちらの動画でも解説しています(/・ω・)/
ブーメラン型の特徴はなぜ？？
なぜ
ブーメラン型の図形では
このように3つの角を合わせると凹み部分の角の大きさになるのか？？
これを理解するためには
まず、三角形の外角の性質を知っておく必要があります。
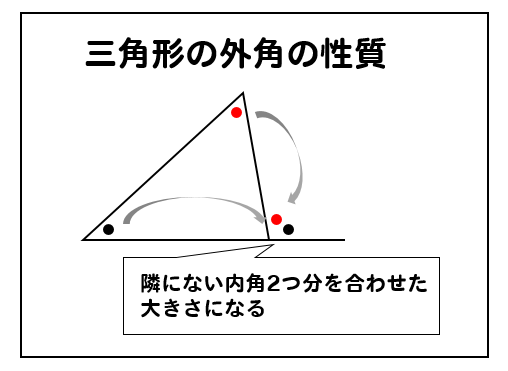
三角形の外角は、隣にない内角2つ分を合わせた大きさと等しくなる
という性質がありました。
この性質を利用しながら
ブーメラン型の図形を見ていきます。
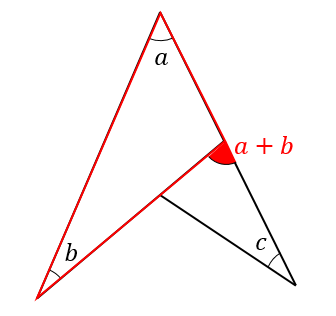
すると、赤い三角形の外角を\(a+b\)と表すことができます。
次に右下にある三角形に注目して
同じように外角を考えると
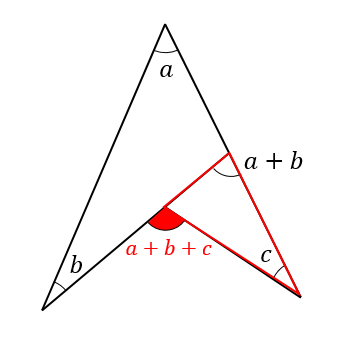
外角の大きさは\((a+b)+c=a+b+c\)と表すことができます。
よって、凹みの部分の角が\(a+b+c\)となるので
とがっている角を全部合わせると凹みの部分の角になるということがわかります。
三角形の外角の性質を利用すると
とがっている角は全部、凹み部分に集めることができるんですね！
それでは、ブーメラン型の角度を求める問題に挑戦してみましょう！
問題に挑戦してみよう！
\(x\)の大きさを求めなさい。
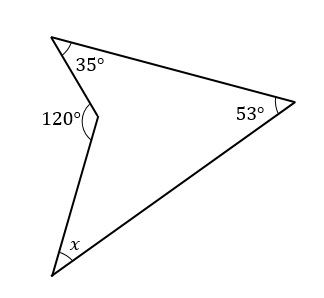
ブーメラン型の図形 まとめ
お疲れ様でした！
ブーメラン型の図形では
この特徴を覚えておけば
問題を解くことは楽勝です(^^)
でも、なんで？？
とツッコミを入れられた場合には
三角形の外角の性質を利用していけば
簡単に説明することができます。
ブーメラン型の図形は
いろんな場面で出題させる問題なので
今のうちにしっかりと覚えて
問題が解けるようにしておきましょう！
ファイトだー(/・ω・)/
星形の図形についてはこちらの記事をどうぞ！
ブーメラン型の角度の求め方！←今回の記事
【証明の書き方】合同な三角形の証明問題の書き方を基礎から解説！
【直角三角形】証明問題の書き方とは？合同条件の使い方を徹底解説！
数スタのオリジナル教材を販売中！
数スタのオリジナル教材を作成しました。
第1弾は高校入試対策、規則性の教材です。
苦手にしている人が多い単元ですが、
コツを掴むと簡単に解けるようになります。
⇒ 【高校入試】規則性の問題をゼロから＋10点する教材
