【連立方程式】鉄橋、トンネルを列車が通過する文章問題はこれでバッチリ！

今回は中２で学習する連立方程式の単元から

列車が鉄橋、トンネルを通過するときの文章問題について解説していくよ！

列車の通過問題というのはこんなやつだね。

この問題では、列車がトンネルや鉄橋を通過するというのはどういうことなのか。

そのポイントを知っておく必要があります。

トンネル・鉄橋を通り抜けるときのポイントとは

列車がトンネルや鉄橋を通り抜けるというのは、どういうことか考えていきましょう。

まず列車がトンネルや鉄橋を渡り始めるというのは、列車の頭がトンネルの入口に差し掛かった状況のことをいいます。

そして、列車がトンネルを通り抜けるというのは、列車のお尻部分がトンネルの出口まで到達した状況のことをいいます。

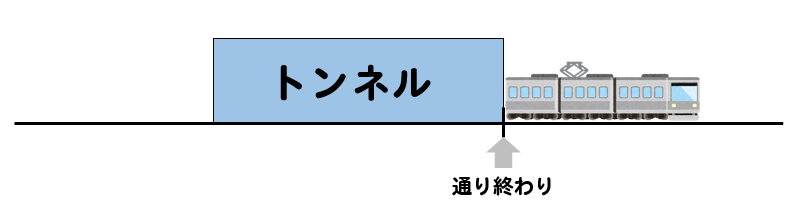
つまり

列車がトンネルや鉄橋を通り抜けるというのは

列車の頭が入口に差し掛かったところから

お尻部分が出口に到達するところまで進んだ状況のことをいいます。

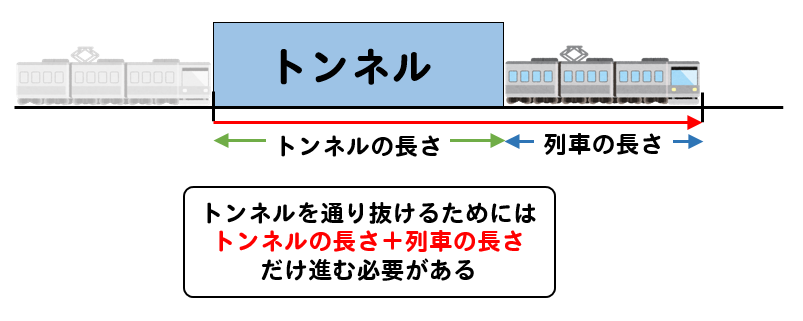
よって、トンネルや鉄橋を通過するためには

（トンネル・鉄橋の長さ）＋（列車の長さ）

だけ列車が進む必要があるということになります。

今回の問題解説！

それでは、上で紹介したポイントを利用して

今回の問題を解説していきます。

まずは、トンネルから考えていきましょう。

このとき、列車は秒速\(y\)mで78秒間進んでているので

\(y\times 78=78y\)だけ進んだことになります。

また、トンネルを通り抜けるまでに列車は

トンネルの長さ＋列車の長さ　の分だけ進む必要があります。

つまり、\(1400+x\)進まなくてはいけません。

よって

$$78y=1400+x$$

となります。

鉄橋の場合も考えましょう。

このとき、列車は秒速\(y\)mで35秒間進んでているので

\(y\times 35=35y\)だけ進んだことになります。

また、鉄橋を渡りきるまでに列車は

鉄橋の長さ＋列車の長さ　の分だけ進む必要があります。

つまり、\(540+x\)進まなくてはいけません。

よって

$$35y=540+x$$

となります。

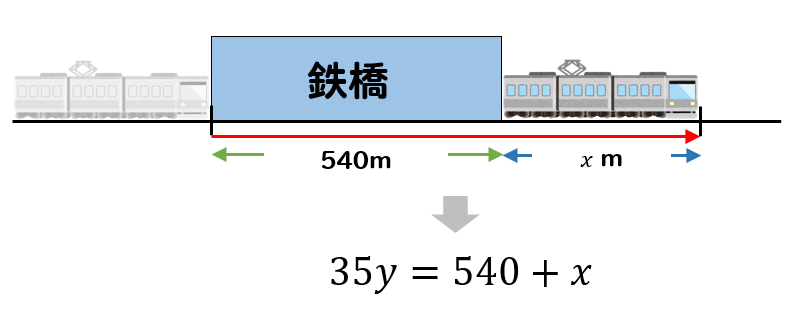
2つの式をまとめると

$$\begin{eqnarray} \left\{ \begin{array}{l} 78y = 1400+x \\ 35y = 540+x \end{array} \right. \end{eqnarray}$$

このような連立方程式を作ることができました。

あとは計算していくだけですね！

今回は代入法を使って計算していきます。

それぞれ\(x=\)の形に変形して、代入していきます。

$$78y-1400=x$$

$$35y-540=x$$

$$78y-1400=35y-540$$

$$78y-35y=-540+1400$$

$$43y=860$$

$$y=20$$

\(y=20\)を\(x=35y-540\)に代入すると

$$x=35\times 20-540$$

$$x=700-540$$

$$x=160$$

よって、列車の長さは160m、速さは秒速20mということが求まりました。

列車の長さがポイント！いろんなパターンを学ぼう！

それでは、通過に関しての基本問題はご理解いただけましたね。

ここからは、いろんなパターンを見ていきましょう。

トンネルに隠れていたときを考えるパターン

『トンネルを通過したとき、電車は52秒間トンネルにかくれてその姿が見えなかった。』

トンネルの中で隠れていたというのは

列車のお尻部分がトンネルの入り口を通過してから列車の頭部分がトンネルの出口に差し掛かるまでのことを言います。

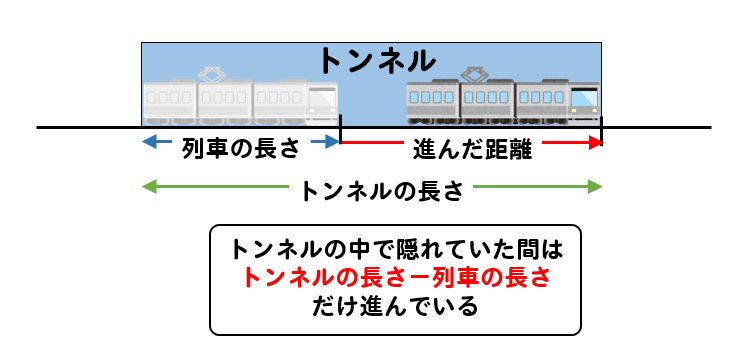
よって、式は

$$52y=1356-x$$

となります。

トンネルを入り始めてから、入りきるまでのパターン

『ある列車がトンネルに入り始めてから、入りきるまでに6秒かかった。』

トンネルの中に入りきるというのは

列車の頭部分がトンネルの入り口を通過してから列車のお尻部分がトンネルの入口に到達するまでのことを言います。

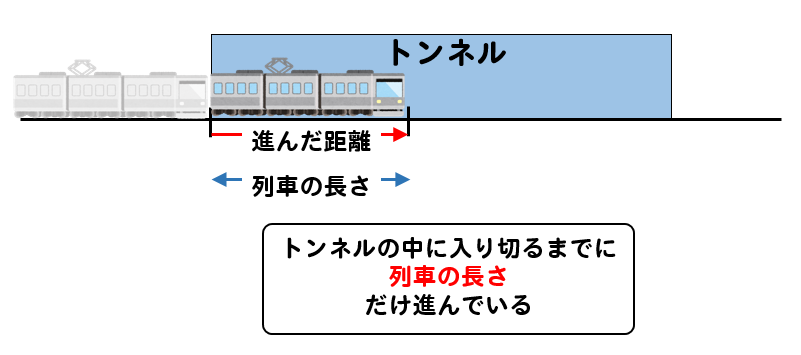
よって、式は

$$6y=x$$

となります。

まとめ

お疲れ様でした！

いろんなパターンを見てもらいましたが

トンネルや鉄橋を通過する問題では

列車の長さを意識することがポイントとなります。

文章だけではなかなかイメージがしにくい問題なので

問題を解くときには簡単な絵を描いてみると

式が立てやすくなるのでおススメです(^^)

それでは、最後にもう1度それぞれのパターンの絵を確認して終わりにしましょう！