【高校入試】関数の頻出パターンを徹底解説！　

関数の問題がニガテ…

だけど、関数って入試にめっちゃ出るじゃん（泣）

 

という方のために、高校入試によく出題される関数のパターン、ポイントをまとめていきます。

関数の勉強、何やったらいいか分からん…って人は参考にしてくださいね(/・ω・)/

2点を通る直線の式を求める。

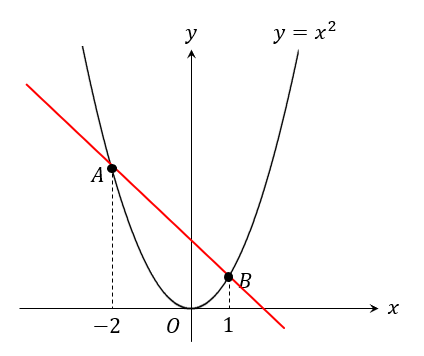
もうね、この問題はめちゃくちゃ出ます！

絶対に解けるようにしておいてください。

 

まずは2点の座標を求めていきましょう。

（最初から座標が与えられている場合もある）

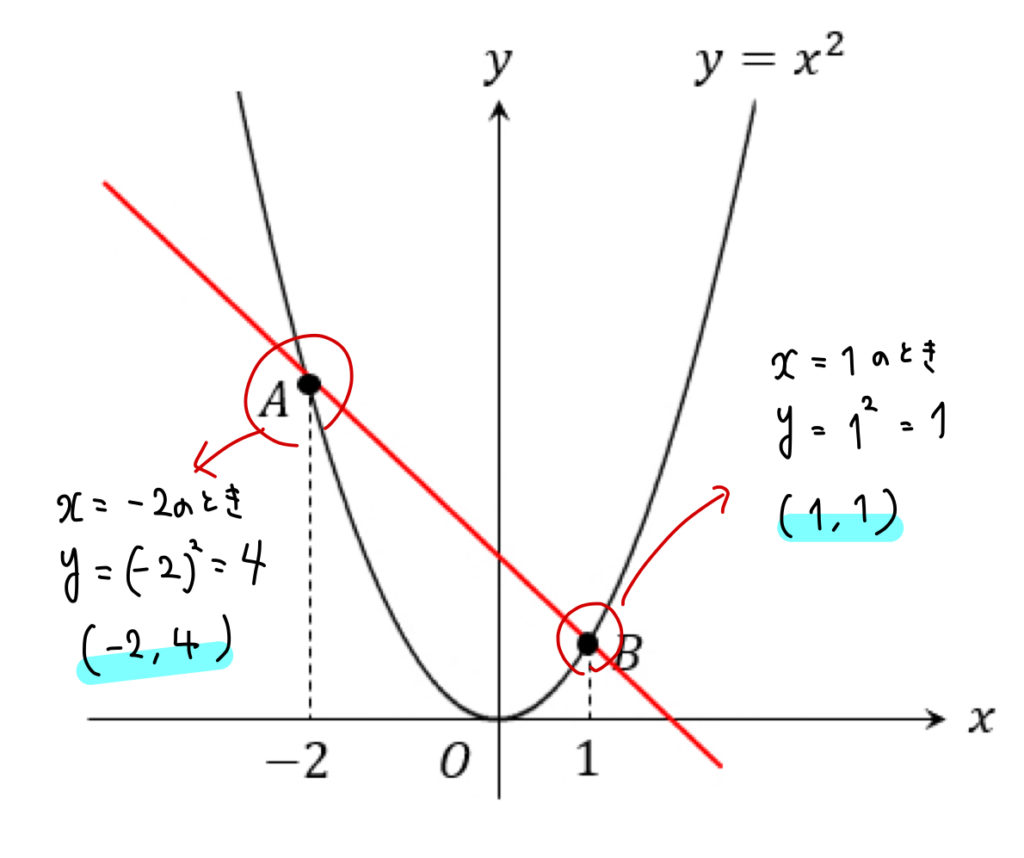
それぞれの\(x\)座標を \(y=x^2\) に代入すると座標が求まりますね。

 

そして、2点の座標が揃ったら

直線の式\(y=ax+b\) に当てはめて計算していきましょう。

 

 

二次関数の\(a\)を求める。

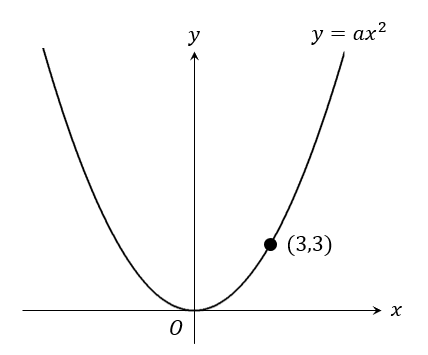
これもよく出題される問題。

とにかく、グラフが通る座標を見つけて代入すればOKです。

 

\(x=3\),\(y=3\)を\( y=ax^2\)に代入すると

$$\begin{eqnarray}3&=&a\times 3^2\\[5pt]3&=&9a\\[5pt]a&=&\frac{3}{9}\\[5pt]a&=&\frac{1}{3}\cdots(解) \end{eqnarray}$$

ただ代入するだけなので、簡単な問題ですね(/・ω・)/

 

これは放物線、反比例のグラフにおいてよく出題される問題。

こちらの記事で復習しておいてくださいね！

 

変域を求める。

 

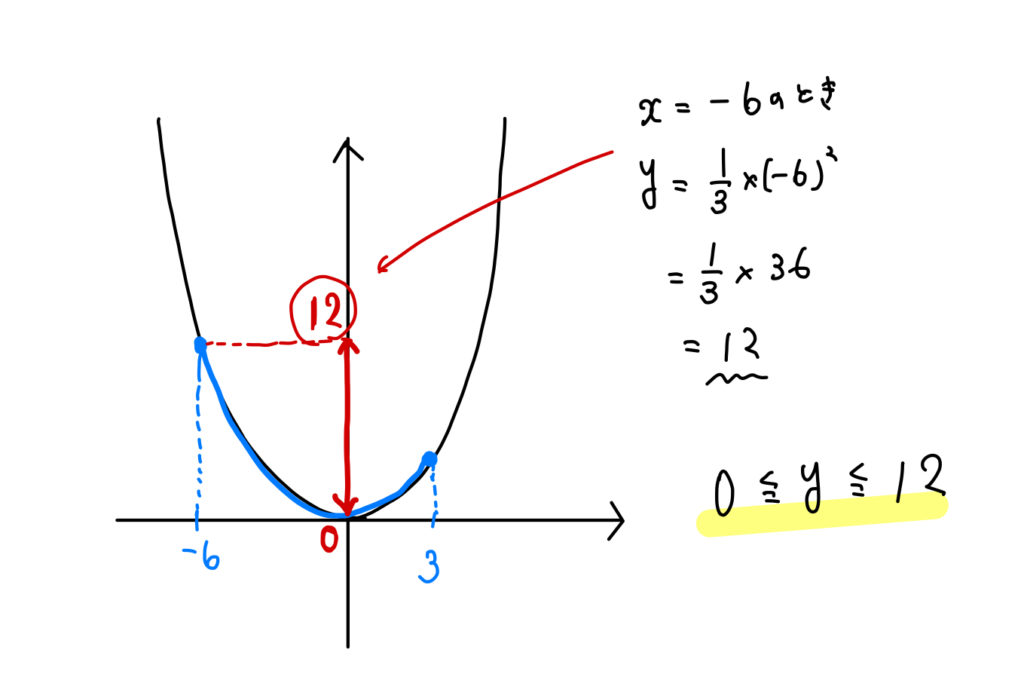
変域の問題もめちゃくちゃ出る！

（変域問題は、ほとんどが放物線）

 

更には、\(x,y\)の変域から関数の式を求めさせる問題もあります。

解き方については、こちらの記事で確認しておきましょう！

変化の割合を求める。

 

関数\(y=ax^2\)については、下のような裏ワザ公式が使えます。

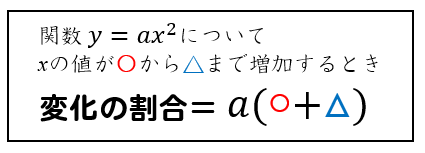
よって、今回の問題では、

$$2\times (-1+4)=6\cdots (解)$$

と解くことができます。

 

公式を覚えておくと、すっごくラクなので

使いこなせるようにしておきましょう(/・ω・)/

 

変化話の割合といえば、一次関数や反比例の場合も出題されます。

こちらの記事で変化の割合についてまとめているので参考に！

長さを求める。

 

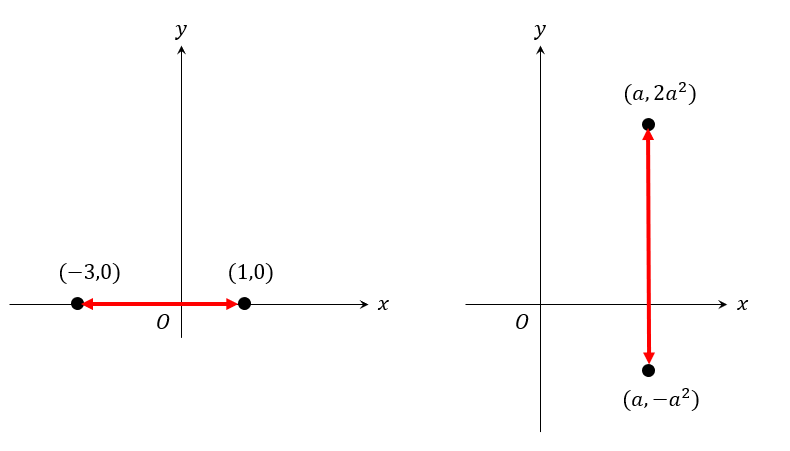
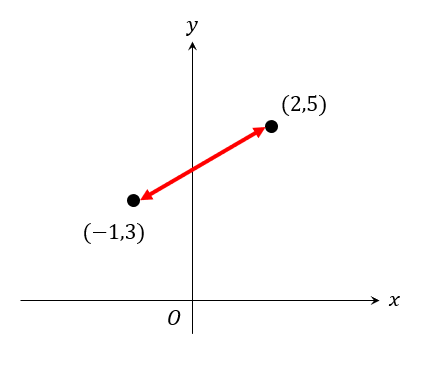
横の長さは、\(x\)座標の大きい方から小さい方を引く。

縦の長さは、\(y\)座標の大きい方から小さい方を引く。

斜めの長さは、三平方の定理を用いて求める。

 

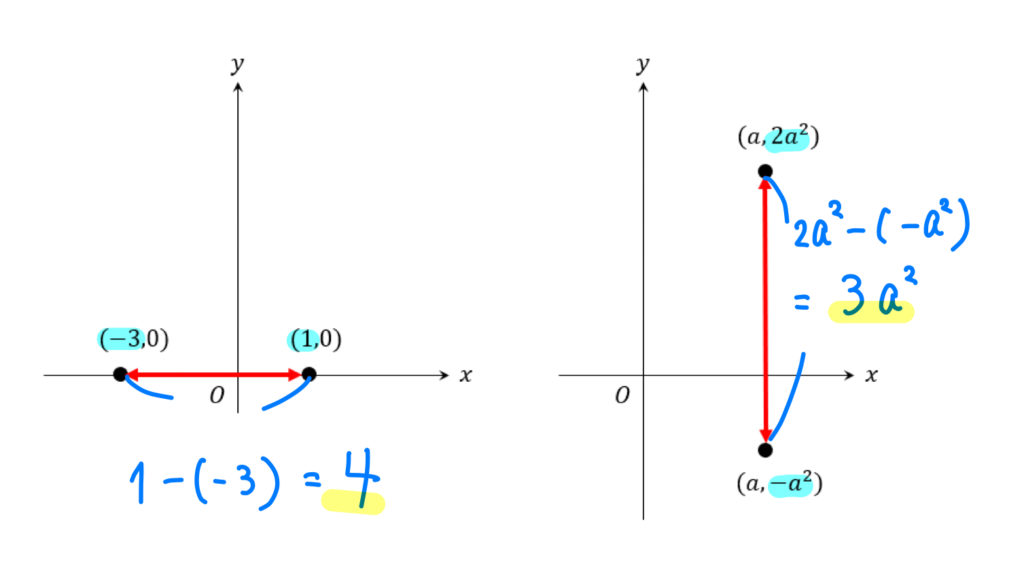
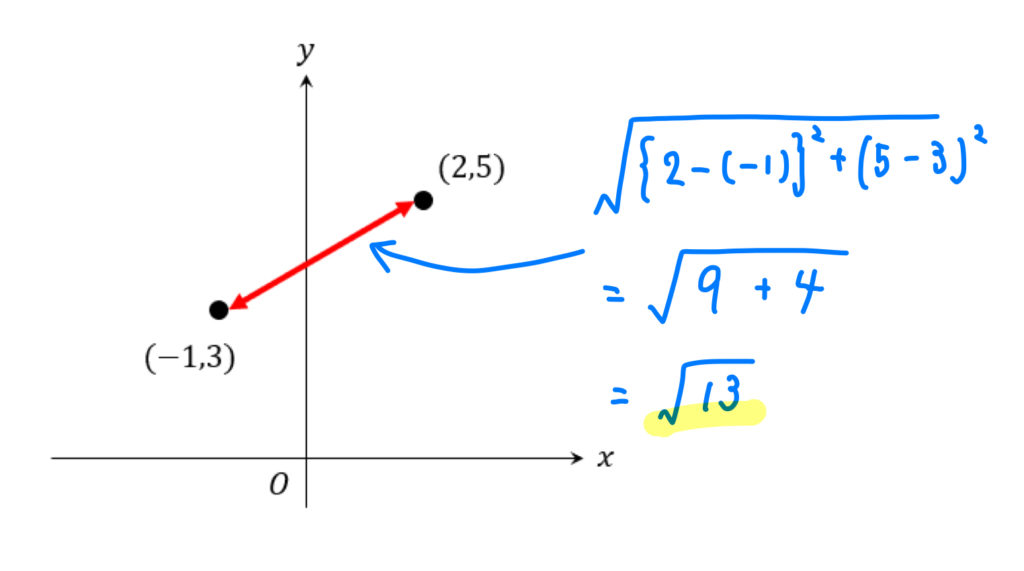
グラフ上の2点の距離を求めさせる問題は多いです。

次に紹介する面積を求める問題では、

長さを求めるという考えが重要になります。

放物線と直線の面積を求める。

 

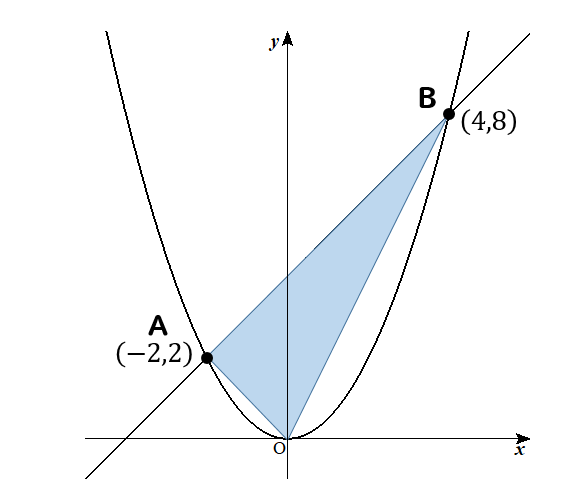
こちらもよく見かけるタイプの問題ですね。

手順は決まっているので、その通りにやっていくだけです。

直線ABの式を求めて、切片を読み取ったあとは

次のように三角形を分割して面積を求めてください。

 

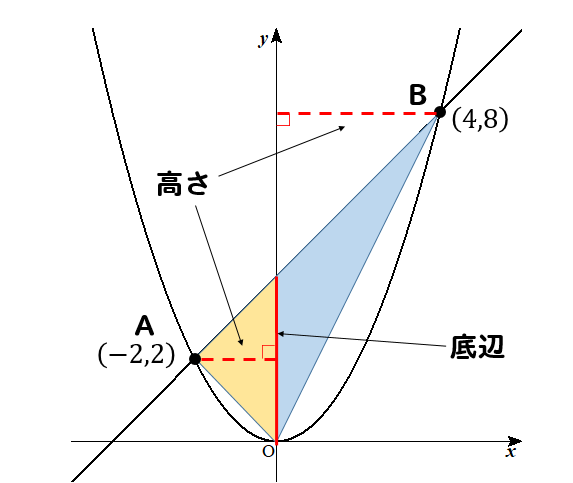
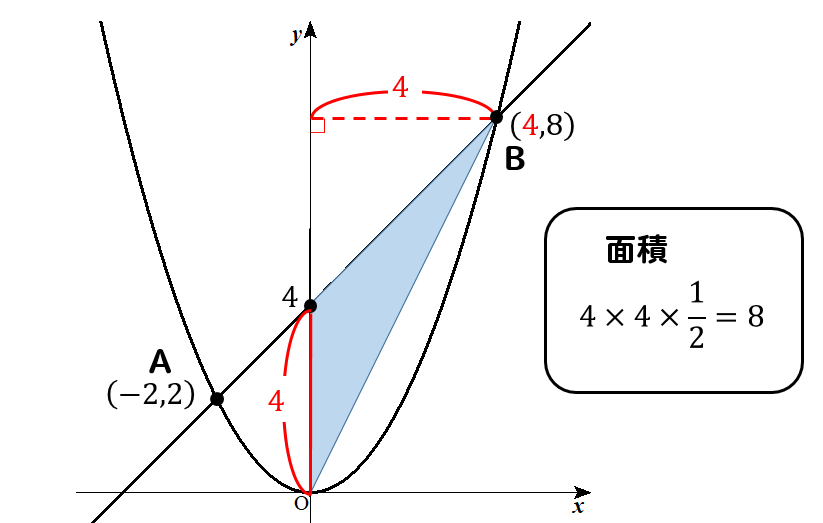
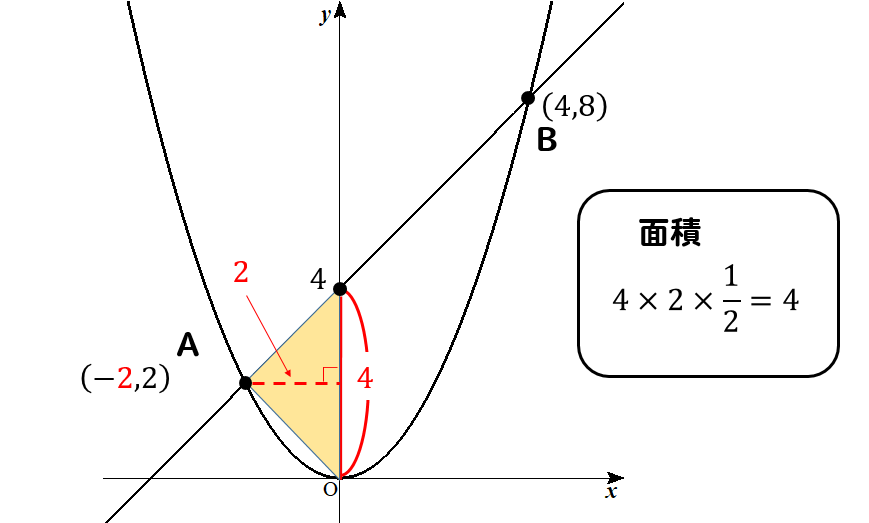
よって、△AOBの面積は、

\(8+4=12\cdots(解)\)　となります。

 

面積を二等分する直線

 

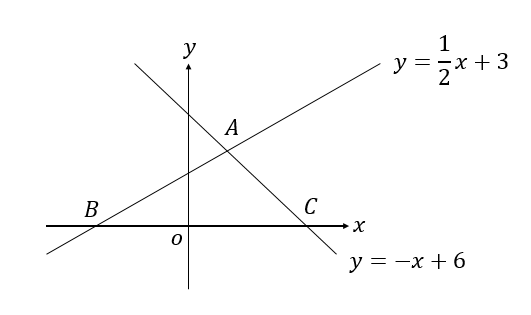
三角形を二等分するためには、

底辺にあたる部分の中点を通ればOK。

 

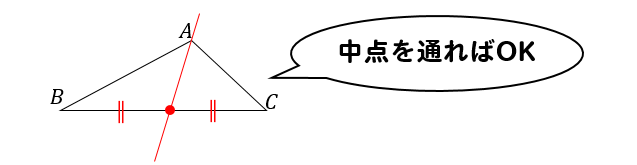
ここでおさえておきたいのが、

中点の求め方です。

意外と知らない方が多いので、覚えておいてください。

このように \(x,  y\)座標をそれぞれ足し、2で割る。

これで中点が求めれます。

 

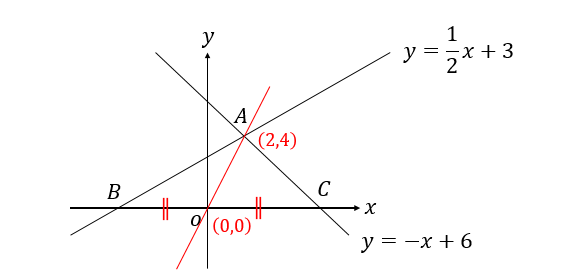
2点\((2,4), (0,0)\)を通るということより

$$y=2x\cdots(解)$$

となります。

 

ちなみに！

平行四辺形を二等分するという問題もよく出題されます。

平行四辺形の場合は、

対角線が交わる点を通るように直線を引くと二等分することができます。

比を考える。

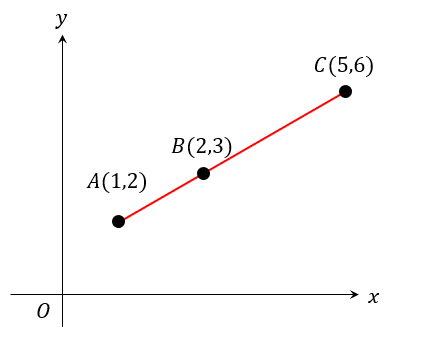
げ…斜めの長さを考えるのか…

と、思うかもしれませんが

次のように考えてみると簡単に比が求まります！

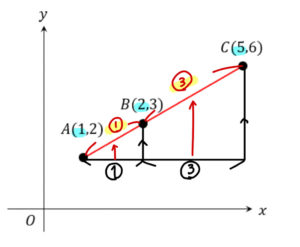
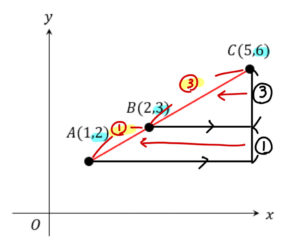
このように直角三角形を作って、平行線と線分の比に注目することで

\(x,y\)座標のどちらかを利用して、斜めの長さの比を求めることができます。

 

よって、線分ABと線分BCの比は、\(1:3\cdots(解)\) となります。

正方形について考える。

 

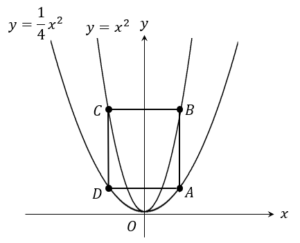
グラフ上にて、正方形を考える問題では次の手順で解いていきましょう！

 

まず、求めたい点Aの\(x\)座標を\(a\)とすると、

それぞれの座標、辺の長さはこのように表すことができます。

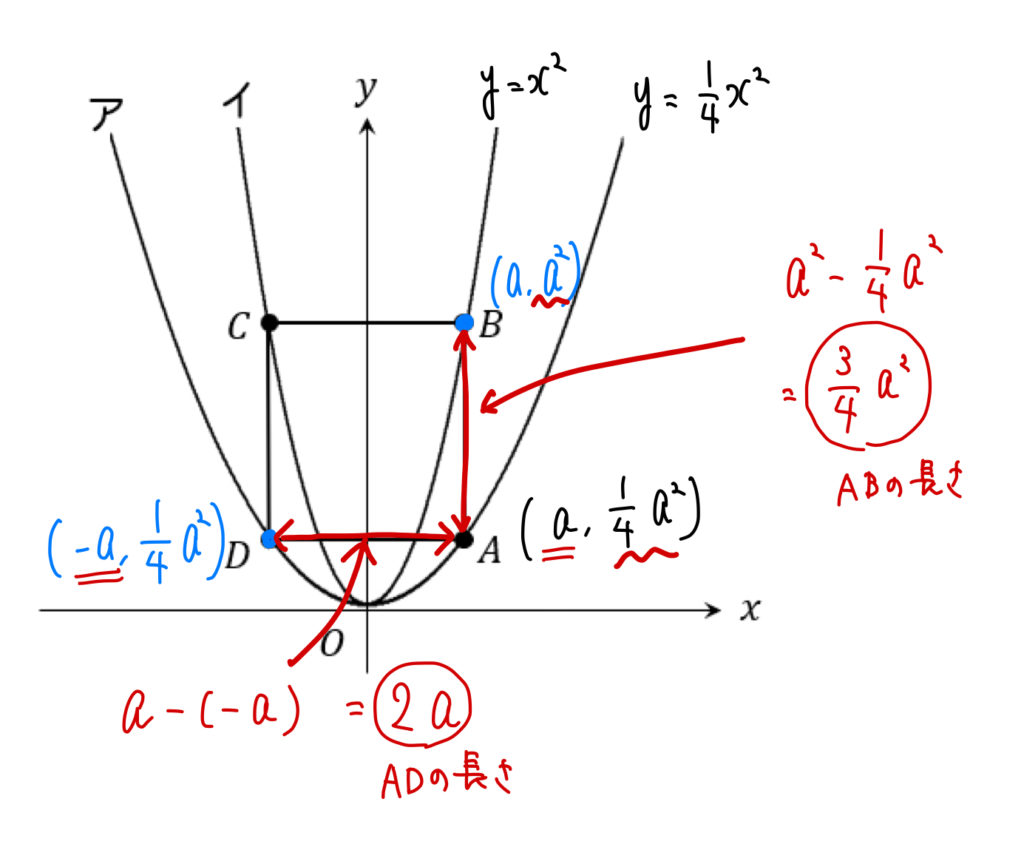
辺AB、辺ADの長さが等しくなれば正方形になるので…

$$\begin{eqnarray}\frac{3}{4}a^2&=&2a\\[5pt]3a^2&=&8a\\[5pt]3a^2-8a&=&0\\[5pt]a(3a-8)&=&0\\[5pt]a&=&0,\frac{8}{3}\end{eqnarray}$$

\(a=0\)のときは、点Aが原点になってしまって正方形が作れなくなるので問題に合いません。

よって、答えは\(\frac{8}{3}\cdots(解)\) となります。

 

等しい面積を求める（等積変形）

 

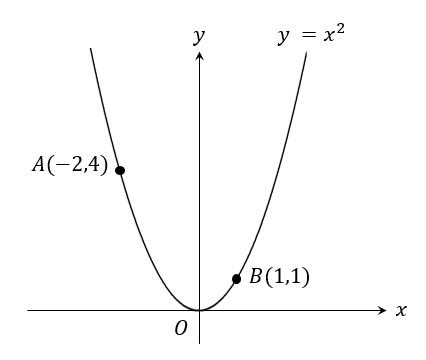
グラフ上で面積の等しい三角形を作る場合

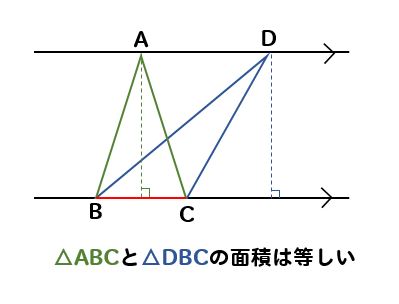
この等積変形の考えを利用することが多いです。

 

今回の問題であれば、点Aを通り直線OBに平行な直線を引き、

その直線が\(x\)軸と交わる点をPとします。

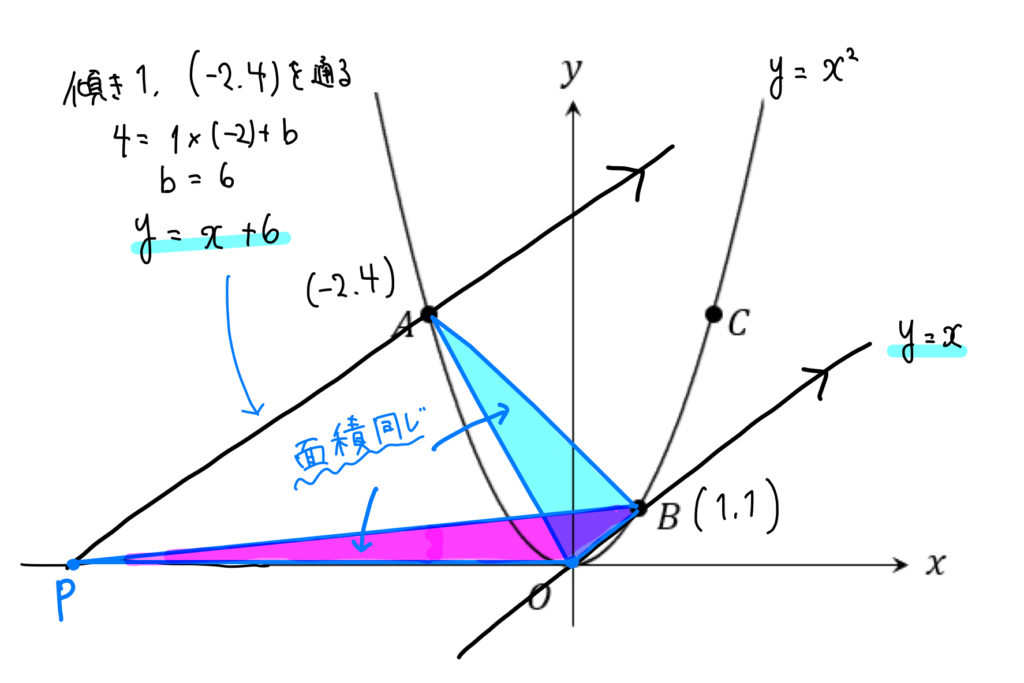
よって、点Pの座標は\(P(-6,0)\cdots(解)\) となります。

 

最短の長さになる点を求める。

 

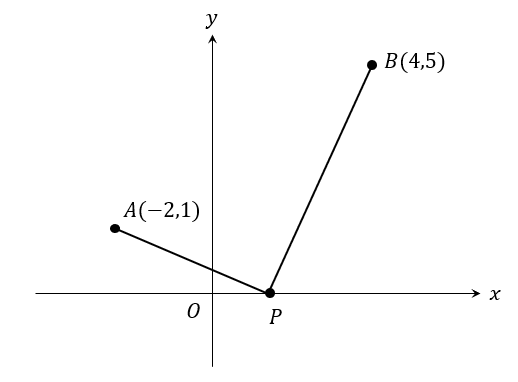
こういった最短を考える問題では、

点A、Bのどちらかを点Pがある\(x\)軸に対して、対称移動した点をとります。

そして、その点ともう一方の点を直線で結びます。

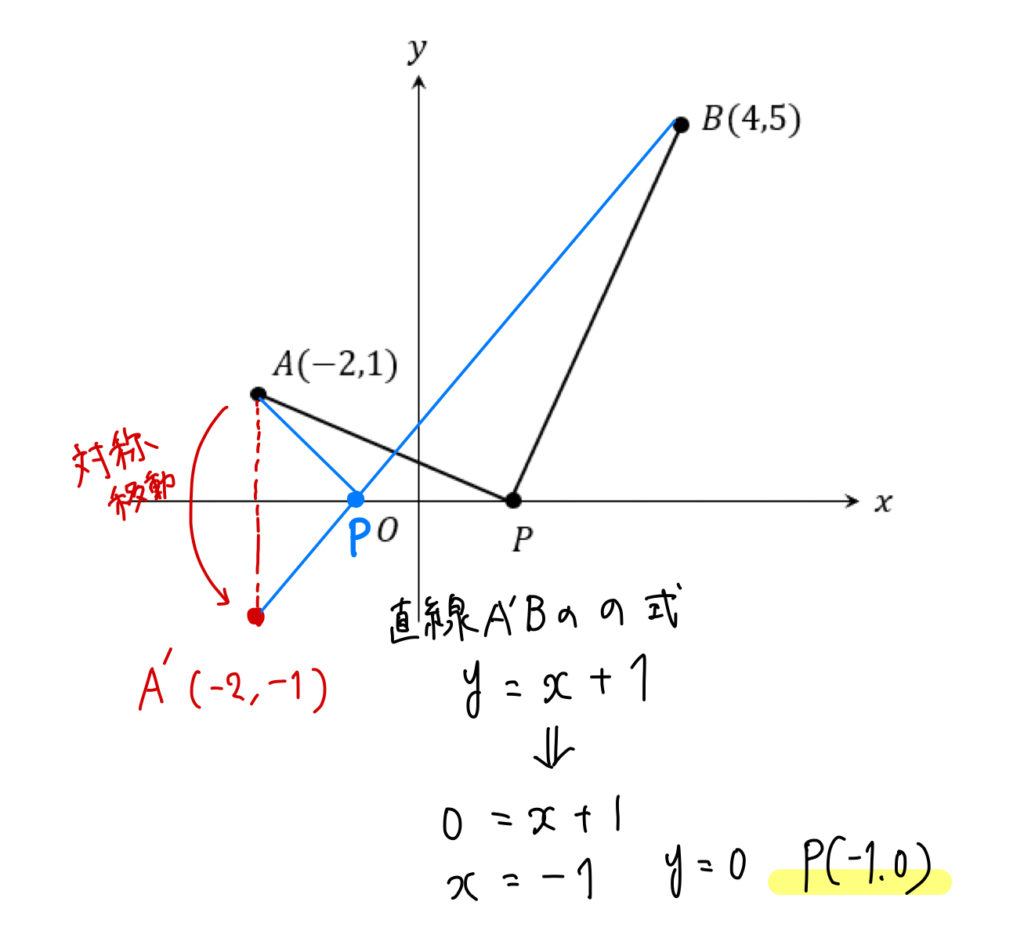
このときに\(x\)軸と交わる点をPとすると、

長さを最小にすることができます。

 

 

この発想は、作図においても利用することがあります。

詳しくはこちらの記事をご参考ください！

垂直な直線

 

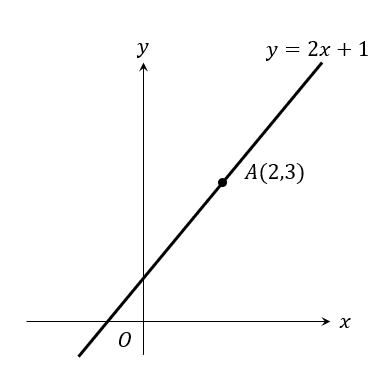
平行といえば、「傾きが等しい」でしたが、

垂直の場合には、傾きがどうなるか知っていますか？

 

垂直の場合には、傾きは

符号チェンジの逆数になります。

具体例をあげておきますね。

 

傾き2に垂直　⇒　傾きは\(-\frac{1}{2}\)

傾き\(-\frac{3}{4}\)に垂直　⇒　傾きは\(\frac{4}{3}\)

 

このように、垂直な直線は

一方の直線の傾きに対して、符号をチェンジして逆数にした値になるのです。

 

このことを覚えていたら簡単に解くことができますね！

 

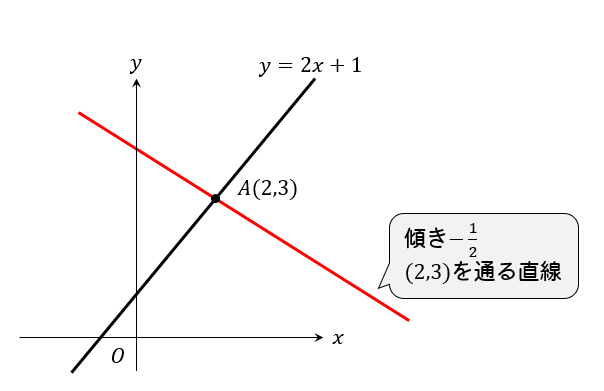
つまり、\(y=-\frac{1}{2}x+4\cdots(解)\) となります。

まとめ！

入試に出やすい知識、パターンについてまとめておきました。

どれも大事なものばかり。

知らなかった、忘れていた…

というものはしっかりと復習しておいてくださいね(/・ω・)/