今回の記事では、高校数学Ⅱで学習する
「展開式の係数の求め方」
について、やり方をイチから確認していきます。
挑戦していく問題はこちら!
【問題】
次の展開式において、[ ]内に指定された項の係数を求めよ。
(1)\((x-2y)^6\) [\(xy^5\)]
(2)\(\left( x+\frac{3}{x}\right)^4\) [\(x^2\)] [定数項]
(3)\((x+y-3z)^8\) [\(x^5yz^2\)]
(4)\((x^2+x+1)^8\) [\(x^4\)]
今回の内容はこちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
二項定理を確認!
二項定理
$$\begin{eqnarray}(a+b)^n={}_n \mathrm{ C }_0 a^n+ {}_n \mathrm{ C }_1 a^{n-1}b+\cdots+{}_n \mathrm{ C }_r a^{n-r}b^r+\cdots {}_n \mathrm{ C }_n b^n\end{eqnarray}$$
\({}_n \mathrm{ C }_r a^{n-r}b^r\) を展開式の一般項といいます。
この一般項を利用して、展開式の係数を求めていきます。
(1)の解説、二項定理を使った基礎問題
【問題】
(1)\((x-2y)^6\) [\(xy^5\)]
こちらを二項定理を使って展開をしていくと、
一般項は次のような形になり、\(xy^5\)になるための\(r\)の値を見つけることができます。
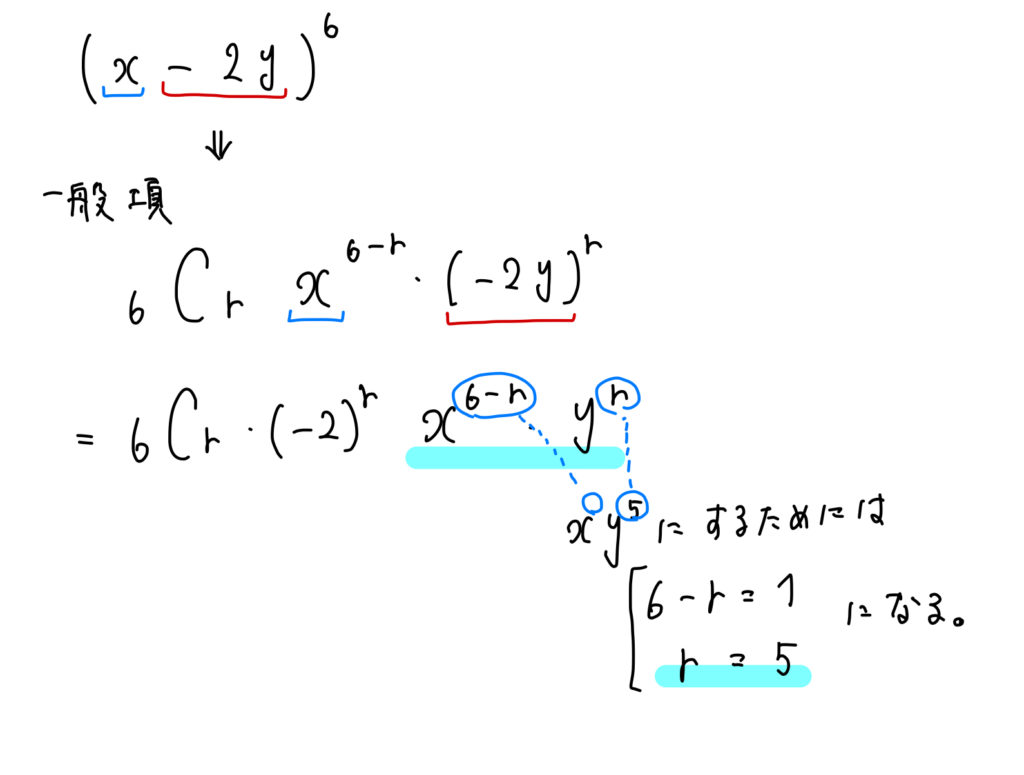
\(r=5\)になることが分かれば、一般項にあてはめて計算をしていきましょう。
$$\begin{eqnarray}{}_6 \mathrm{ C }_5 x^{6-5}\cdot(-2y)^5&=&6\cdot x \cdot (-32y^5)\\[5pt]&=&-192xy^5 \end{eqnarray}$$
よって、\(xy^5\)の係数は\(-192\)であることが求まりました。
答え
$$-192$$
(2)の解説、約分ができるので注意!定数項は?
【問題】
(2)\(\left( x+\frac{3}{x}\right)^4\) [\(x^2\)] [定数項]
まずは、\(x^2\)の係数を考えてみましょう。
こちらも一般項を作って、\(r\)の値を見つけます。
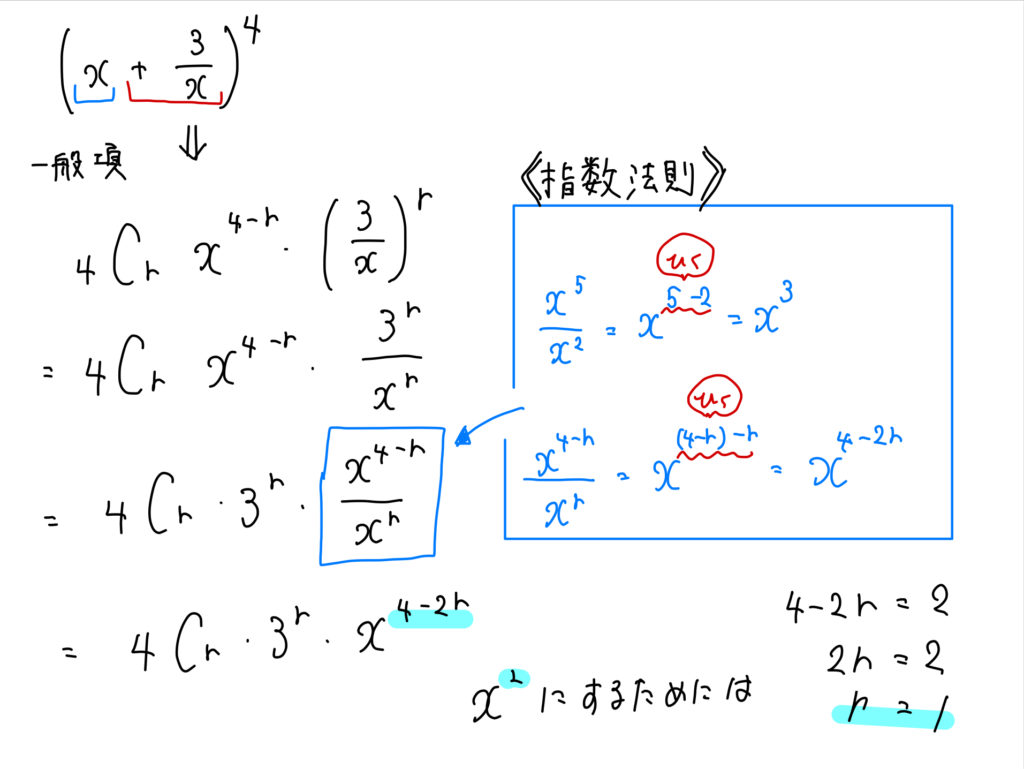
今回の問題のように、分母に文字がある場合には、
一般項を整理するときに約分が必要になります。
ここでの約分は指数法則を利用して、
画像にある通り、(上の指数)ー(下の指数)でまとめていきましょう。
すると、\(r=1\)のときだと分かったので、
$$\begin{eqnarray}{}_4 \mathrm{ C }_1 3^1\cdot x^{4-2}&=&4\cdot3\cdot x^2\\[5pt]&=&12x^2 \end{eqnarray}$$
よって、\(x^2\)の係数は\(12\)であることが求まりました。
次に、定数項について考えてみましょう。
定数項とは、文字がなくなって数だけになっている部分のことですね。
つまり、\(x\)の次数が0になっている項ということになります。
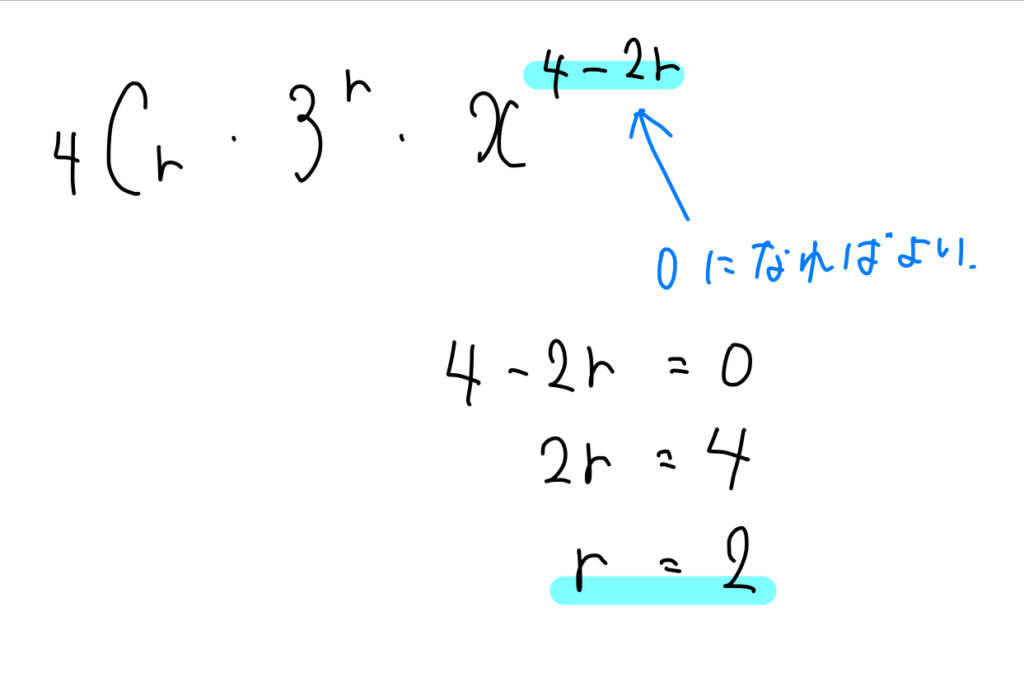
よって、
$$\begin{eqnarray}{}_4 \mathrm{ C }_2 3^2\cdot x^{4-4}&=&6\cdot 9\\[5pt]&=&54 \end{eqnarray}$$
定数項は\(54\)となります。
答え
$$x^2:12 定数項:54$$
(3)の解説、3項ある場合の考え方
【問題】
(3)\((x+y-3z)^8\) [\(x^5yz^2\)]
3項ある場合の一般項は次のように考えます。
\((a+b+c)^n\)の展開式の一般項は
$$\frac{n!}{p!q!r!}a^pb^qc^r$$
$$p+q+r=n$$
よって、今回の式で一般項を作って、\(p,q,r\)の値を求めると次のようになります。
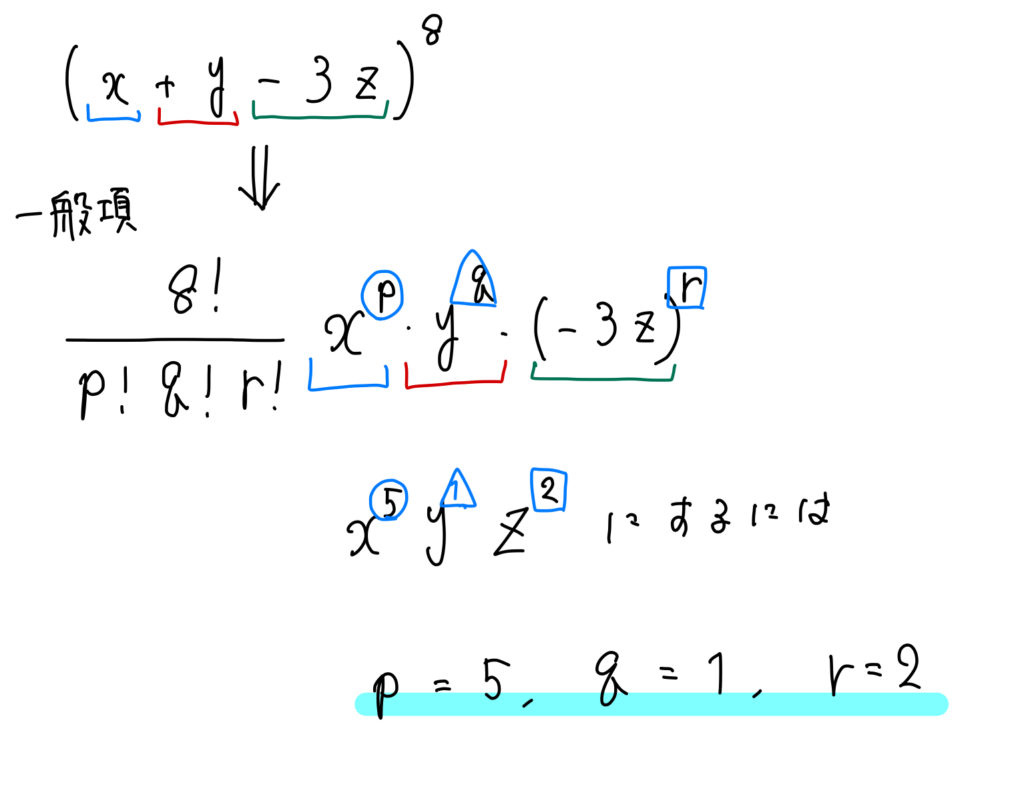
よって、
$$\begin{eqnarray}\frac{8!}{5!1!2!}x^5y^1 (-3z)^2&=&168\cdot x^5y\cdot 9z^2\\[5pt]&=&1512x^5yz^2\end{eqnarray}$$
係数は\(1512\)となります。
答え
$$1512$$
(4)の解説、同じ文字がある場合は?
【問題】
(4)\((x^2+x+1)^8\) [\(x^4\)]
(3)と同じように一般項を作ると、次のようになります。

\(x^4\)にするためには、\(2p+q=4\) になればよいということが分かりました。
更に、\(p+q+r=8\)、\(p≧0,q≧0,r≧0\) であるから
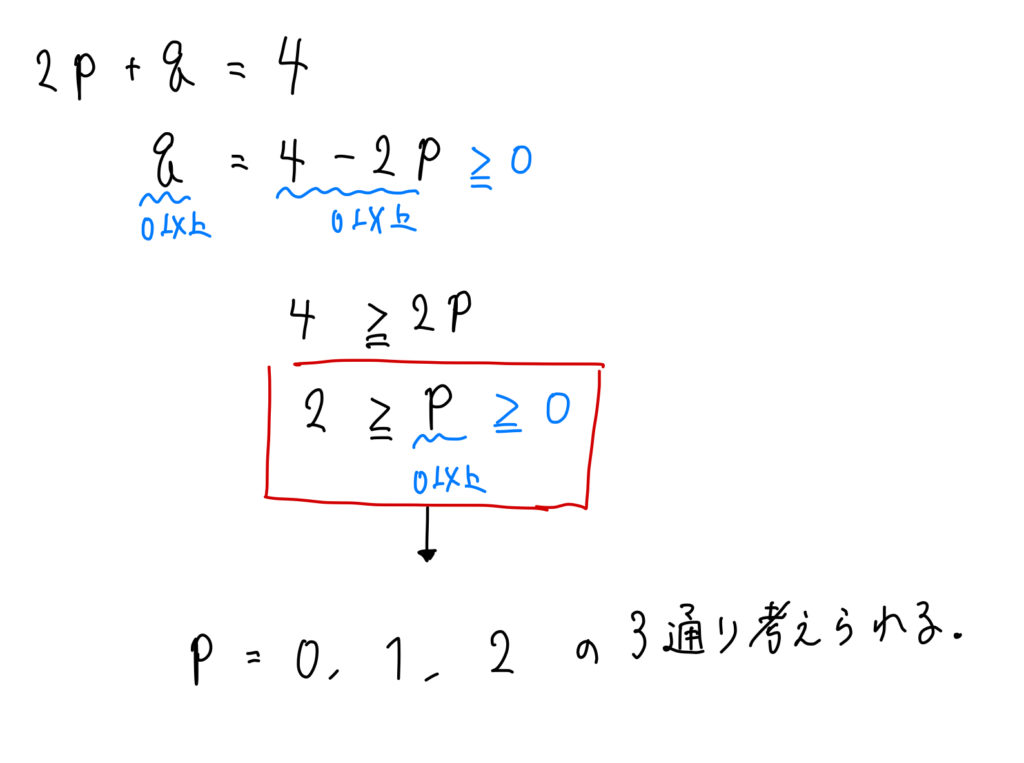
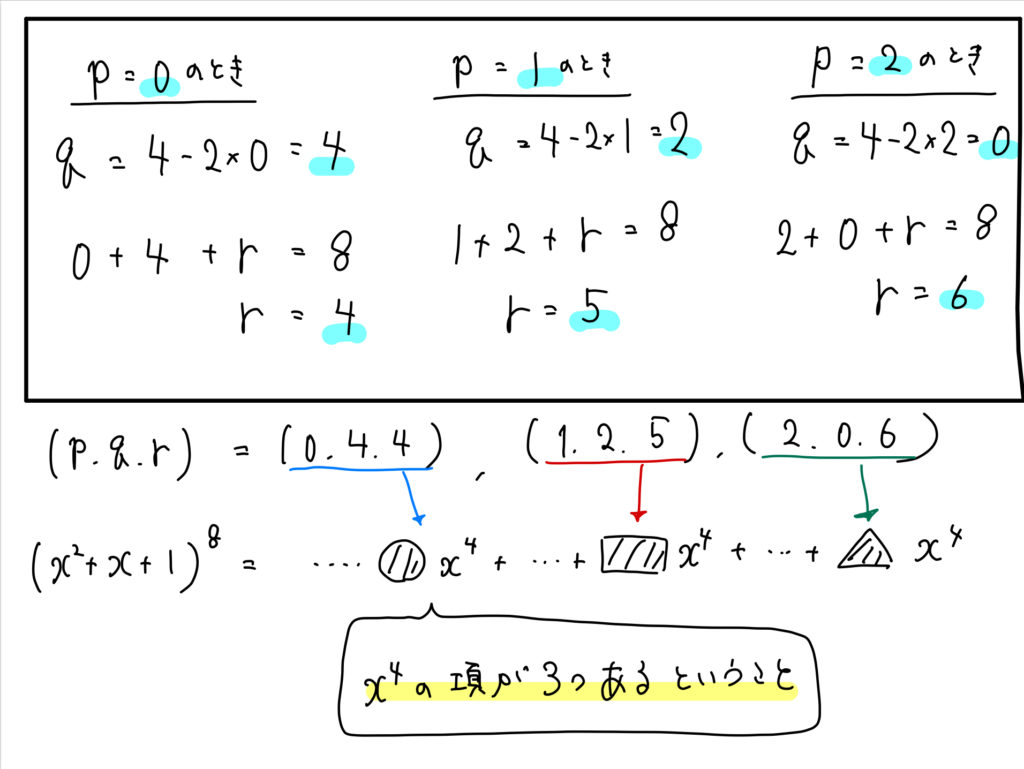
このように、\(p,q,r\)の値を求めます。
今回は\(x^4\)の項が3つ出てくることが分かりましたので、
それらの係数をすべて合わせたものを求めていきましょう。
$$\begin{eqnarray}&&\frac{8!}{0!4!4!}x^4+\frac{8!}{1!2!5!}x^4+\frac{8!}{2!0!5!}x^4\\[5pt]&=&70x^4+168x^4+28x^4\\[5pt]&=&266x^4 \end{eqnarray}$$
よって、\(x^4\)の係数は266だと求まりました。
答え
$$266$$
【課題プレゼント】ちょっと発展的な演習を用意しました!
ここまでのところでそれぞれのパターンの解き方は理解してもらえましたか??
ここからは理解を定着させるための演習課題を用意しました。ちょっと発展的な問題を多めにしておいたので、応用力を高めたい方には必ず解いてもらいたいです。

これらの追加演習にチャレンジして、二項定理を完璧にマスターしたい方には今回の課題&動画解説をメールで送らせてもらっています。あわせて数スタの高校数学の動画講義をまとめた限定サイトもプレゼントしているので、数学の力を伸ばしていきたい方はぜひ活用してくださいね!
【追加演習】二項定理で係数を求める
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用ください^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
まとめ!
お疲れ様でした!
(4)はちょっと難しかったかもしれませんね(^^;)
ですが、どの問題においても展開式の一般項を覚えておくことが大事です。
それぞれの形をしっかりと覚えておきましょう。
\((a+b)^n\)の一般項
$${}_n \mathrm{ C }_r a^{n-r}b^r$$
\((a+b+c)^n\)の一般項
$$\frac{n!}{p!q!r!}a^pb^qc^r$$
$$p+q+r=n$$
















コメントを残す