【高校受験】連立方程式の文章問題！過去問題に挑戦～第3回～

今回は連立方程式の入試問題に挑戦の第3回です。

第1回から学習したい方はこちらからどうぞ(^^)

＞【高校受験】連立方程式の文章問題に挑戦～第1回～

＞【高校受験】連立方程式の文章問題（速さ）に挑戦！～第2回～

やっぱり高校入試に出題される文章問題は

• 割合に関するもの
• 速さに関するもの

この2つが圧倒的に多いですね！

というわけで今回も割合に関する文章問題に挑戦しましょう。

今回挑戦する問題はこちら！

問題のポイント！

今回の問題では、〇割という表現を正確に表すことができるかどうかですね。

詳しくはこちらの記事をご参考いただきたいのですが

＞【文字式】割合（パーセント）の問題をわかりやすく解く方法！

簡単におさらいしておくと

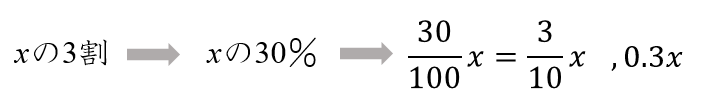
こんな感じでしたね！

〇割を△％に変換して考えていけばOKでした。

それでは、割合の表し方を確認したところで問題の解き方について解説していきます。

問題の答えと解説！

まずは、鉛筆1本の定価を\(x\)円、ノート1冊の定価を\(y\)円として考えていきましょう。

問題文のこの部分から

$$6x+3y=840$$

という式ができあがります。

次に

この部分から式を考えていきましょう。

鉛筆の定価が2割引きということから値段は

$$x\times 0.8=0.8x(円)$$

ノートの定価が3割引きということから値段は

$$y\times 0.7=0.7y(円)$$

それぞれこのように表してやることができます。

そして、割引された鉛筆を10本、ノートを5冊買ったということから代金は

$$0.8x\times 10+0.7y\times 5=8x+3.5y　(円)$$

と表してやることができます。

更に、同じ数量を定価で買った場合の代金は

$$10x+5y　(円)$$

と表すことができます。

それぞれの代金を表すことができたので式を作っていきましょう。

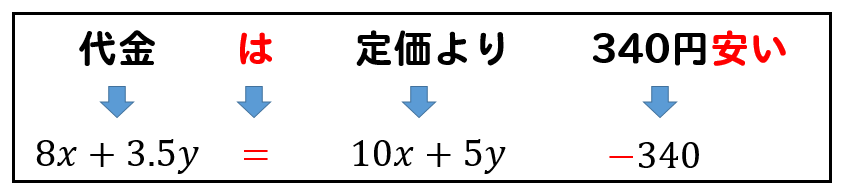
日本語の通り、数式を置いていけば式が完成しますね(^^)

あまり難しく考えず、式を作っていきましょう。

ちょっと式を整理しておくと

$$-2x-1.5y=-340$$

$$2x+1.5y=340$$

$$20x+15y=3400$$

となります。

これで2本の式が完成したので連立方程式を解いていきましょう。

$$\large{\begin{eqnarray} \left\{ \begin{array}{l}6x+3y=840 \\20x+15y=3400 \end{array} \right. \end{eqnarray}}$$

よって

鉛筆1本の定価は80円

ノート1冊の定価は120円となります。

まとめ

お疲れ様でした！

今回の問題では割合を使った数量をちゃんと表せること。

文章から正確に式を作り上げること。

この2点がポイントでしたね！

1度解けてしまえば、そんなに難しい問題ではないですよね(^^)

これで得点アップ間違いなし(・ω・)ノ

と、まぁこんな感じで第3回はおわり！