高校入試対策演習
小問集合の第1回目です!
目安時間は5分です。
挑戦してみましょう(^^)
第1回 小問集合
(1) \(-6+(-15)\div 5\) を計算しなさい。
(2)\(\displaystyle \frac{5x-3}{7}-\frac{x-1}{2}\)を計算しなさい。
(3)\(y\)は\(x\)に反比例し、\(x=5\)のとき\(y=3\)である。\(x=2\)のときの\(y\)の値を求めなさい。
(4)半径が\(6㎝\)、中心角が\(80°\)のおうぎ形の面積を求めなさい。
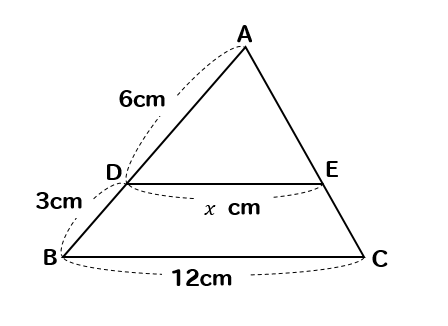
(5)図のような\(△ABC\)があり、\(DE//BC\)である。\(x\)の値を求めなさい。
問題が解けた人は↓で答え合わせをしていきましょう!
こちらの問題はYouTubeでも動画解説しています(/・ω・)/
毎週金曜に、小問演習のプリント&解説動画をお届けしています。
数学の力を伸ばすためには問題演習が欠かせません。
登録は無料ですので、ぜひご活用ください^^
登録直後にこれまでに配信してきた小問課題をまとめてプレゼント。
今すぐ演習にとりかかれますよ!
問題の解答
解答はこちらです。
答え合わせしてみましょう(^^)
答え
(1)\(-9\)
(2)\(\displaystyle \frac{3x+1}{14}\)
(3)\(\displaystyle y=\frac{15}{2}\)
(4)\(8\pi cm^2\)
(5)\(8 cm\)
間違っていた部分は解説を見て
理解を深めておこう!
問題の解説
それでは各問題の解説をしていきます。
間違っていたところは念入りに確認しておきましょう!
(1)の解説!
この問題で気をつけないといけないのは
計算順序!
わり算から先に計算しないといけませんでしたね。

計算順序に気を付けて計算していくと
$$\LARGE{-6+(-15)\div 5}$$
$$\LARGE{=-6+(-3)}$$
$$\LARGE{=-6-3}$$
$$\LARGE{=-9}$$
入試では計算順序で引っかけてくる問題が多いから注意しておきましょう。
(2)の解説!
分数の足し算、引き算では必ず…
通分が必要です!
方程式と勘違いして、分母を払ってしまったり
通分をせずに計算してしまった人はいませんか(._.)
このように間違えてしまう人が多いので入試でもよく出題される問題です。
分母が7と2なので
最小公倍数である14に通分して計算していきます。
$$\LARGE{\frac{5x-3}{7}-\frac{x-1}{2}}$$
$$\LARGE{=\frac{2(5x-3)}{14}-\frac{7(x-1)}{14}}$$
$$\LARGE{=\frac{2(5x-3)-7(x-1)}{14}}$$
$$\LARGE{=\frac{10x-6-7x+7}{14}}$$
$$\LARGE{=\frac{3x+1}{14}}$$
丁寧に一つずつ計算していけば大丈夫です!
途中の式を省いてしまうと符号のミスが起こりやすいので
ポイントは『丁寧に式変形する』ですね。
文字の分数計算が苦手な方はこちらの記事も参考にしてみてください。
(3)の解説!
反比例の式を思い出しましょう。


そして、反比例の比例定数\(a\)は
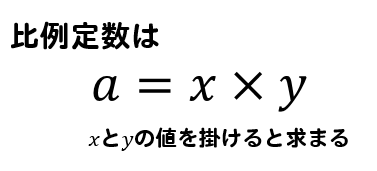
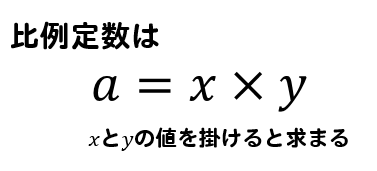
このように\(x\)と\(y\)の値を掛ければ求まりました。
今回の問題では、比例定数は
$$\LARGE{5\times 3=15}$$
よって、反比例の式は
$$\LARGE{y=\frac{15}{x}}$$
となります。
この式に\(x=2\)を代入すると\(y\)の値はいくらになるか?を聞かれているので
$$\LARGE{y=\frac{15}{2}}$$
となりました。
反比例の式を覚えておかないと解けない問題ですが
ちょっと式を覚えておけば、求めること自体はとっても簡単ですね!
(4)の解説!
おうぎ形の公式を思い出しましょう。


面積の公式に当てはめて計算していくと
$$\LARGE{\pi \times 6^2 \times \frac{80}{360}}$$
$$\LARGE{=36\pi \times \frac{2}{9}}$$
$$\LARGE{=8\pi }$$
公式を覚えておけば、当てはめるだけの簡単な問題でした!
おうぎ形の計算は、どうしても分数が出てきてしまうので
分数の計算が苦手な人は何度も演習を繰り返して、慣れておきましょう。
(5)の解説!


これは相似の単元で学習した
平行線と線分の比に関する問題ですね。
\(△ABC\)と\(△ADE\)が相似になっているので
それぞれの比を比べていくと
\(AD:AB=DE:BC\)となるので
$$\LARGE{6:9=x:12}$$
$$\LARGE{9x=72}$$
$$\LARGE{x=8}$$
となります。
平行線と線分の比に関しての詳しい解説はこちらの記事もご参考ください。
以上
小問演習の第1回でした。
全部解けた人は素晴らしい!
解けなかった人も必ず見直しをして
入試本番では解けるようにがんばっていこう!
ファイトだー(/・ω・)/
小問演習~第2回~はこちら























コメントを残す