今回は中学で学習する関数の内容について解説していきます。
グラフの問題を解いていると
点A、B、Cを結んでできる三角形の面積を求めなさい。
直線上の2点A、Bの距離を求めなさい。
というような問題を
一度は目にしたことがあるかと思います。
関数の問題は応用問題になればなるほど
グラフを見ながら、長さを求めなくてはいけないことが増えてきます。
つまり
『グラフから長さを求めることができる』
という力は関数の応用問題を解いていく上で必須なわけです。
そして、今回はそこにスポットライトを当てて
長さを求めることに特化して学習していきたいと思います。
グラフから長さが求めれるようになれば
応用力アップだ!がんばっていこう!
座標から長さを計算する方法~基礎~
座標が与えられているとき
2点間の長さは基本的には
(大きい数)-(小さい数)
で求めることができます。
例えば、これ

1と5
どれくらいの距離があるかといえば
大きい数である5と小さい数である1を引くと
5-1=4
となりますね。
まぁ、これはみなさん体感的に分かる方も多いと思いますが
こうなるとどうでしょうか。
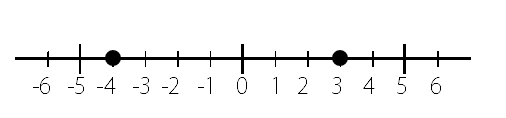
-4と3の距離は
大きい数の3と小さい数のー4を引けばよいから
3-(-4)=3+4=7
となります。
ちょっと分かりにくくなってきましたが
とにかく大きい数から小さい数を引くことですね。
では、さらに発展でこれはどうでしょうか。
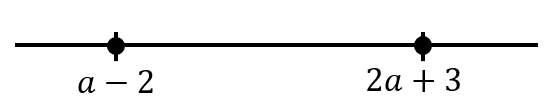
2a+3とa-2の距離を求めろということですが
文字が出てくると感覚的に求めるのが非常に難しくなります。
この場合、(大きい数)ー(小さい数)という計算式が役に立ちます。
つまり
(2a+3)-(a-2)=a+5
となりました。
このように文字を使った複雑な問題もあるので
距離を求めるための基本形式
(大きい数)ー(小さい数)
この形をしっかりと覚えておきましょう。
それでは次に
x軸とy軸のグラフについて考えていきましょう。
グラフから長さを求める 実践編
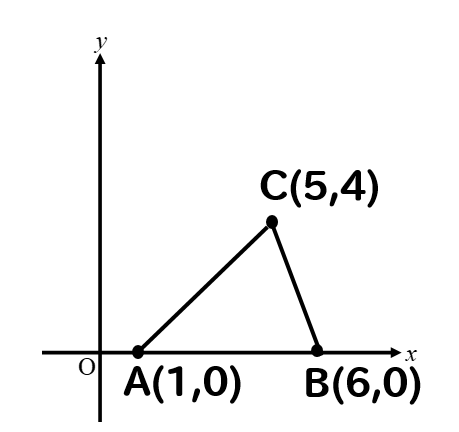
それでは、上のグラフを見て
3点ABCを結んだ三角形の面積を求めたいと思います。
三角形の面積は
(底辺)×(高さ)×1/2
で求めることができるので
まずは底辺部分となるABの長さを求めます。
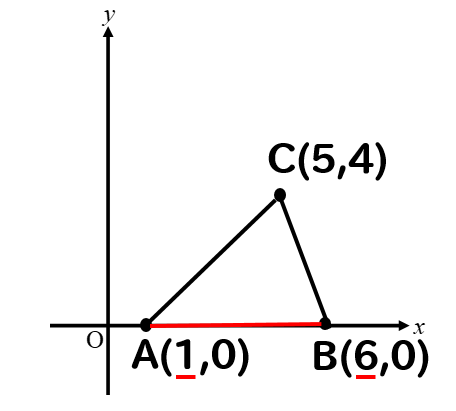
A、Bのx座標を見て
大きい数の6から小さい数の1を引けばよいので
6-1=5
よって、ABの長さは5だと分かります。
次は高さの部分を求めます。
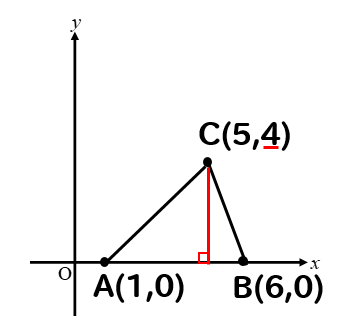
Cのy座標を見れば高さは分かるので
高さは4となります。
これで
底辺5、高さ4
と面積を求めるための情報は揃ったので
5×4×1/2=10 と面積は求めることができました。
とにかく
ここでも(大きい数)ー(小さい数)を活用していきます。
では、文字を使った応用も見ておきましょう。
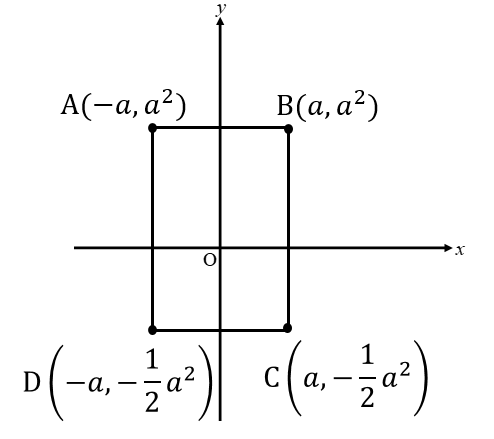
それでは、上のグラフを見て
長方形ABCDの面積を表してみましょう。
長方形の面積を求めるためには、縦と横の長さが必要です。
まずは長方形の横の長さから求めてみます。
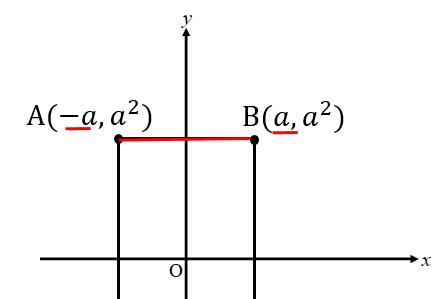
AとBのx座標をそれぞれ見て
大きい数aから小さい数ーaを引きます。
a-(-a)=a+a=2a
これで横の長さ(ABの長さ)が求めれました。
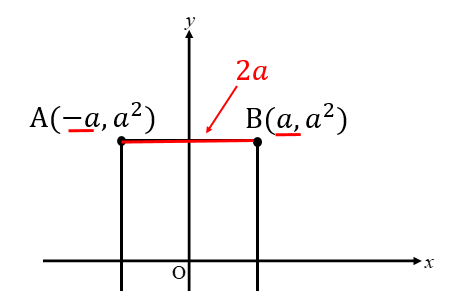
次は縦の長さを求めます。
今度はBとCのy座標をそれぞれ見て
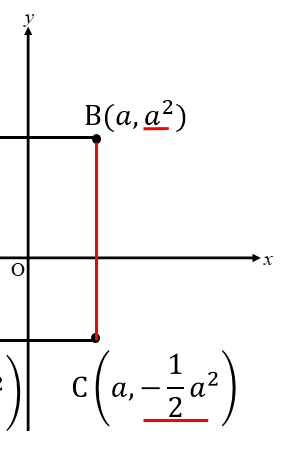
大きい数から小さい数を引いていきます。
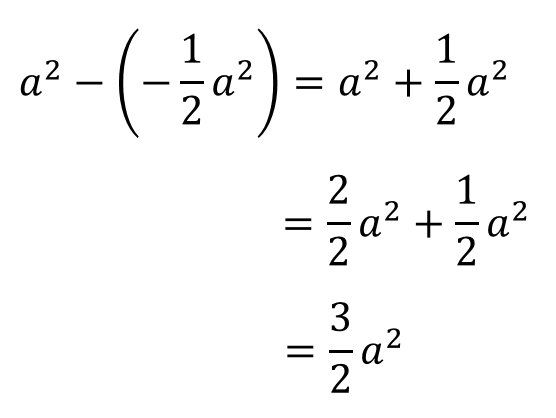
これで縦の長さ(BCの長さ)を求めることができました。
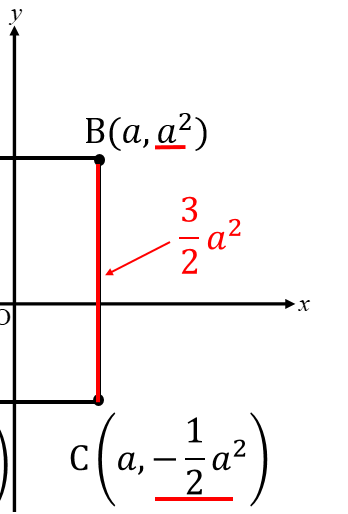
縦と横の長さが揃ったので、面積を求めましょう。
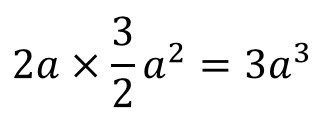
ハイっ!できあがり!
ここでも役に立ったのは
(大きい数)ー(小さい数)
を使って長さを求めることでしたね。
この基本さえ覚えておけば
文字が出てきても大丈夫そうですね!

グラフから長さを求める~発展~
ここからの内容は中3で学習する『三平方の定理』を利用します。
中1、中2生の方は上の実践編までが理解できれば大丈夫です。
では、発展とはどういったものかというと
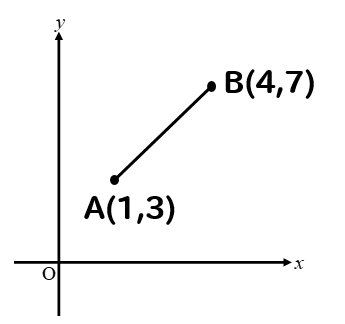
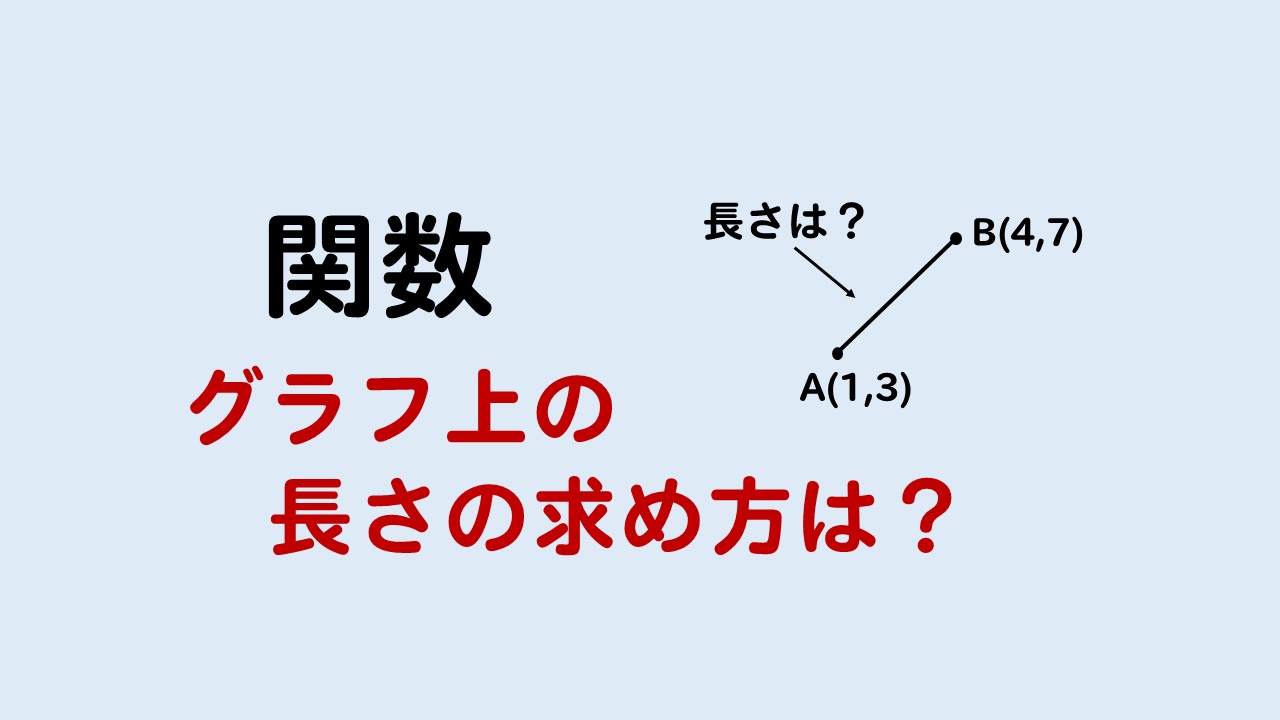
このように斜めに位置しているような2点の長さ(距離)を求めさせるような問題です。
これを解くための手順は
- ABを斜辺とする直角三角形を作る
- 2辺の長さをA、Bの座標から求める
- 三平方の定理で斜辺の長さを求める
このような感じです。
それでは、手順通り見ていきましょう。
① ABを斜辺とする直角三角形を作る
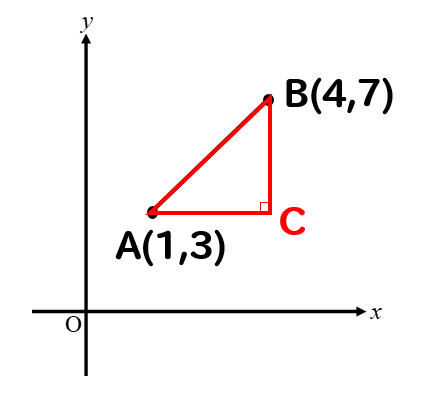
このように直角三角形を作ってやります。
以降の問題解説の為に、直角部分のところをCとしておきますね。
② 2辺の長さをA、Bの座標から求める
直角三角形ができたら、次は長さを求めていきます。
まずはACの長さから
ACの長さはAとBのx座標を見れば良いから
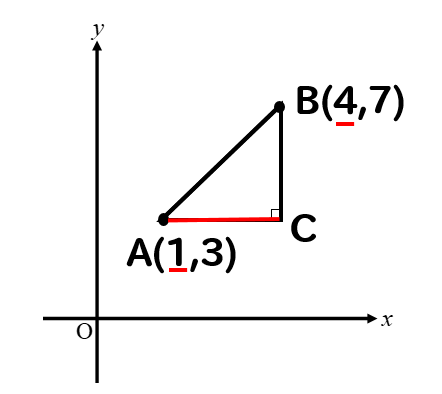
ABの長さは 4-1=3 となります。
次はBCの長さ
今度はAとCのy座標を見ていけば良いから
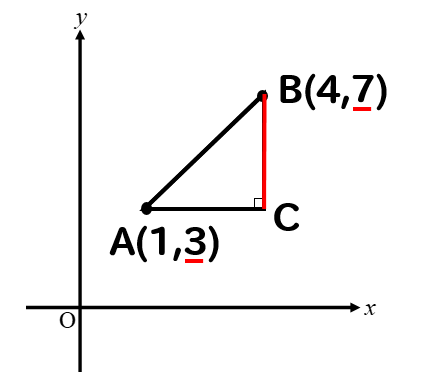
BCの長さは 7-3=4 となります。
③ 三平方の定理で斜辺の長さを求める
直角三角形の2辺が揃ったので
三平方の定理を用いて、斜辺の長さを求めていきます。
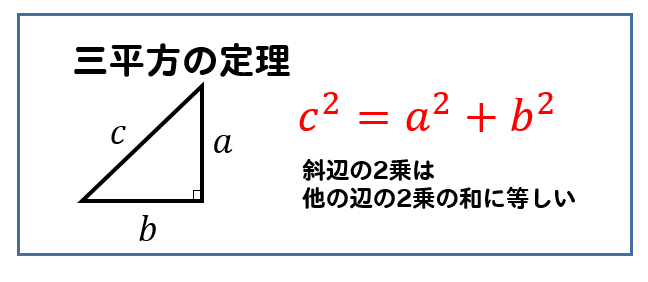
今回はこのような直角三角形なので
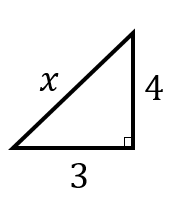
これを三平方の定理に当てはめて計算すると
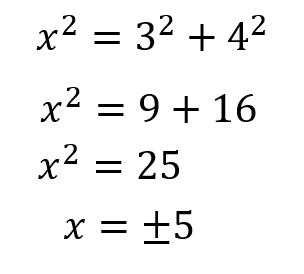
このように求めることができます。
ただし、今回は長さを求めているので
答えが負の数はあり得ないから。
+5が答えとなります。
よって、ABの長さは5となります。
このように斜めの長さを求めるような問題が出てきたとしても
縦、横の長さを基本形にしたがって求めるという点は変わりませんね。
公式使って一発で求めたい人へ
でも、この問題って…
毎回、直角三角形書いて長さ求めるの?
めんどくせーーーーー!!
っていう方は
公式で一発解答する方法もあります。

一見、難しそうにみえますが
横の長さの2乗と縦の長さの2乗の和にルートをつけただけです。
んっと、言葉にしてみてもややこしそうに見えちゃうので
実際に計算してみます。
A(1,3)とB(4,7)の距離を求めたいとき
公式に当てはめてみると
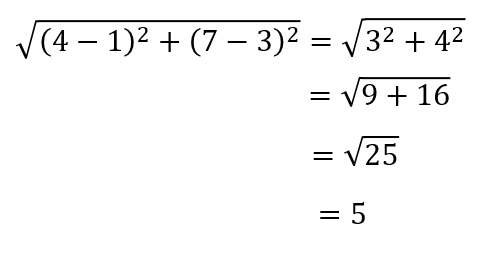
このように求めてやることができます。
慣れたら、圧倒的に楽です。
高校生になると
この公式を使いこなしていくようになるので
今のうちに覚えてしまってもいいかもしれませんね。
もう少し公式に慣れておきたい人のために
いくつか問題を置いておくので挑戦してみてください。
演習問題で理解を深める!
問題
2点A(2,4)、B(5,3)の距離を求めなさい。
問題
2点A(-3,-1)、B(1,-5)の距離を求めなさい。
関数 グラフ上の長さを求める~まとめ~
グラフ上の長さを求めたいときには
座標を見比べて
(大きい数)ー(小さい数)
を計算していけば求めることができます。
斜めの長さになってくると
三平方の定理を利用していくようになりますが

この公式を使いこなして
少しでも楽に計算できるようにしておきましょう。
では!
長さが出せるようになると
応用問題もどんどん解けるようになっちゃうからね
さぁ、演習だー!


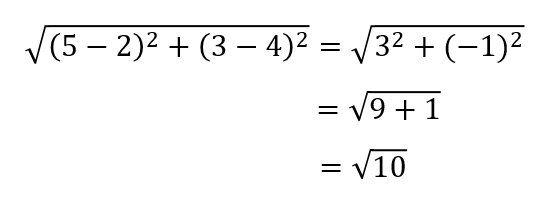
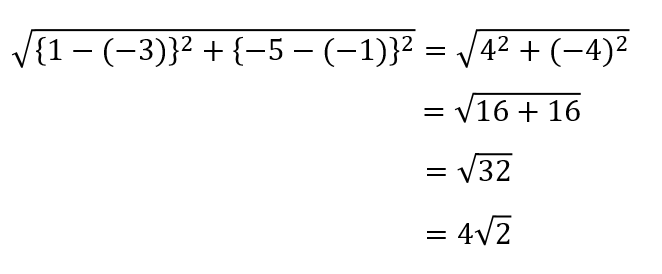














単元テストでこれ見て点上がりました。
ありがとうございます。