今回の記事では、
数学がニガテだ…
でも、階差数列ができるようになりたい!
という方に向けて、階差数列を使った問題についてイチから解説していきます。
なるべく難しい言葉や式は使わずに説明をしていきますので、
最後までがんばっていきましょう!
今回の内容はこちらの動画でも解説しています。サクッと理解したい方は参考にしてくださいね^^
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
階差数列とは?
こちらの数列を例に考えてみましょう!
$$2, 5, 10, 17, 26, 37, \cdots$$
この数列は、\(3, 5, 7, 9, \cdots\) と増えていっていますね。
この増減していく数(隣り合う2項の差)に注目して、
これを書き並べたものを階差数列といいます。
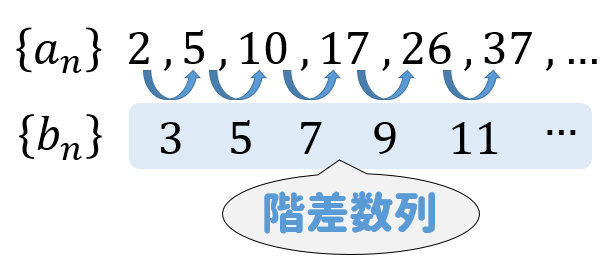
階差数列は、\({b_n}\) という文字を使って表すことが多いです。
そして、\( 2, 5, 10, 17, 26, 37, \cdots\) のように、
等差、等比でもない数列の一般項を考える場合
この階差数列が役に立つことがあります。
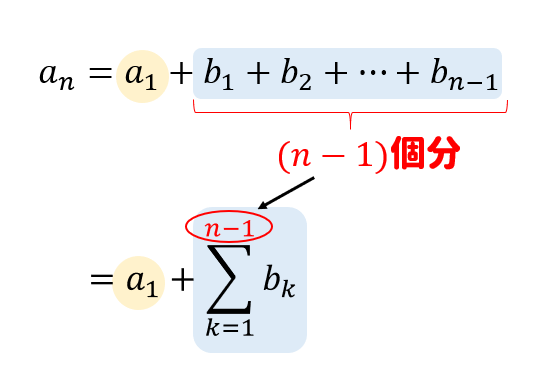
例えば、\(a_5\)という項を階差数列を使って考えると、

\(a_5\)の項は、初項(\(a_1\))に階差数列の\(b_1\) から\(b_4\) までを加えたもの
と考えることができますね。
ポイントは、\(a_5\)の項では、
加える階差数列は4項までです。
図を見たら理解できるとは思いますが、
間違っても\(a_5\) と同じ5項とはしないでくださいね。
同様に考えてみると、
\(a_{10}=a_1+(b_1+b_2+\cdots +b_9)\)
\(a_{20}=a_1+(b_1+b_2+\cdots +b_{19})\)
\(a_n=a_1+(b_1+b_2+\cdots +b_{n-1})\)
と表すことができます。
これをΣを使って書きかえると、
階差数列を使って一般項を求める公式ができあがりです。
ただし、この公式が使えるのは
\(n≧2\) のときに限られます。
\(n=1\) のときには…
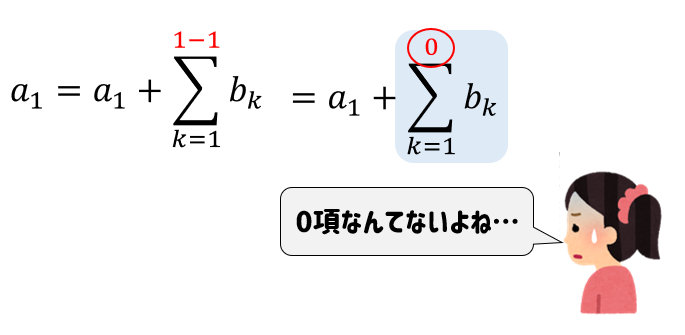
こんな困ったことになっちゃうもんね(^^;)
じゃぁ、\(n=1 \)のときはどーすんの?
って話は次の章にてお話をしていきますね!
【階差数列を使って一般項を求める公式】
数列\(\{a_n\} \) の階差数列を\(\{b_n\}\) とすると、
\(n≧2\) のとき
$$a_n=a_1+\displaystyle \sum_{ k = 1 }^{ n-1 } b_k$$
階差数列を使って一般項を求める
次の数列の一般項を求めよ。
$$2, 5, 10, 17, 26, 37, \cdots$$
パッと見たときに、等差でも等比数列でもありませんね。
こういった場合には、階差数列に注目してみるとよいです。

このように階差数列の一般項が簡単に表せる場合には、
\(n≧2\) のとき
$$a_n=a_1+\displaystyle \sum_{ k = 1 }^{ n-1 } b_k$$
こちらの公式に当てはめて、一般項を求めていきましょう。
ただし、先ほどの章でも言いましたが、
こちらの公式が使えるのは、\(n≧2\) のときだけです。
なので、公式を使うときには事前に、
「\(n≧2\) のとき」を記述しておくようにしましょう。
\(n≧2\) のとき
$$\begin{eqnarray}a_n&=&a_1+\displaystyle \sum_{ k = 1 }^{ n-1 } b_k\\[5pt]&=&2+\displaystyle \sum_{ k = 1 }^{ n-1 }(2k+1)\\[5pt]&=&2+2\displaystyle \sum_{ k = 1 }^{ n-1 }k+\displaystyle \sum_{ k = 1 }^{ n-1 }1\end{eqnarray}$$
ここまできたら、あとはΣの計算をやっていきましょう。
って話になるのですが、ちょっと注意です。
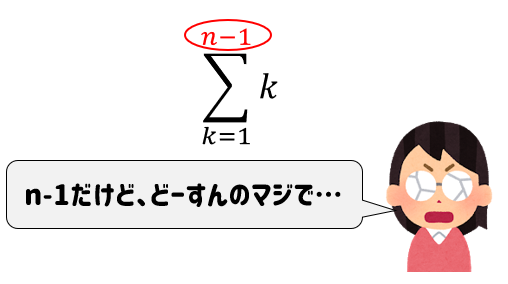
と、Σのところに\((n-1)\)とあるために、
普通のΣの公式とは、ちょっとだけ違った計算になります。
今まで覚えてもらったΣの公式。
これらをすべて\(n ⇒ n-1\) に変えた形で計算をしていく必要があります。
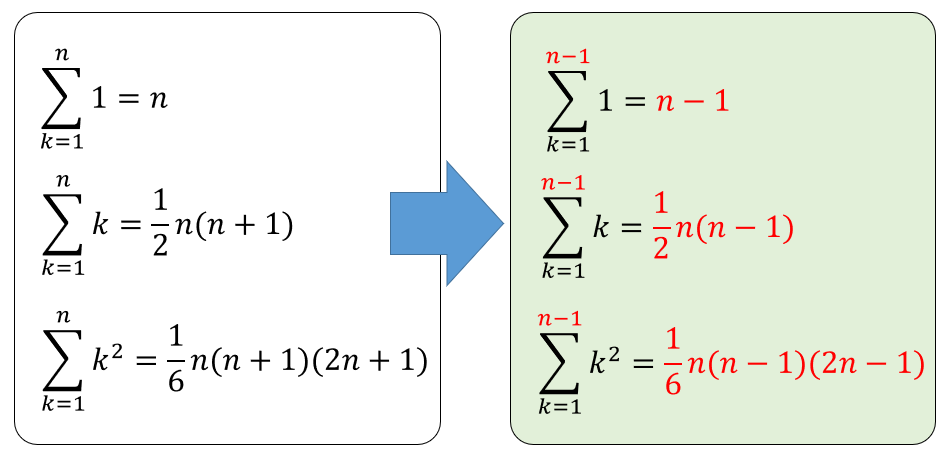
今後もよく使うので、\((n-1)\) の場合の形も覚えておくと便利です。
形も似ているから覚えやすいよね(^^)
では、Σの注意事項を確認したところで
先ほどの計算を続けていきましょう。
$$\begin{eqnarray}a_n&=&2+2\displaystyle \sum_{ k = 1 }^{ n-1 }k+\displaystyle \sum_{ k = 1 }^{ n-1 }1\\[5pt]&=&2+2\cdot \frac{1}{2}n(n-1)+(n-1)\\[5pt]&=&2+n^2-n+n-1\\[5pt]&=&n^2+1\end{eqnarray}$$
となりました。
よっしゃ!終わり!
としたくなるところですが、何度も何度も言うように…
こちらの公式で求めた一般項は、\(n≧2\) のときに限ります。
じゃぁ、\(n=1\) のときはどーすんの?
ってことで、最後にちょっとしたひと手間が必要になります。
先ほど求めた、\(n^2+1\) に\(n=1\) を代入して、
そのときの値が\(a_1\) の数と一致するかを確かめるのです。
では、確かめていきましょう。
\(n=1\)のとき、\(1^2+1=2\) となり\(a_1\) と一致していますね。
よって、先ほど求めた\(a_n=n^2+1\) は\(n≧2\) だけでなく、
\(n=1\) のときでも成り立つことが確認できたので、
すべての\(n\) において、一般項は\(a_n=n^2+1\) と表せる。
完!
となるわけです。
最後がちょっとだけめんどうですが(^^;)
必ず\(n=1\) と一致するかどうかの確かめをするようにしてください。
たまーに、\(a_1\) と一致しないような問題もあります。
(かなりイジワルな問題ですが…)
その場合には、仕方がないので次のような感じで一般項を表して答えとします。
【\(a_1\)が一致しない場合の一般項表し方の例】
$$\begin{eqnarray} a_n= \begin{cases} □n+〇 & ( n≧2 ) \\ △ & ( n=1 ) \end{cases} \end{eqnarray}$$
\(\{a_n\}\)の階差数列を\(\{b_n\}\) とすると、
\(b_n=2n+1\) と表せる。
\(n≧2\) のとき
$$\begin{eqnarray}a_n&=&a_1+\displaystyle \sum_{ k = 1 }^{ n-1 } b_k\\[5pt]&=&2+\displaystyle \sum_{ k = 1 }^{ n-1 }(2k+1)\\[5pt]&=&2+2\displaystyle \sum_{ k = 1 }^{ n-1 }k+\displaystyle \sum_{ k = 1 }^{ n-1 }1\\[5pt]&=&2+2\cdot \frac{1}{2}n(n-1)+(n-1)\\[5pt]&=&2+n^2-n+n-1\\[5pt]&=&n^2+1\end{eqnarray}$$
\(n=1\) のとき、\(1^2+1=2\) となり、\(a_1\) と一致するので \(n=1\) のときも成り立つ。
よって、求める数列の一般項は、\(a_n=n^2+1\cdots(解)\)
階差数列の和が等比になった場合には?
それでは、階差数列の問題を極めるため
こちらの問題に挑戦してみましょう!
次の数列の一般項を求めよ。
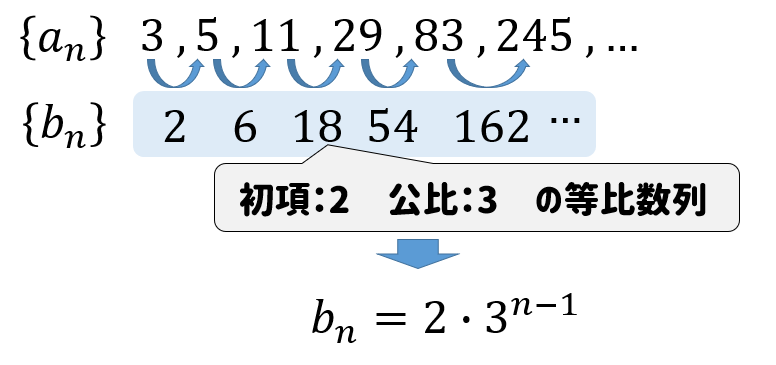
$$3, 5, 11, 29, 83, 245, \cdots$$
こちらも階差数列を使った問題となります。
今回は階差数列が、等比数列となっております。
この場合には、どのようにやっていくのでしょうか。
確認していきましょう!
まずは、階差数列の一般項を求める。
次に、公式に当てはめていく。
\(n≧2\) のとき
$$\begin{eqnarray}a_n&=&a_1+\displaystyle \sum_{ k = 1 }^{ n-1 } b_k\\[5pt]&=&3+\displaystyle \sum_{ k = 1 }^{ n-1 }(2\cdot3^{k-1})\end{eqnarray}$$
さて、ここで計算の手が止まってしまう人が多いのですが、
Σの計算は大丈夫でしょうか??
ここは等比数列の和の公式に当てはめて計算を進めていきます。
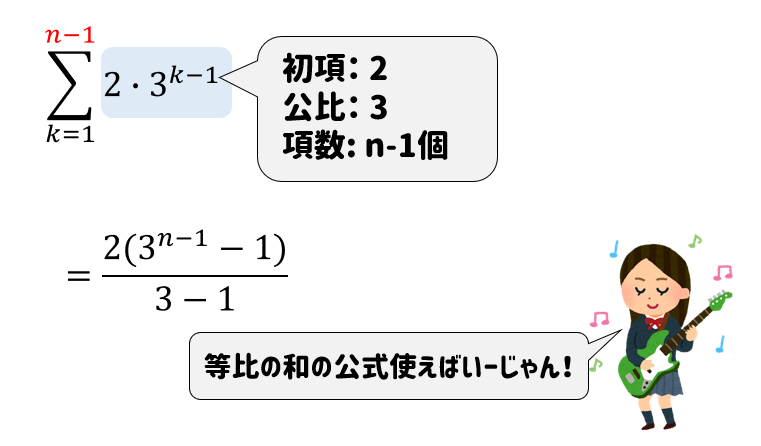
$$\begin{eqnarray}a_n&=&3+\displaystyle \sum_{ k = 1 }^{ n-1 }(2\cdot3^{k-1})\\[5pt]&=&3+\frac{2(3^{n-1}-1)}{3-1}\\[5pt]&=&3^{n-1}+2\end{eqnarray}$$
\(n=1\) のとき、\(3^{1-1}+2=3\) となり、\(a_1\)と一致するので\(n=1\) のときも成り立つ。
よって、求める数列の一般項は、\(a_n=3^{n-1}+2\cdots(解)\)
階差数列が等比数列になっている場合でも
基本的にはやり方同じ!
Σの計算方法がちょっと違ってくるだけだね。
漸化式と階差数列の問題
では、次に漸化式と階差数列が組み合わさった問題に挑戦してみましょう。
まぁ、簡単なのでサクッとね(/・ω・)/
次の条件で定められる数列\(\{a_n\}\) の一般項を求めなさい。
\(a_1=1\)、\(a_{n+1}-a_{n}=n\)
漸化式が次のような形で表されるときには、
階差数列を使って一般項を求めていきましょう。
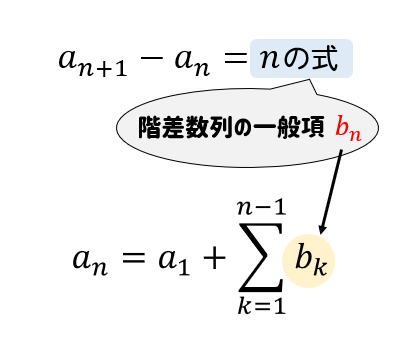
\(\{a_n\}\)の階差数列を\(\{b_n\}\) とすると、
\(b_n=n\) と表せる。
\(n≧2\) のとき
$$\begin{eqnarray}a_n&=&a_1+\displaystyle \sum_{ k = 1 }^{ n-1 } b_k\\[5pt]&=&1+\displaystyle \sum_{ k = 1 }^{ n-1 }k\\[5pt]&=&1+\frac{1}{2}n(n-1)\\[5pt]&=&\frac{2}{2}+\frac{1}{2}n(n-1)\\[5pt]&=&\frac{1}{2}\{2+n(n-1)\}\\[5pt]&=&\frac{1}{2}(n^2-n+2)\end{eqnarray}$$
\(n=1\) のとき、\(\frac{1}{2}(1^2-1+2)=1\) となり、\(a_1\) と一致するので \(n=1\) のときも成り立つ。
よって、求める数列の一般項は、\(a_n=\frac{1}{2}(n^2-n+2)\cdots(解)\)
【応用】階差数列を2回使う場合もある!
では、最後に階差数列を2回使う問題についても触れておきましょう。
こちらは手間が多いだけで、特別な知識を使うものではありません。
なので、サラッと解答を載せておきますので、
あ、こんなやり方もあるんだ…ということで頭に入れておいてもらえればと思います(^^)
次の数列の一般項を求めなさい。
$$1, 2, 5, 12, 25, 46, 77, 120, \cdots$$

まとめ!
お疲れ様でした!
階差数列を使った問題についてまとめてきましたが…
まぁ、計算がメンドイw
考え方はシンプルなものが多いのですが
計算が多いので、途中でミスが起こりやすい。
なので、階差数列の問題で点が取れるようになるためには
問題を解きまくって慣れるべし
というわけで、学校のテキストなどを使ってたくさん練習しておきましょう!











コメントを残す