【入試問題】(一部抜粋)
原点Oを通り四角形\(ACDB\)の面積を二等分する直線の式を求めなさい。
これはちょっと難しい問題です(^^;)
分かりにくいところは動画の解説を入れているので
最後まで頑張っていきましょう!
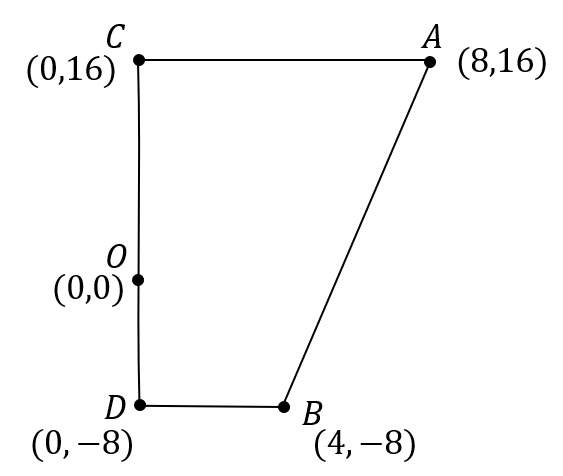
まずは、四角形\(ACDB\)の面積を考える必要があります。
台形の面積は、\((上底+下底)\times 高さ\times \frac{1}{2}\) でしたね。
それぞれの座標から長さを求めて、面積を出しましょう。
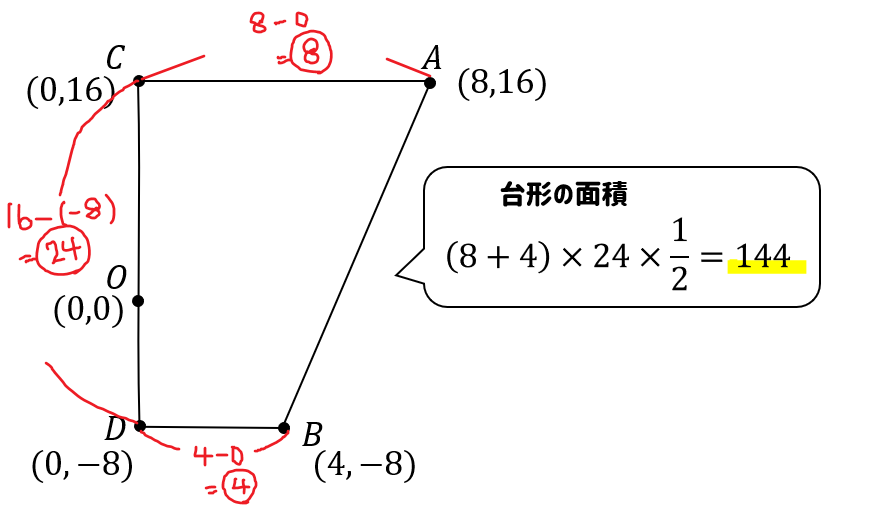
グラフ上の長さを求めるときには
(大きい座標)ー(小さい座標)
がポイントでしたね。
次に、点Oを通り四角形を二等分する直線を
イメージでよいので書き込んでみましょう。
するとこんな感じ。四角形と交わるところを点\(E\)としておきますね。
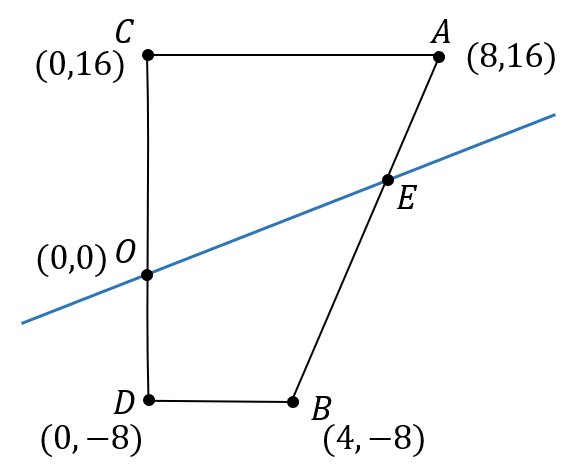
つまり、直線\(OE\)の式を作ればよいのですが
点\(E\)の座標が分かりません。
なので、点\(E\)がどういった場所にあるのかを探っていきましょう。
この直線は四角形の面積を二等分しているのだから
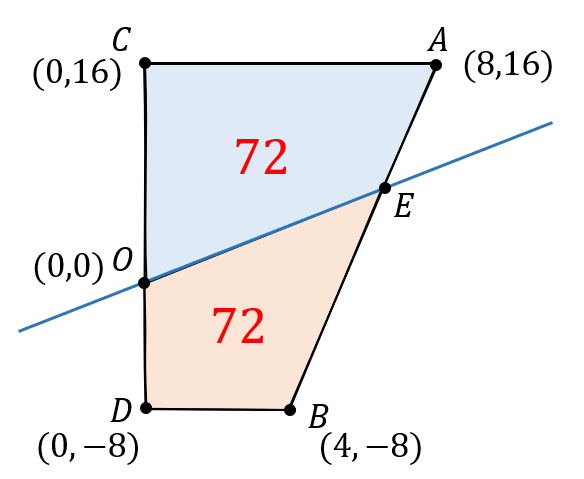
このように面積は\(144\)の半分である\(72\)ずつに分かれます。
2つにわかれた四角形のうち、上にある青い四角形に注目してみましょう。
すると、このように\(△OAE\)の部分は面積が\(8\)であることがわかります。
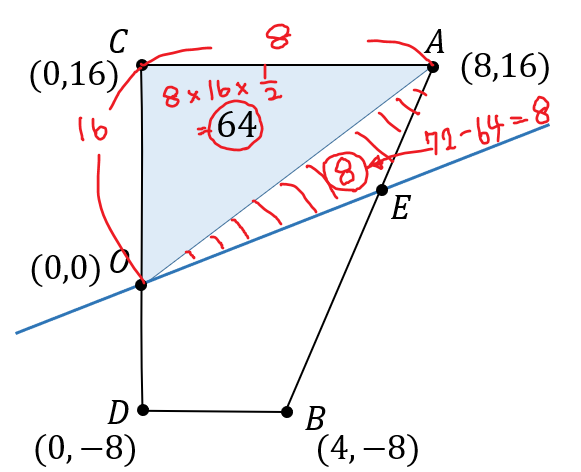
\(△OAC\)の面積をもとめて、全体の面積\(72\)から引くことで、\(△OAE\)の面積\(8\)を求めています。
同じように、今度は下にある赤い四角形に注目すると
このように\(△OBE\)の部分は面積が\(56\)であることがわかります。
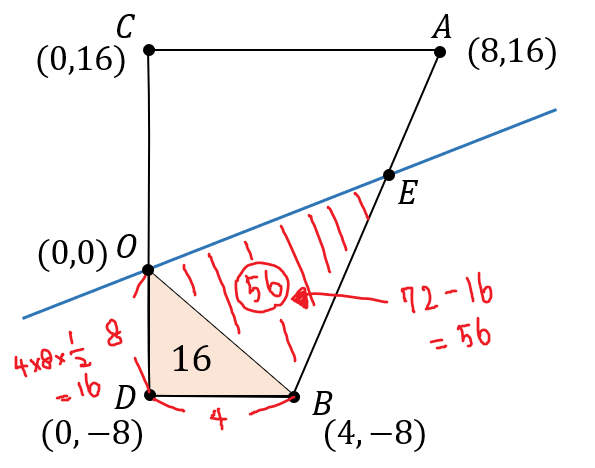
すると!
\(△OAE\)と\(△OBE\)の面積比が、\(8:56=1:7\)となることから
それぞれの三角形の底辺にあたる\(AE\)と\(EB\)の比も同じく\(1:7\)となります。
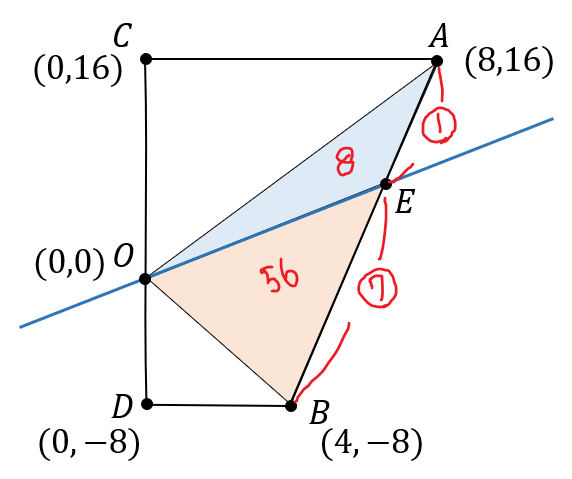
ここでは相似な図形の単元でよく利用した次の性質を用いています。

\(AE:EB=1:7\)であることが分かったら
次のような三角形を作って、平行線と線分の比を考えてみましょう。
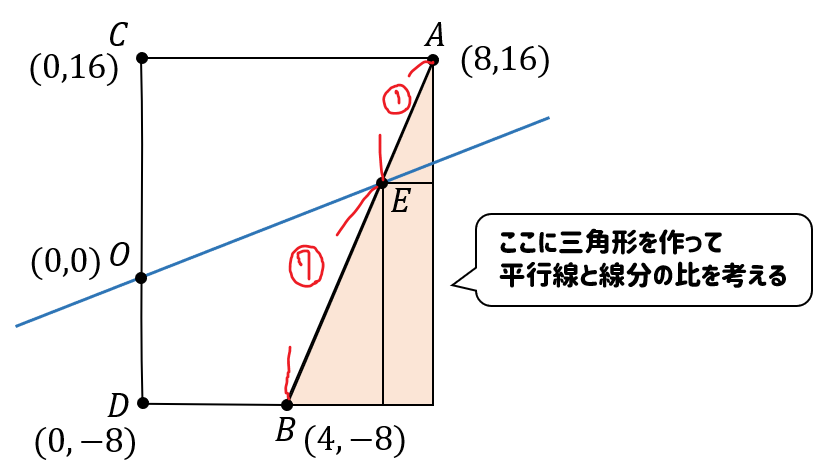
三角形の部分を取り出してみると
こんな感じでそれぞれ比を取ることができます。
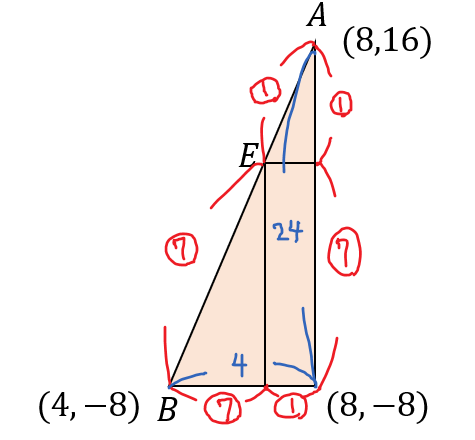
このことから次のように辺の長さを求めることができます。
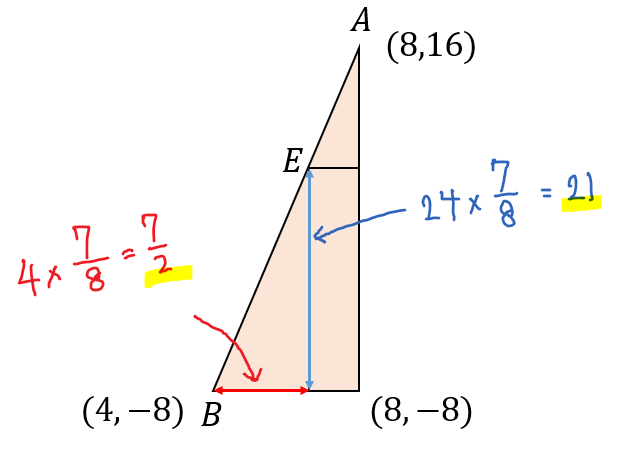
長さ4を8個に分けた7個分だから、\(4\times \frac{7}{8}=\frac{7}{2}\)
長さ24を8個に分けた7個分だから、\(24\times \frac{7}{8}=21\)
それぞれこのように計算します。
そして、点\(B\)から点\(E\)までの長さが求まったことから
いよいよ点\(E\)の座標が求まります。
点\(E\)が点\(B\)から横に\(\frac{7}{2}\)、縦に\(21\)の場所にあるので
\(x\)座標は、\(4+\frac{7}{2}=\frac{15}{2}\)
\(y\)座標は、\(-8+21=13\)
よって、点\(E(\frac{15}{2},13)\)となります。
ここの過程は複雑なので解説動画を用意しました。
点\(E\)の座標が求まれば、直線\(OE\)の式は簡単ですね!
原点を通る直線の式ですから、比例の式 \(y=ax\)に\((\frac{15}{2},13)\)を代入すればよいです。
$$\begin{eqnarray}13&=&a\times \frac{15}{2}\\[5pt]26&=&15a\\[5pt]a&=&\frac{26}{15} \end{eqnarray}$$
以上より
$$y=\frac{26}{15}x\cdots(解)$$
答え
$$y=\frac{26}{15}x$$
これはかなり難しい問題だったね(^^;)
式変形や解き方などで分からないところがあれば
コメント欄にてお知らせくださいませ(/・ω・)/

















コメントを残す