【二次方程式】平方根の考えを使った解き方、平方完成を利用した解き方を解説！

今回は、中3で学習する二次方程式の単元から

平方根の考え方を利用して計算する方法

について解説していくよ！

 

 

二次方程式の解き方は、大きく分けて4パターンあります。

 

 

この中から

平方根の考えを利用する解き方

平方完成を利用する解き方を具体例を交えながら解説していきます。

 

今回の記事を通して、以下のような問題が解けるようになります。

 

今回の記事はこちらの動画でも解説しています(/・ω・)/

 

平方根の考えを利用して方程式を解く

2乗すると\(a\)になる数を\(a\)の平方根といいましたね。

例えば

といった感じで、二乗してその数になるものを平方根といいます。

 

実は、この考え方を利用して、二次方程式を解くことができます。

\(x^2=5\)という二次方程式を詳しく見ていきましょう。

 

この方程式から読み取れることは

ということが読み取れます。

よって、\(x\)は５の平方根なので

$$x=\pm 5$$

というように、平方根の知識を利用して二次方程式を解くことができます。

 

 

この考え方に慣れてくると

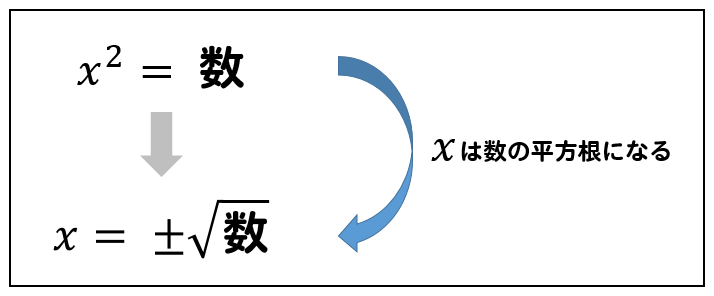
このように式変形をすることで、計算していくことができます。

 

二次方程式が、\(x^2=数\)の形になっていれば

２乗をなくして、数に±√をつける。

と覚えておきましょう。

 

 

 

これらの考え方を利用すると

\((x+6)^2=12\)も同様に解くことができます。

よって、\(x+6\)は12の平方根なので\(\pm \sqrt{12}\)であることがわかります。

 

$$x+6=\pm \sqrt{12}$$

ここから式変形をしながら\(x\)の値を求めると

$$x+6=\pm 2\sqrt{3}$$

$$x=-6 \pm 2\sqrt{3}$$

となります。

 

 

このように、２乗になっている部分が\(x\)の式になっていても平方根の考え方を利用して解くことができますね。

 

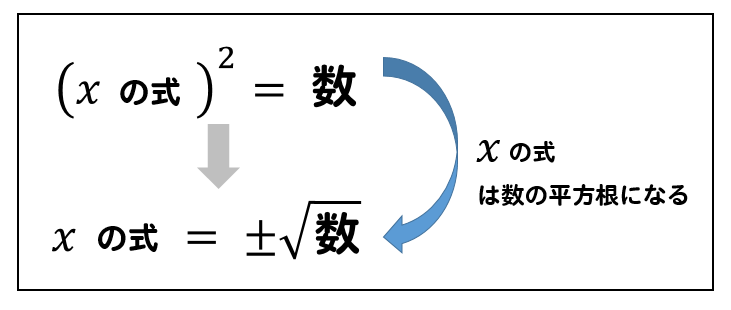
こちらも

２乗をなくして数に±√をつける。

と覚えておきましょう。

 

 

それでは、これらの解き方をマスターするために練習問題に挑戦してみましょう。

 

練習問題を通して理解を深めよう！

 

（1）解説＆解答　移項してしまえ！

 

\(x^2=数\)の形にするために

16を右辺に移項してやります。

$$x^2=16$$

この形が作れたら、平方根の考え方を使って

$$x=\pm 4$$

となります。

 

（2）解説＆解答　係数は割ってしまえ！

 

\(x^2\)に邪魔な係数３がついていますね。

こういうときは、両辺を３で割ってしまいましょう。

$$3x^2 \div 3=21\div 3$$

$$x^2=7$$

これで、平方根の考え方を利用できる形ができたので

$$x=\pm \sqrt{7}$$

となります。

 

（3）解説＆解答　分数の方でも平方根の考え方を！

 

（2）と同様、\(x^2\)に邪魔な係数９がついているので

まずは両辺を９で割ってやりましょう。

$$9x^2 \div 9=7 \div 9$$

$$x^2=\frac{7}{9}$$

ここから平方根の考え方を利用して解いていきます。

$$x=\pm \sqrt{\frac{7}{9}}$$

$$x=\pm \frac{\sqrt{7}}{3}$$

 

（4）解説＆解答　式でも平方根の考え方を！

 

\(x-3\)が27の平方根になるという考え方を利用して解いていきましょう。

$$x-3=\pm \sqrt{27}$$

$$x-3=\pm 3\sqrt{3}$$

$$x=3 \pm 3\sqrt{3}$$

 

（5）解説＆解答　計算は最後まで！

 

\(x-1\)が9の平方根になるという考え方を利用して解いていきましょう。

$$x-1=\pm 3$$

$$x=1 \pm 3$$

 

ここで終わりにしないでください。

\(1\pm 3\)というのは

\(1+3\)と\(1-3\)をまとめて表した形になります。

 

それぞれ、まだ計算ができるので

答えは\(x=4,-2\)というように

最後まで計算をしてやってください。

 

(4)の答え

\(3+3\sqrt{3}\)と\(3-3\sqrt{3}\)はこれ以上計算できないので

\(3\pm 3\sqrt{3}\)と表した状態で答えとします。

 

平方の形を作る平方完成を利用した解き方

\(x^2=数\)や\((xの式)^2=数\)

といった形であれば平方根の考えを利用して解くことができました。

 

だけど

$$x^2+10x-16=0$$

というような方程式の場合

 

あれ…平方根の形になっていないから解けないじゃん

と、困ってしまいますよね。

 

 

 

それならば！ということで

方程式を変形して、平方根の考え方が利用できる形を無理やり作ってしまいましょう。

 

これを

平方完成

と言います。

 

それでは、\(x^2+10x-16=0\)の形を平方完成していきます。

 

まずは\(-16\)を右辺に移項して

左辺を\(x\)だけ、右辺を数だけにします。

 

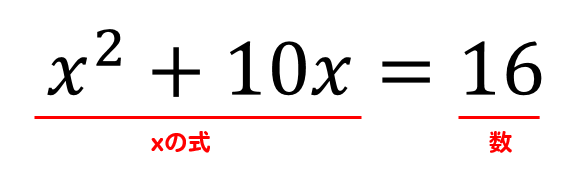
次に\(x\)の係数である10に注目して

10の半分である5を2乗した数を両辺に加えます。

 

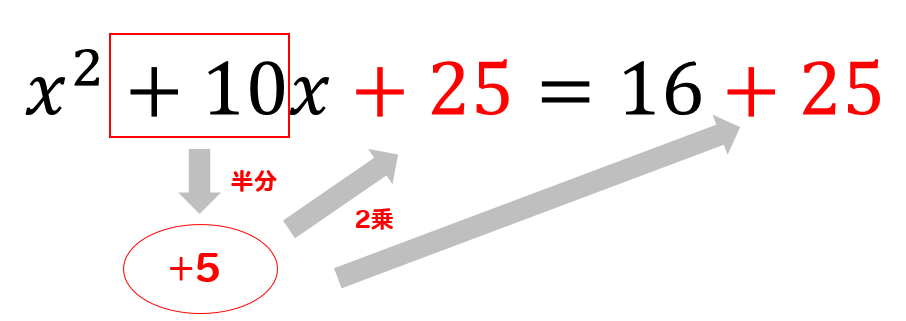
この作業をすることで

左辺が因数分解できるようになります。

よって、このように

平方根の考え方が利用できる形に変形することができました。

この一連の変形をまとめて、平方完成といいます。

 

 

 

係数を半分にして2乗

という作業はちゃんと覚えておかないとミスしやすいところです。

何回も練習を重ねて、手順を身につけておきましょう。

 

それでは、練習問題を通して

平方完成の理解を深めていこう！

 

平方完成のやり方についてはこちらの動画でも解説しています。

練習問題を通して理解を深めよう！

 

（1）解説＆解答

 

まずは３を右辺に移項して、\(x\)の式と数を分けます。

$$x^2-8x=-3$$

次に\(x\)の係数である-8に注目して

-8の半分である-4を2乗した数16を両辺に加えます。

$$x^2-8x+16=-3+16$$

左辺を因数分解すると

$$(x-4)^2=13$$

$$x-4=\pm \sqrt{13}$$

$$x=4\pm \sqrt{13}$$

 

（2）解説＆解答

 

まずは３を右辺に移項して、\(x\)の式と数を分けます。

$$x^2+5x=-3$$

次に\(x\)の係数である5に注目して

5の半分である\(\displaystyle \frac{5}{2}\)を2乗した数\(\displaystyle \frac{25}{4}\)を両辺に加えます。

$$x^2+5x+\frac{25}{4}=-3+\frac{25}{4}$$

左辺を因数分解すると

$$(x+\frac{5}{2})^2=\frac{13}{4}$$

$$x+\frac{5}{2}=\pm \frac{\sqrt{13}}{2}$$

$$x=-\frac{5}{2} \pm \frac{\sqrt{13}}{2}$$

 

【追加演習プリント】自宅学習で伸ばしたい方へ！

この記事を読んでくださっている保護者さんの方へ！

ここで紹介してる例題を一通り理解してもらえれば、平方根を利用した解き方はバッチリです＾＾

あとは実戦演習を通して、手本がなくてもスラスラと解けるようにしておいてもらいたいです！

 

というわけで、自宅学習で活用してもらいたい演習プリントを用意しました。

ここで取り上げている問題はこちら！

問題＆解説をプリント形式で用意しているので、こちらを印刷してお子さんに渡してあげてください＾＾

10分ほどで取り組める分量になっているので、スキマ時間を活用して二次方程式の理解度を高めておきましょう！

勉強のスタート時に小テストとして取り組んでみると、イイ感じに集中力が高まって、その日の学習がスムーズになってくるかもしれませんね(‘ω’)ノ

 

追加演習をやってテストの点数をUPさせたい方には、課題プリントをメールで送らせてもらっています。

 

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

 

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

まとめ

お疲れ様でした！

二次方程式にはいろんな解き方があるのですが

そのうちの１つ

平方根の考えを利用した解き方についてでした。

 

他の解き方についても、他記事を通して紹介していくので

すべての解き方をしっかりと理解していきましょう！

 

二次方程式の解き方4パターンについてはこちらをどうぞ！

• 平方根の考えを利用して解く　⇐ 今回の記事
• 因数分解を利用して解く
• 解の公式を利用して解く
• 平方完成を利用して解く