あれ?
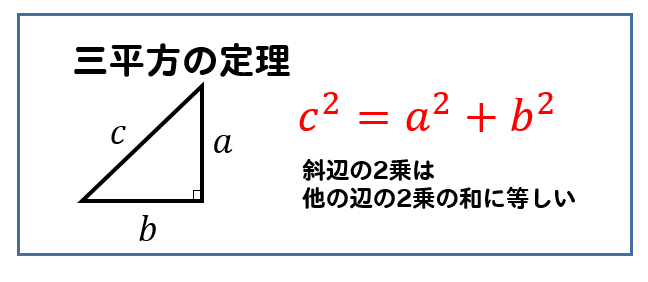
三平方の定理ってさ
直角三角形のときに使える定理だったよね

斜辺の長さを2乗は、他の辺の2乗の和に等しい。
これって
鋭角三角形や鈍角三角形の場合にはどうなるんだろう?

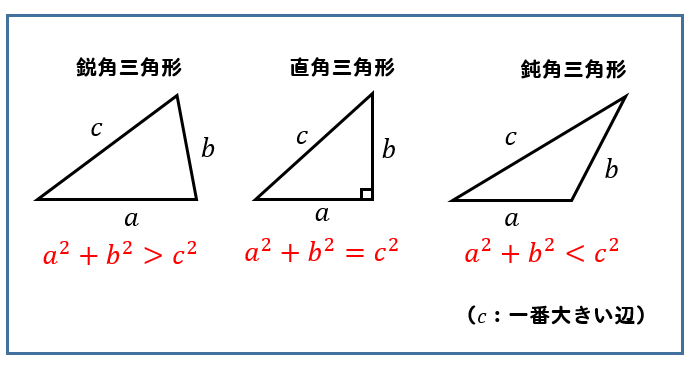
鋭角、直角、鈍角三角形における辺の長さの関係
というわけで
鋭角、直角、鈍角
それぞれのときに辺の長さにはどのような特徴があるかをまとめておきます。

直角三角形の場合
斜辺の長さの二乗が他の辺の二乗の和に等しいでしたが

鋭角三角形の場合
一番大きい辺の長さの二乗は他の辺の二乗の和より小さい

鈍角三角形の場合
一番大きい辺の長さの二乗は他の辺の上の和より大きい

という特徴があります。
そして
これは逆も成り立ちます。
逆の性質を利用すれば、次のように三角形の形を見分けることができます。
三角形の見分け方
△ABCにおいて辺の長さを小さい順に\(a,b,c\)とすると
\(a^2+b^2>c^2\) ならば △ABCは鋭角三角形
\(a^2+b^2=c^2\) ならば △ABCは直角三角形
\(a^2+b^2<c^2\) ならば △ABCは鈍角三角形
この特徴を覚えておけば
次のような問題を解くことができるようになります。
三角形の見分け問題に挑戦!
3辺が次のような三角形のとき
鋭角、直角、鈍角三角形のどれになるかを答えなさい。
$$(1) 6cm, 8cm, 10cm$$
$$(2) 3cm, 4cm, 6cm$$
$$(3) 2cm, 3cm, \sqrt{5}cm$$
$$(4) \sqrt{3}cm, \sqrt{5}cm, 2cm$$
(1)答えはこちら
(1)答え
\(6^2+8^2=10^2\)より、直角三角形
一番大きい長さを2乗すると
$$10^2=100$$
そして、他の辺の2乗の和を計算すると
$$6^2+8^2=36+64=100$$
それぞれの値が等しくなったので
$$6^2+8^2=10^2$$
となります。
よって、直角三角形になるということがわかります。
(2)答えはこちら
(2)答え
\(3^2+4^2<6^2\)より、鈍角三角形
一番大きい長さを2乗すると
$$6^2=36$$
そして、他の辺の2乗の和を計算すると
$$3^2+4^2=9+16=25$$
それぞれの値は\(25<36\)となり
$$3^2+4^2<6^2$$
となるので
鈍角三角形になるということがわかります。
(3)答えはこちら
(3)答え
\(2^2+(\sqrt{5})^2=3^2\)より、直角三角形
まずは一番大きい長さを2乗したいのですが
\(2cm,3cm,\sqrt{5}cm\) どれが一番大きいのか判断しにくいです…
$$\sqrt{5}=2.236 \cdots$$
ということを覚えておけば、すぐに分かります。
覚えてないよ…( ;∀;)
という方は、これらの辺を全て2乗して比較してやると
$$2cm \rightarrow 4 小$$
$$3cm \rightarrow 9 大$$
$$\sqrt{5}cm \rightarrow 5 中$$
$$2<\sqrt{5}<3$$
ということがわかります。
よって、一番長い長さの2乗は
$$3^2=9$$
そして、他の辺の2乗の和を計算すると
$$2^2+(\sqrt{5})^2=4+5=9$$
それぞれの値は等しいので
$$2^2+(\sqrt{5})^2<3^2$$
となります。
よって、直角三角形になるということがわかります。
(4)答えはこちら
(4)答え
\(2^2+(\sqrt{3})^2>(\sqrt{5})^2\)より、鋭角三角形
まずは一番大きい長さを2乗したいのですが
どれが一番大きいのか判断しにくいです…
さっきは2乗をして比較する方法を紹介しましたが
今回はすべてを√の形に変換して比較する方法をやってみましょう。
$$2cm = \sqrt{4}cm$$
なので
$$\sqrt{3}<\sqrt{4}<\sqrt{5}$$
となるので
$$\sqrt{3}<2<\sqrt{5}$$
よって、一番大きい長さは\(\sqrt{5}cm\)だとわかります。
一番長い長さの2乗は
$$(\sqrt{5})^2=5$$
そして、他の辺の2乗の和を計算すると
$$2^2+(\sqrt{3})^2=4+3=7$$
それぞれの値は\(7>5\)という関係より
$$2^2+(\sqrt{3})^2>(\sqrt{5})^2$$
となります。
よって、鋭角三角形になるということがわかります。
まとめ
三平方の定理とは
直角三角形のときに利用できる
辺の長さの関係式でしたね。
それを発展させて考えていくと
直角三角形だけでなく
鋭角、鈍角三角形を見分ける方法として活用することができます。
入試などでは、活用する機会は少ないと思いますが
図形問題を解いていく上で知っておくと便利な知識でもあります。
△ABCにおいて、AB=3㎝、BC=4㎝、CD=6㎝とする…
と問題に出てきたら
イメージ図を書きながら問題を解くと思います。
このときに今回の知識を持っていたら
あ!この長さの関係だと鋭角三角形になる!
と、わかるので正確な図形を書いていくことができます。
正確な図形を書くことは、正解を導くためのヒントになるからね
とっても大切なことです(^^)
だから、ちゃんと覚えておこうねー!
ファイトだー(/・ω・)/

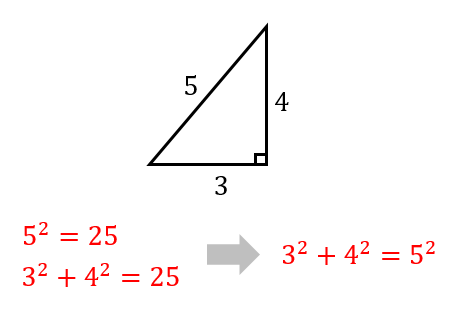
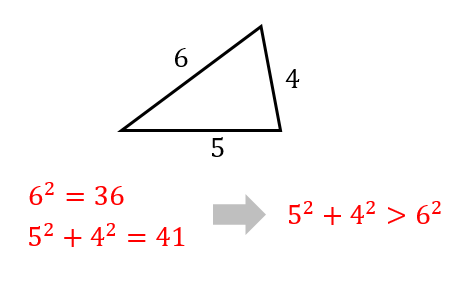
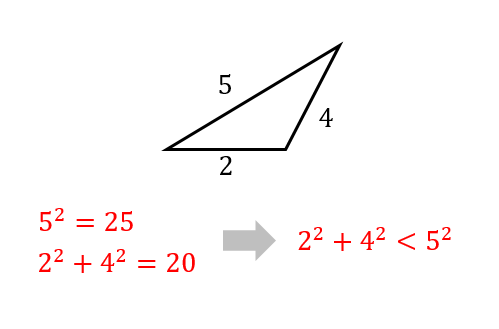


















コメントを残す