今回は連立方程式の入試問題に挑戦の第2回!
速さに関する文章問題に取り組んでいきましょう。
問題
Aさんの自宅からバス停までと、バス停から駅までの道のりの合計は3600mである。ある日、Aさんは自宅からバス停まで歩き、バス停で5分間待ってから、バスに乗って駅に向かったところ、駅に到着したのは自宅を出発してから、20分後であった。Aさんの歩く速さは毎分80m、バスの速さは毎分480mでそれぞれ一定とする。
このとき、Aさんの自宅からバス停までの道のりを\(x\)m、バス停から駅までの道のりを\(y\)mとして連立方程式をつくり、自宅からバス停までとバス停から駅までの道のりをそれぞれ求めなさい。
んー
文章が長い!
文を長くして、難しく見せてくるあたり入試問題の特徴と言えますね。
1つ1つ丁寧に読み解いていきましょう。
問題の考え方!
まず、自宅、バス停と駅の関係を明確にしておきましょう。
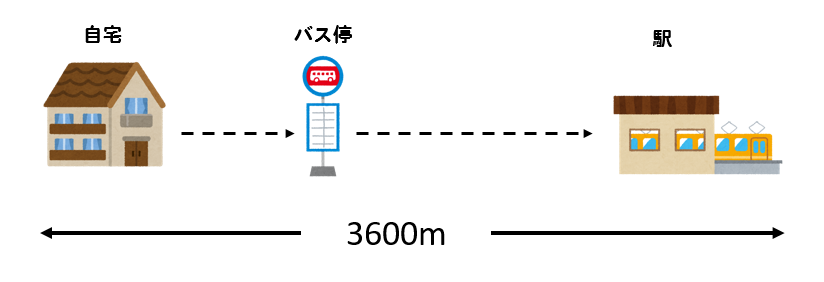
こんな感じですね。
自宅と駅の間にバス停があって
距離は3600mあるよってこと。
自宅からバス停までの道のりを\(x\)m
バス停から駅までの道のりを\(y\)mとすることから
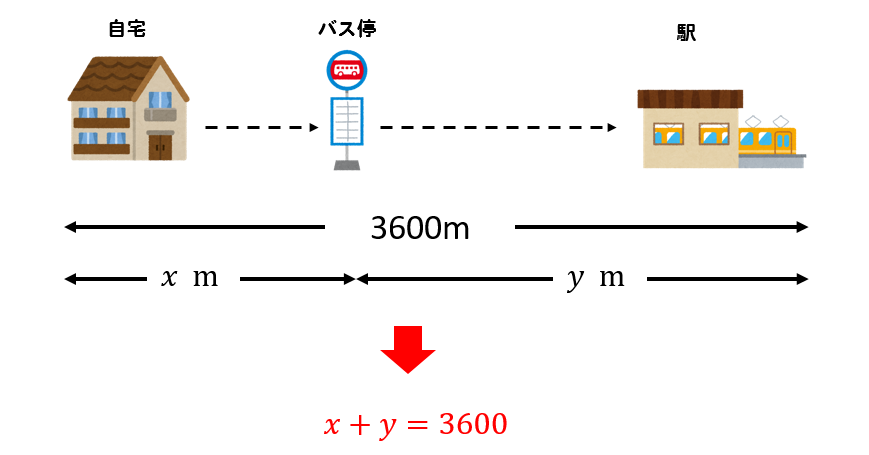
道のりの情報から
$$x+y=3600$$
という式が作れました。
次に時間に関する情報を読み解いていきましょう。
時間を考えるときには、”みはじ”の計算が役に立ちます。
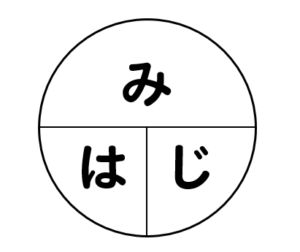
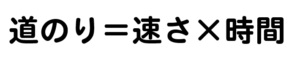


速さの計算方法を忘れてしまった人は、こちらの記事で復習しておきましょう!
それでは、自宅からバス停、バス停から駅までにかかった時間を求めると
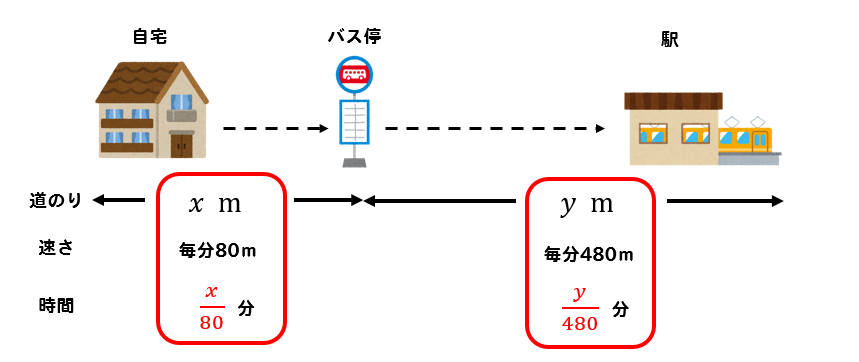
このようになります。
自宅からバス停までは
道のり\(x\)、速さが80なので
$$(時間)=x\div 80=\frac{x}{80}$$
バス停から駅までは
道のり\(y\)、速さが480なので
$$(時間)=y\div 480=\frac{y}{480}$$
となります。
自宅から駅まで合計で20分かかったこと
途中のバス停で5分待っていたことを考えると
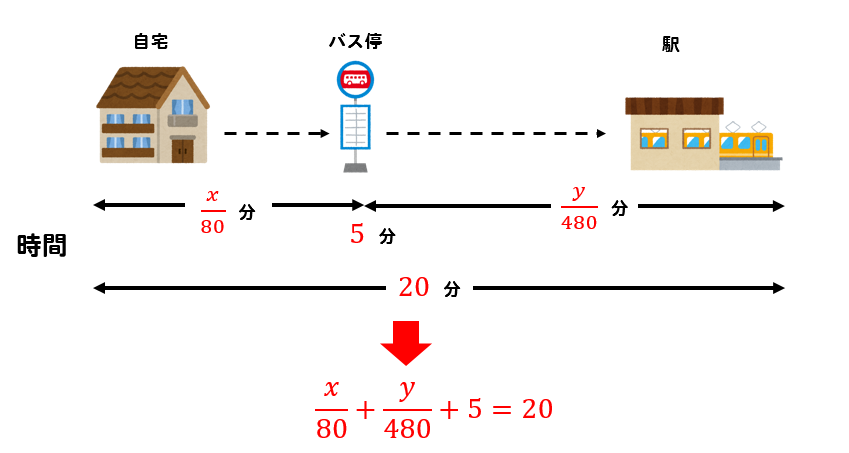
$$\frac{x}{80}+\frac{y}{480}+5=20$$
という式が作れました。
以上より
2本の式が作れたので
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}x+y=3600 \\\frac{x}{80}+\frac{y}{480}+5=20 \end{array} \right. \end{eqnarray}}$$
このような連立方程式を解いていけば、答えを出すことができます(^^)
問題の答えと解説!
Aさんの自宅からバス停までと、バス停から駅までの道のりの合計は3600mである。ある日、Aさんは自宅からバス停まで歩き、バス停で5分間待ってから、バスに乗って駅に向かったところ、駅に到着したのは自宅を出発してから、20分後であった。Aさんの歩く速さは毎分80m、バスの速さは毎分480mでそれぞれ一定とする。
このとき、Aさんの自宅からバス停までの道のりを\(x\)m、バス停から駅までの道のりを\(y\)mとして連立方程式をつくり、自宅からバス停までとバス停から駅までの道のりをそれぞれ求めなさい。
上で解説した通り
道のりと時間に注目して、それぞれ式を作ります。
すると次のような方程式が作れるので
あとはこれを解いていくだけですね!
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}x+y=3600 \\\frac{x}{80}+\frac{y}{480}+5=20 \end{array} \right. \end{eqnarray}}$$
$$\frac{x}{80}+\frac{y}{480}+5=20$$
この式は、このままでは複雑なので分数を消して整理してからスタートしましょう。
まずは5を右辺に移項。
$$\frac{x}{80}+\frac{y}{480}=15$$
次に分母を消すため、両辺に480をかけます。
$$6x+y=7200$$
すると、ここまでシンプルな形に変形できました。
この式を使って連立方程式を解いていきましょう。

よって
自宅からバス停までの道のりは720m
バス停から駅までの道のりは2880mとなります。
答え
自宅からバス停までの道のりは720m
バス停から駅までの道のりは2880m
まとめ
お疲れ様でした!
速さの文章問題では、”みはじ”の計算ができるかどうかが大切なポイントとなります。
だけど、この計算ができてしまえば
式の作り方だったり
連立方程式の解き方だったりは
非常に基本的!って感じですね。
しっかりとマスターしておきましょう(^^)
速さに関する方程式の問題は
他にもこちらで解説しています。
【方程式利用】何分後に追いつくか?速さの文章問題を徹底解説!
【連立方程式】途中で速さが変わる文章問題の解き方、コツを解説!
参考にしてみてください(/・ω・)/



















良かったよ
良かったよ良いね
ありがとうございます^^