【入試問題】
\(2\sqrt{7}-3\)の小数の部分を\(a\)とするとき、\(a^2+5a\)の値を求めよ。
まずこちらの問題で確認しておきたいのが
$$(小数部分)=(全体)-(整数部分)$$
で求めることができるという点ですね。
小数部分\(a\)の値を求める必要がありますが
まずは整数部分がどうなるのかを考えていきます。
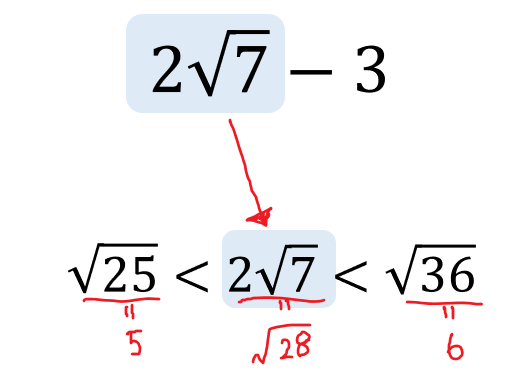
まずは、\(-3\)の部分は置いといて
\(2\sqrt{7}\)がどのような値になるのかを考えます。
このとき、ルートの外にある数は中に入れてから考えるようにしてください、
$$2\sqrt{7}=\sqrt{2^2\times 7}=\sqrt{28}$$
そして、この範囲に\(-3\)をすることによって
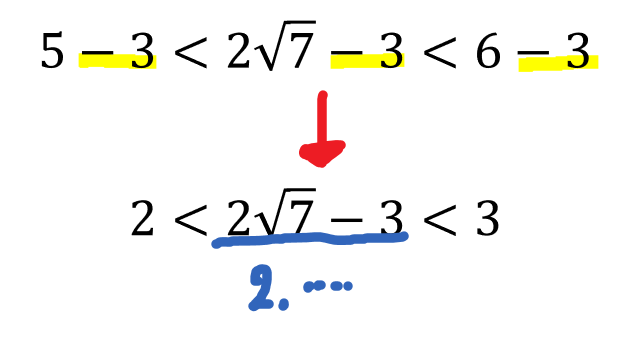
\(2\sqrt{7}-3\)の整数部分が\(2\)であることが分かりました。
整数部分が求まったので、次は小数部分を求めましょう。

小数部分が求まったら
あとは、\(a^2+5a\)に代入すれば完成となります。
が、ここでも1つ注意があります!!
そのまま代入すると計算が大変すぎるぞ…
なので、\(a^2+5a=a(a+5)\)と因数分解をしてから代入するようにしましょう。
入試レベルの問題であれば、式を工夫してから代入することが多いです。
$$\begin{eqnarray}a^2+5a&=&a(a+5)\\[5pt]&=&(2\sqrt{7}-5)\{(2\sqrt{7}-5)+5\}\\[5pt]&=&(2\sqrt{7}-5)\times 2\sqrt{7}\\[5pt]&=&28-10\sqrt{7}\cdots(解) \end{eqnarray}$$
答え
$$28-10\sqrt{7}$$
ちょっと難しい問題だったけど理解できたかな?
式変形や解き方などで分からないところがあれば
コメント欄にてお知らせくださいませ(/・ω・)/

















コメントを残す