今回は中2で学習する連立方程式の単元から
途中で速さが変わる文章問題について解説していくよ!
途中で速さが変わる問題とはこんなやつだね
問題
A町から9㎞はなれたB町へ行った。はじめは時速4㎞で歩き、途中から時速6㎞で走ったら全体で2時間かかった。歩いた道のり、走った道のりをそれぞれ求めなさい。
はじめは~、途中から~で…
というような途中で速さが変わるような文章問題です。
定期テストや入試でもよく見かける有名な問題ですね。
同時に苦手な人もすっごく多い問題です(^^;
今回は、この速さの問題を完全マスターしていきましょう!
今回の記事はこちらの動画でも解説しています(/・ω・)/
[スタセミ中2バナー]
速さの文章題を解くコツ!
この文章問題を解くためのコツがあります。
それは
みはじの表を作ること!
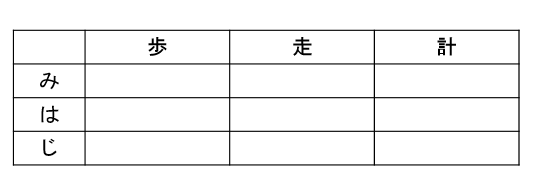
それでは、この表を使ってどのように解いていくのか解説していきます。
表を埋めていく
まず、歩いた道のりを\(x\)m、走った道のりを\(y\)mとします。
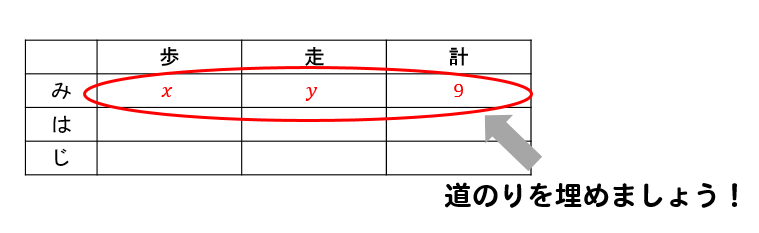
道のりの合計は、問題文の
『A町から9㎞はなれたB町へ行った。』
の部分から読み取れますね。
次は、速さの部分を埋めていきます。
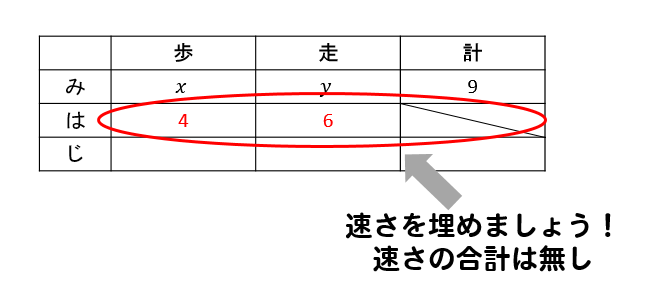
速さに合計という考えはないので、計の欄は×にしておきましょう。
最初に時速4㎞、途中から時速6㎞だからといって
合計は時速10㎞にはならないよね!
速さが合計できる世界なら楽ちんなのにねー
みはじを利用して時間を埋める
道のりと速さがそれぞれ埋まったら
みはじを利用して、時間を埋めていきます。
みはじを使った文字の表し方についてはこちらの記事をご参考ください。

時間はこのように求めることができるので
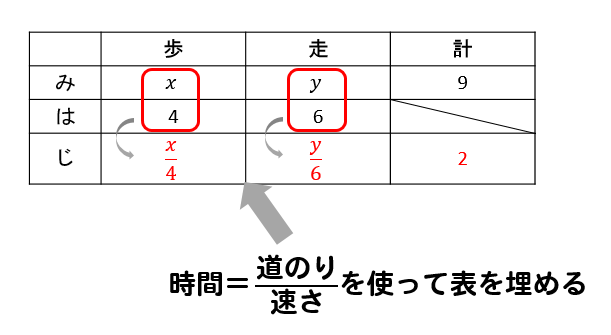
これで表が完成しました!
式を作る
表が完成したら
ここから連立方程式を作ります。
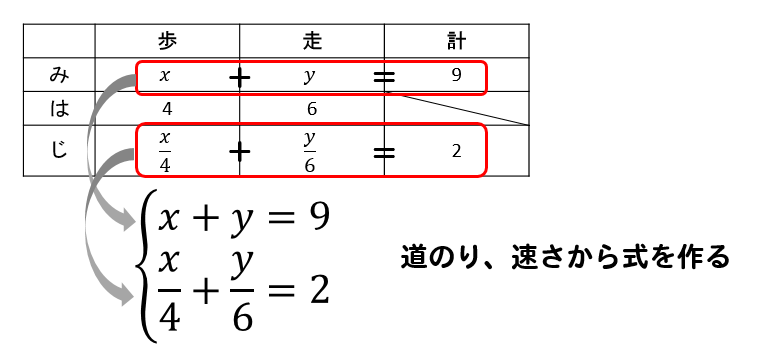
これで方程式が完成しました!
分数の方程式を計算!
方程式が完成したら
ここからは計算あるのみです。
速さの文章問題では、分数がつきものなので
分数の計算にも慣れておく必要がありますね。
分数のままだと計算が難しいので、分数を消す作業をしていきましょう。
分母にある4と6の最小公倍数である12を両辺にかけて
$$\frac{x}{4}\times 12+\frac{y}{6}\times 12=2\times 12$$
$$3x+2y=24$$
ここから連立方程式を計算していきましょう。
$$\begin{eqnarray} \left\{ \begin{array}{l} x + y = 9 \\ 3x + 2y = 24 \end{array} \right. \end{eqnarray}$$
係数を揃えで加減法で計算していきます。
$$\begin{eqnarray} \left\{ \begin{array}{l} 2x +2y = 18 \\ 3x + 2y = 24 \end{array} \right. \end{eqnarray}$$
$$-x=-6$$
$$x=6$$
\(x+y=9\)に\(x=6\)を代入すると
$$6+y=9$$
$$y=3$$
よって
歩いた道のりは6㎞、走った道のりは3㎞
ということが求められました!
表を作って、それぞれの値を埋めることができれば
あとは簡単に式を作って解くことができますね!
すこし面倒に思うかもしれませんが

この表を使えると、一気に楽になりますね(^^)

時間・道のりの単位を変換する問題
速さの文章問題にはちょっとした引っ掛け問題があります。
以下の問題を見て、どこの部分がポイントか分かりますか?
パターン①
問題
A町から16㎞はなれたB町へ行った。はじめは時速3㎞で歩き、途中から時速4㎞で走ったら全体で4時間30分かかった。歩いた道のり、走った道のりをそれぞれ求めなさい。
ここの部分ですね
『全体で4時間30分かかった。』
時間と分の両方でかいてあるので
どのように式を作ればいいかが分かりにくいですね。
このような場合には
速さの単位に揃えて、時間を変換していきます。
時速であれば、時間に変換
分速であれば、分に変換
秒速であれば、秒に変換
というように速さの単位を基準に、時間の単位を変換してください。
今回の問題であれば
速さは時速で表されているので
4時間30分を分を使わず、時間だけで表していきましょう。
4時間30分 ⇒ 270分 ⇒ \(\displaystyle \frac{270}{60}=\frac{9}{2}時間\)
このように時間を変換してから表を埋めていくようにしましょう。
時間の変換については、こうでしたね。

時間の変換が苦手な人は
練習問題を置いておくので挑戦してみてください。
(1)3時間20分を時間に変換しなさい。
(2)\(\displaystyle \frac{2}{3}\)を分に変換しなさい。
パターン②
問題
A町から1.2㎞はなれたB町へ行った。はじめは分速50mで歩き、途中から分速200mで走ったら全体で18分かかった。歩いた道のり、走った道のりをそれぞれ求めなさい。
今回の問題の引っかけポイントは
『A町から1.2㎞はなれたB町へ行った。』
の部分ですね。
今回の問題では速さが
分速〇mとなっていることから
時間は分を基準に。
道のりはmを基準に統一していかないといけません。
よって
1.2㎞ ⇒ 1200m
と変換してから表を埋めていくようにしましょう。
まとめ
お疲れ様でした!
途中で速さが変わる問題では
みはじの表を埋めていくことがコツでしたね。
また、単位の変換が必要な場合もあるので
問題文に出てくる速さの単位に注目して
道のり・時間の単位を変換していくことも忘れないようにしてくださいね!
たくさん練習して身につけていこうね
ファイトだー(/・ω・)/















すごくわかりやすかった。