こんにちは!数スタの小田です。
今回は方程式の利用(文章問題)の中でも速さに関する問題を取り上げていきます。
何分後に追いつくか?

という問題です。
速さの問題は苦手な人も多いと思うので丁寧にじっくりと解説していきますね!
では、解説いきましょー!
※ここでは、速さに関する文字式の表し方を用います。苦手な方はこちらの記事を先に読んでおいてもらえると理解しやすいかと思います。
今回の記事はこちらの動画でも解説しています(/・ω・)/


追いつく問題とは
何分後に追いつくか?というのは以下のような問題ですね
問題
弟が5㎞離れた公園に向かって家を出発した。弟の忘れ物に気付いた兄は、その8分後に家を出発して弟を追いかけた。弟の歩く速さは分速50m、兄の歩く速さは分速70mでした。このとき、兄は家を出発してから何分後に追いついたか求めなさい。また、追いついた地点は家から何mの地点か求めなさい。
うぉ…
文章が長い…
この時点で嫌になってしまいそうですが、何とか堪えてください。
言ってる内容はとてもシンプルなことなので。
何分後に追いつく?という問題を要約すると
誰かが出発


誰かが追いかける


そして、追いつく


追いついたタイムは?ここはどこ?


問題の流れはこういったものになります。
この問題で要求されていることは
- 誰かが追いかけ始めてから追いつくまでの時間は?
- 追いついた場所はどこ?
という2点です。
追いつく問題を解くためのポイントとは
こういった何分後に追いつくか?
という問題を解くためには必ず知っておきたいポイントがあります。
追われる人と追いかける人
追いついた場所においては
2人とも進んだ道のりが等しくなる
ということです。
イメージ湧くかな?
追いついたということは2人とも同じ場所にいるということですね。
そして、2人ともスタート地点は同じなので、出発時刻は違えど、進んできた距離は同じになるはずだよね。
つまり、考え方としては、2人の進んだ道のりをそれぞれ文字で表してイコールで結ぶことによって方程式を完成さていくことになります。
解き方の手順を考えよう
それでは、2人の道のりが等しくなるというポイント利用しながら解法手順を見ていきましょう。
手順① 追いつくまでの時間を文字で置く
兄は家を出発してから何分後に追いついたか求めなさい。
とあるので、兄が家を出発してから追いつくまでの時間をx分とします。
すると、兄と弟それぞれが進んでいた時間はこのようになります。
兄…x分
弟…(x+8)分
これもイメージが湧くかな?
兄は弟が出発してから8分後に追いかけ始めたんだよね
ということは、弟の方が兄よりも8分多く進んでいたってことになる。
だから、弟は兄よりも8多いってことで
(x+8)分と表すことができます。
もしも、弟が出発してから追いつかれるまでの時間をx分とした場合には、兄は弟よりも進んでいた時間が8分短いので、兄の方は(x-8)分と表すことができます。
何を基準として文字で置いたかによって表し方は変わってくるから、よーく考えてから文字で表すようにしようね。
手順② それぞれの道のりを文字で表す
それぞれの時間が表せたところで、次はそれぞれの道のりを表していきます。
ここで大事になるのが『み・は・じ』の関係性ですね。
「何それ??」
という方は、しつこいですがこちらの記事をご参考に。
道のりの表し方は
道のり=速さ×時間
でしたね。
というわけで、弟の道のりを求めていくと
速さが50、時間が(x+8)なので
道のりは50(x+8)と表せます。
兄の道のりも同様に
速さが70、時間がxなので
道のりは70xと表せます。
それぞれの道のりが求まれば最後の仕上げ!
手順③ 方程式を完成させて解く
お互いの道のりは等しくなるはずなので、それぞれの道のりをイコールでつなげてやって
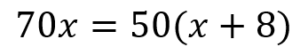
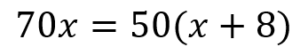
このように方程式が完成しました。
あとは計算あるのみです。
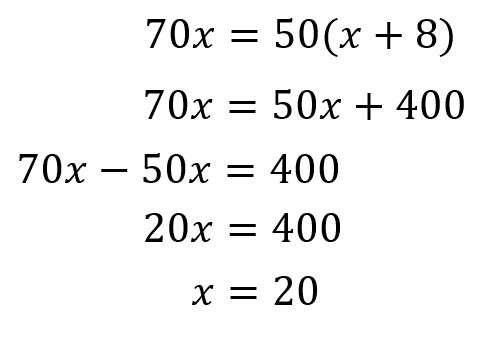
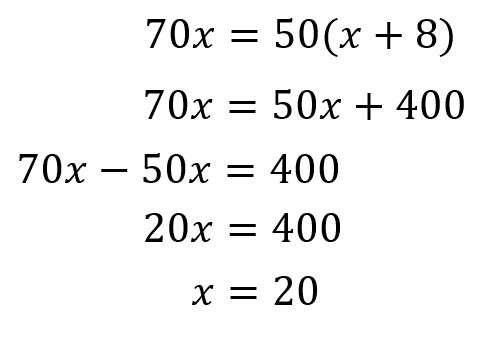
このようにして、兄が出発してから追いつくまでの時間は20分だということが求めれました。
あとは、追いついた地点は家から何mの地点かを求めなくてはいけませんね。
ここでいう追いついた地点というのは、弟と兄が家から進んできた道のりのことです。
すでにそれぞれの道のりは
弟…50(x+8)
兄…70x
と表しているので、この式に先ほど求めたx=20を代入してやれば求めることができます。
どちらの式に代入しても同じ値が出てくるので、なるべく簡単そうな方に代入した方がいいですね。
というわけで、兄の式にx=20を代入してやると、70×20=1400m となります。
よって、2人は1400mの地点で追いつくということが分かりました。
まとめると、この文章問題の答えは
20分後に追いついて、追いついた地点は家から1400mの地点
ということになります。
あれ?
問題文にあった
弟が5㎞離れた公園に向かって家を出発した。
この5㎞って部分は使わないんですか!?
ハイ!
使いません!
5㎞離れていようが、10㎞離れていようが
ゴールするまでの途中で2人は追いついているので
ゴールまでの距離は今回の問題には全く関係ありませんでした。
騙されないでくださいね!
練習問題で理解を深める!
では、以上のことを踏まえて練習問題に挑戦してみましょう。
【問題】
弟が2㎞はなれた駅に向かって家を出発した。それから10分後に姉が自転車で同じ道を追いかけた。弟の歩く速さは分速80m、姉が自転車で走る速さは分速240mでした。このとき、姉が家を出発してから何分後に弟に追いつくかを求めなさい。また、姉が弟に追いついた地点は家から何mの地点か求めなさい。


【追加演習】テストで素早く完璧に解きたいあなたへ!
さて、ここまでのところで「追いつく」についての文章問題は理解してもらえましたか?
この問題は定期テストだけでなく、模試や入試にもよく出てくるパターンとなります!なので、今のうちにしっかりと仕上げておいてもらいたい(‘ω’)ノ
というわけで、2題ほど追加演習を用意しました。
「やり方は分かったけど、数や文章が変わると解けなくなります…」
という学生さんは、この追加演習にチャレンジすることで、どのような表現で出題されても追いつく文章題は確実に満点が取れるようになりますよ^^
演習問題には動画解説もつけておいたので、数学が苦手な方も一緒にがんばっていきましょう!

この課題を活用してみたい!という方にはメールでプリントを送らせてもらっています。
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れますので、ぜひご活用ください^^
【演習課題】一次方程式の利用(追いつく)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
何分で追いつくか?のまとめ
最後に、何分で追いつくか?という速さに関する文章問題のまとめをしておきます。
解法の手順としては
- 追いつくまでの時間を文字で置く
- それぞれの道のりを文字で表す
- 方程式を完成させて解く
この3手順で解くことができます。
この手順を使っていく中でも必ず知っておかないといけないのが
『追いついた場所においては
2人とも進んだ道のりが等しくなる』
ということでしたね。
これらのことをしっかりと覚えておけば、追いつく問題なんてへっちゃらです!
いっぱい練習して、得意問題にしちゃってくださいね♪
方程式の解き方を理解できたら、次は文章問題に挑戦してみましょう。
何分後に追いつくか?速さの問題を解説!←今回の記事




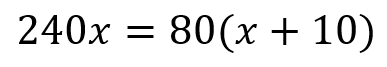
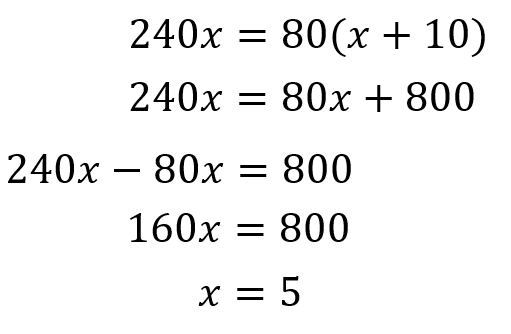













この記事のおかげで問題を解くことができました!
ありがとう
お役に立てて良かったです!!
この記事のおかげで中間テスト乗り切れそうです!!
この記事のおかげでよくわからないところもわかるようになりました。ありがとうございます!
期末テスト頑張ります!!