【連立方程式】池の周りを追いつく速さの文章問題を解説！

今回は中２で学習する連立方程式の単元から

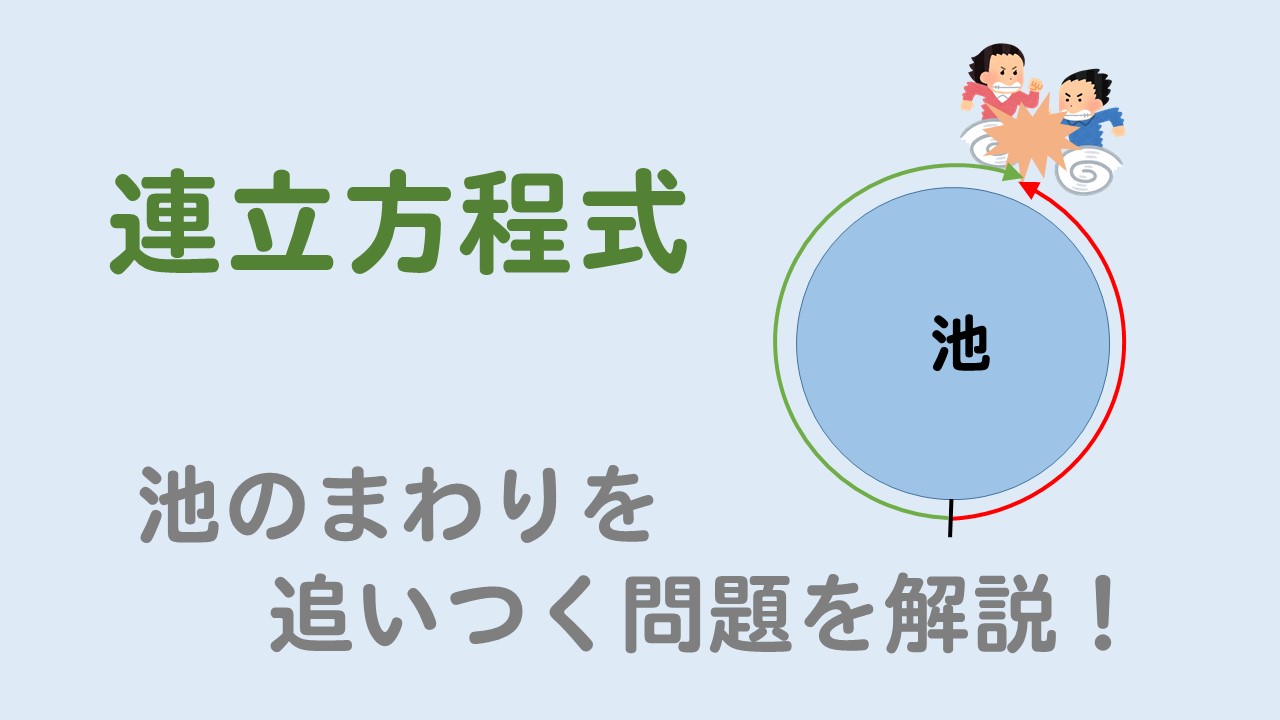
池の周りを追いつく速さの文章問題について解説していくよ！

 

池の周りを追いつく問題というのは

こういう問題ですね。

ちょっと複雑そうに思えるんだけど

ちゃんとポイントをおさえておけば簡単に解くことができます。

では、まずは問題を解く上でのポイントを確認していきましょう！

 

今回の記事はこちらの動画でも解説しています(/・ω・)/

 

池の周りを追いつく問題のポイント！

池の周りを反対方向に進んで、2人が出会うというのは

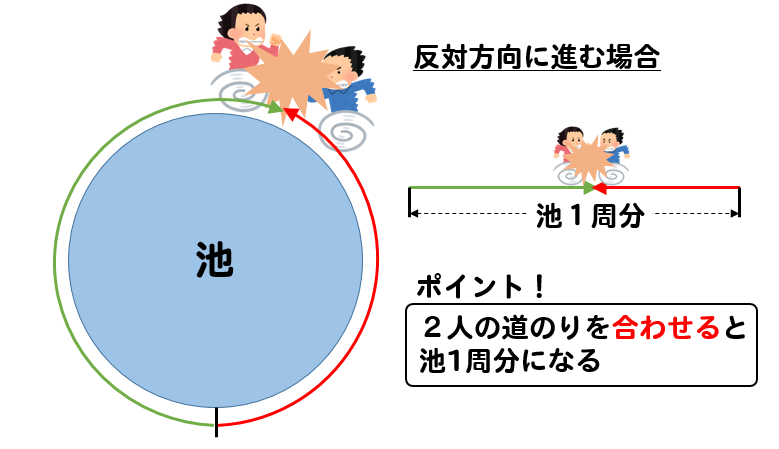
2人の進んできた道のりを合わせると、池1周分の距離になります。

 

 

池の周りを同じ方向に進んで、追いつくというのは

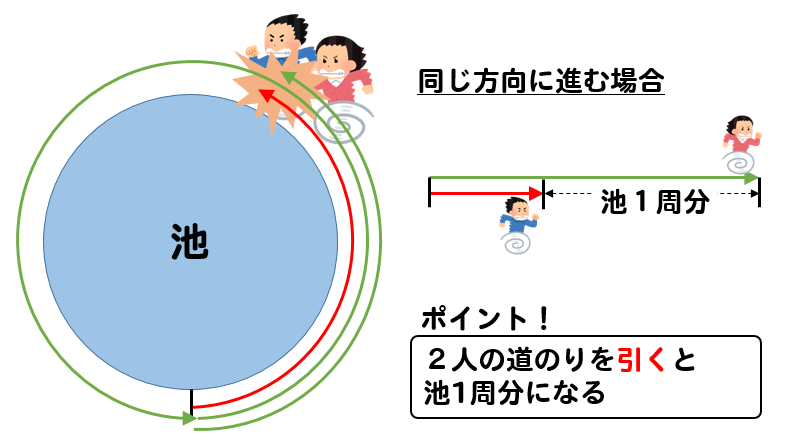
1人が1周遅れになるということなので

2人の進んできた道のりの差が、ちょうど池1周分になるはずです。

 

 

 

これらの特徴を使って、連立方程式を式を立てていきます。

 

池の周りを追いつく問題の解説

 

AさんとB君の速さを求めたいので

それぞれの速さを\(x,y\)としてやります。

 

まずは、2人が反対方向に進む場合から考えていきましょう。

Aさんは、速さが\(x\)で5分間進んでいるので

進んだ道のりは\(x\times 5=5x\)となります。

 

Bくんは、速さが\(y\)で5分間進んでいるので

進んだ道のりは\(y\times 5=5y\)となります。

 

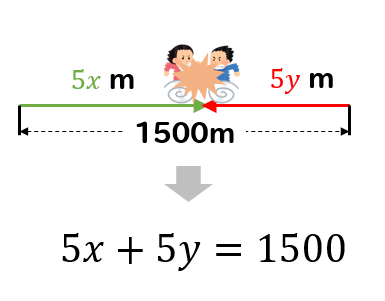
2人が同じ方向に進む場合を考えると

Aさんは、速さが\(x\)で30分間進んでいるので

進んだ道のりは\(x\times 30=30x\)となります。

 

Bくんは、速さが\(y\)で30分間進んでいるので

進んだ道のりは\(y\times 30=30y\)となります。

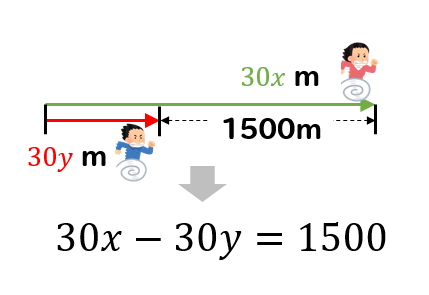
差の式を作るときには

必ず（追いついた方）ー（追いつかれた方）で考えてくださいね。

逆にしちゃうと

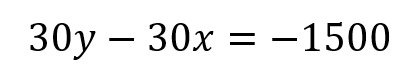
負の数が出てきちゃってややこしくなっちゃうからね(^^;

式を作るときには、この部分を気を付けるようにしましょう。

 

 

以上から式が2本作れたので、連立方程式の完成です。

$$\begin{eqnarray} \left\{ \begin{array}{l} 5x + 5y = 1500 \\ 30x – 30y = 1500 \end{array} \right. \end{eqnarray}$$

 

あとは、この方程式を解いていくだけです。

係数を揃えて、加減法で解いていきます。

$$30x+30y=9000$$

$$30x-30y=1500$$

それぞれの式を足すと

$$60x=10500$$

$$x=175$$

 

\(x=175\)を\(5x+5y=1500\)に代入すると

$$875+5y=1500$$

$$5y=625$$

$$y=125$$

 

よって、Aさんは分速175m、B君は分速125mであることがわかりました！

 

 

それでは、解き方が分かったところで

理解を深めるために練習問題に挑戦してみましょう！

 

練習問題で理解を深める！

【追加】上位を狙うあなたへステキな応用問題を…！

さて、練習問題はバッチリでしたか？？

「こんなの楽勝だぜ、もっと難しいのやらせろや～」

というツワモノ達のために追加で応用演習を用意しましたよ(‘ω’)ノ

 

それがこちらだ！ドンッ！！

文字が見にくい場合は、こちらのプリントを活用してください！

• 演習プリント

 

もうね…問題文が長すぎて読むのがツラいです(^^;)

ですが、入試レベルになるとこういった読解は当たり前、問題を見た瞬間に手を動かしていけるレベルにする必要があります。

というわけで、成績上位、難関校の合格を目指している方は必ず取り組んでおいてください(‘ω’)ノ

 

応用演習やってみたよ～！！

という方には、こちらから詳しい解説動画＆プリントをお渡ししています。

 

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れます＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

 

答えが合っているかどうかだけでなく、動画解説を活用して『立式のポイント』『情報の読み取り方』といったところもチェックしておいてくださいね＾＾

解答を受け取ってくれた方には、引き続きいろんな問題をメールでお届けする予定なのでお楽しみに＾＾

まとめ

お疲れ様でした！

池の周りを追いつく問題では

反対に進む場合、同じ方向に進む場合で

式の作り方が異なってくるので

それぞれの特徴をしっかりと覚えておくことが大切ですね！