【連立方程式】割合を使った全校生徒の増減に関する文章題の解き方を解説！

こんにちは！数スタの小田です。

今回は中2で学習する連立方程式の単元から

割合(％)を使った全校生徒の増減に関する文章問題

について解説していくよ！

今回取り上げていくのは、この2パターンの文章問題です。

割合に関する文章題はこちらの動画でも解説しています(/・ω・)/

割合の表し方を確認

まず、割合の文章問題に挑戦するためには、割合を使った表し方を確認しておく必要があります。

分数で表す方法と小数で表す方法の2パターンありますが、自分の好きな方を利用してください。

この記事では、小数を使って表していきますね。

割合の表し方について詳しく知りたい方は、こちらの記事をご参考ください。

【文字式】割合(パーセント)の問題をわかりやすく解説！

昨年の生徒数を求める問題

それでは、昨年の人数を求めるパターンの問題を解説していきます。

まずは、昨年の男子の人数を\(x\)人、女子の人数を\(y\)人とします。

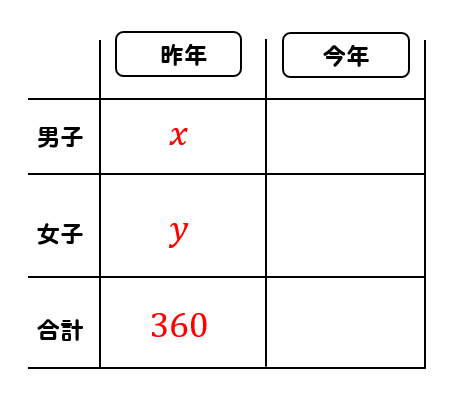
今年の人数はそれぞれ

男子が3％減少

女子が5％増加

全体は2人増加しているので

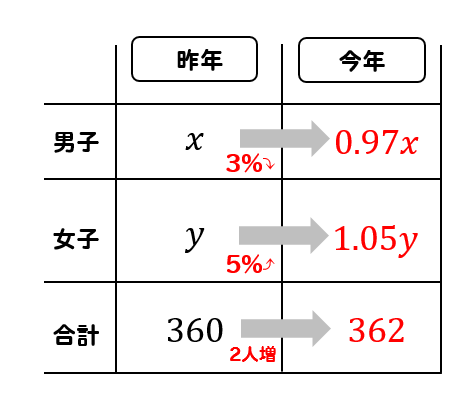
男子は\(0.97x\)

女子は\(1.05y\)

全体は\(362\)人と表すことができます。

よって、昨年の人数と今年の人数から

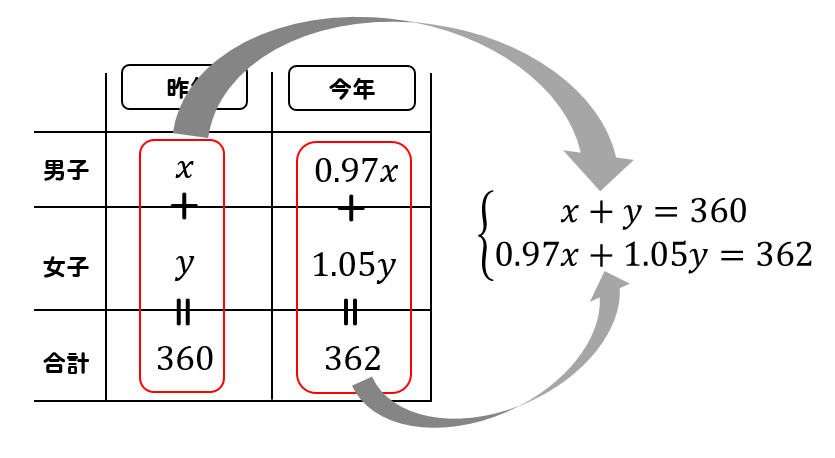
連立方程式が完成します。

$$\begin{eqnarray} \left\{ \begin{array}{l} x + y = 360 \\ 0.97x + 1.05y = 362 \end{array} \right. \end{eqnarray}$$

あとは、この方程式を解いていくだけです。

小数のままだと計算がしにくいので、両辺に100を掛けて小数を消してやります。

$$0.97x\times 100 + 1.05y\times 100 = 362\times 100$$

$$97x+105y=36200$$

小数が消えたところで係数を揃えて加減法で解いてやります。

$$97x+97y=34920$$

$$97x+105y=36200$$

それぞれを引いていくと

$$8y=1280$$

$$y=160$$

\(y=160\)を\(x+y=360\)に代入してやると

$$x+160=360$$

$$x=200$$

よって、昨年の男子の人数は200人、女子の人数は160人となります。

割合の表し方を覚えておけば

式を作ることはそんなに難しくないですね！

今年の生徒数を求める問題

この問題では、今年の人数を求めるように言われています。

なので、今年の男子・女子の人数を\(x,y\)としてしまいたくなりますが

昨年の男子を\(x\)人、女子を\(y\)人としてください。

今年の人数を文字で置いてしまうと、昨年の人数が表しにくくなってしまうんですね。

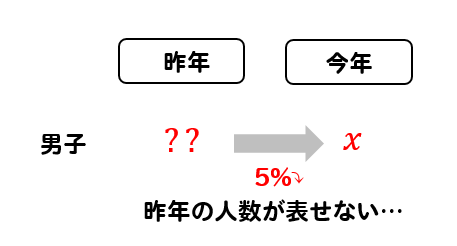
だから、あえて昨年の人数を文字で置きます。

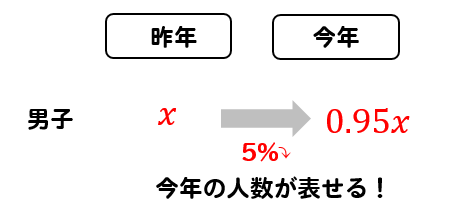
では、昨年の人数を文字で置いて

先ほどの問題と同じように式を作っていきます。

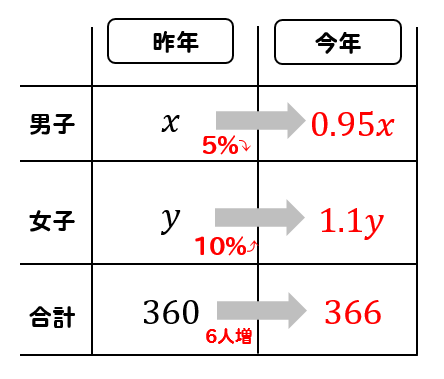
$$\begin{eqnarray} \left\{ \begin{array}{l} x + y = 360 \\ 0.95x + 1.1y = 366 \end{array} \right. \end{eqnarray}$$

方程式が完成したら、計算して解を求めましょう。

すると\(x=200,y=160\)となります。

よっしゃ！これで答えが分かったぜ！

とは、しないように気をつけてください。

この\(x,y\)の値は去年の人数を表したものでしたよね。

今回の問題で知りたいのは今年の人数です！

なので、ここから一手間加えます。

このように昨年の人数から

今年の人数を計算してやりましょう。

よって、今年の男子の人数は190人、女子の人数は176人となります。

【発展】入試レベルの2題を追加しました！

さて、ここまでのところで割合増減の基本はバッチリですね＾＾

この記事に取り組んでくれている方は「文章題をクリアして上位を狙っていくぞ～！！」という、やる気たっぷりの方が多いと思ってます！

なので、定期テストだけでなく模試、学力テストといった総合力が問われるようなテストでもしっかりと得点できるように追加の発展演習を用意しました(‘ω’)ノ

こちらだ！！

どちらも入試問題から抜粋しています。

（1）はまぁ、サクッとクリアできると嬉しいかな＾＾

そんで、（2）はちょっと正解率落ちると思う…けど、チャレンジしてみましょう！

発展演習やってみたよ～！！

という方には、こちらから詳しい解説動画＆プリントをお渡ししています。

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れます＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

答えが合っているかどうかだけでなく、動画解説を活用して『立式のポイント』『情報の読み取り方』といったところもチェックしておいてくださいね＾＾

解答を受け取ってくれた方には、引き続きいろんな問題をメールでお届けする予定なのでお楽しみに＾＾

まとめ

お疲れ様でした！

割合の増減についての文章問題では、割合を使った表し方をしっかりと身につけておくことが大切です。

この問題が苦手だという人の多くは

上手く割合を表すことができていません。

パーセントが苦手だな…と思う方は、まずこちらで理解を深めておいてくださいね。

【文字式】割合(パーセント)の問題をわかりやすく解く方法を解説！

割合の表し方をマスターすれば

この文章問題は簡単に思えるはずです(^^)

とにかく練習あるのみ！

ファイトだー(/・ω・)/