今回は連立方程式の練習問題に挑戦してみましょう!
数学が苦手な人向けに、入試問題から連立方程式の簡単な基礎問題を抜粋してみました。
加減法、代入法でそれぞれ問題を分けているので、自分の練習したい部分を集中的に解いていきましょう!
加減法の練習問題
次の連立方程式を解きなさい。
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}x+y=7 \\4x-y=8 \end{array} \right. \end{eqnarray}}$$
次の連立方程式を解きなさい。
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}2x+y=3 \\3x+2y=-1 \end{array} \right. \end{eqnarray}}$$
次の連立方程式を解きなさい。
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}x+2y=-5 \\8x+3y=-1 \end{array} \right. \end{eqnarray}}$$
次の連立方程式を解きなさい。
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}2x+3y=-2 \\x-2y=6 \end{array} \right. \end{eqnarray}}$$
次の連立方程式を解きなさい。
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}5x+3y=1 \\-2x+y=4 \end{array} \right. \end{eqnarray}}$$
次の連立方程式を解きなさい。
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}4x+3y=1 \\3x-2y=-12 \end{array} \right. \end{eqnarray}}$$
次の連立方程式を解きなさい。
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}4x+5=3y-2 \\3x+2y=16 \end{array} \right. \end{eqnarray}}$$

代入法の練習問題
代入法が苦手だという方は
こちらの記事も参考にしてみてくださいね(^^)
次の連立方程式を解きなさい。
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}2x+y=5 \\y=x-1 \end{array} \right. \end{eqnarray}}$$
次の連立方程式を解きなさい。
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}3x+2y=7 \\x=-2y+1 \end{array} \right. \end{eqnarray}}$$
次の連立方程式を解きなさい。
$$\large{\begin{eqnarray} \left\{ \begin{array}{l}y=-2x+8 \\3x-2y=5 \end{array} \right. \end{eqnarray}}$$
まとめ
お疲れ様でした!
以上の問題がバッチリ解けるようになった方は、連立方程式の基礎はOK!
次は分数、小数を含んだ方程式や文章問題に挑戦していきましょう。
どんどんレベルを上げていくぞー(/・ω・)/



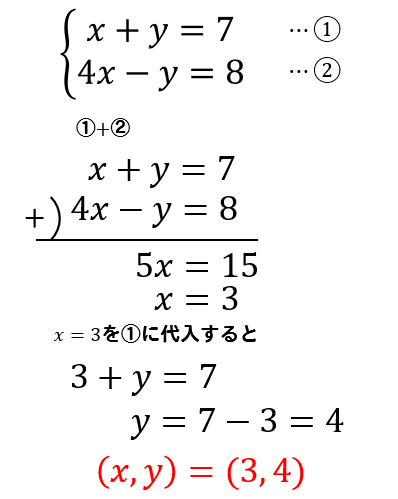
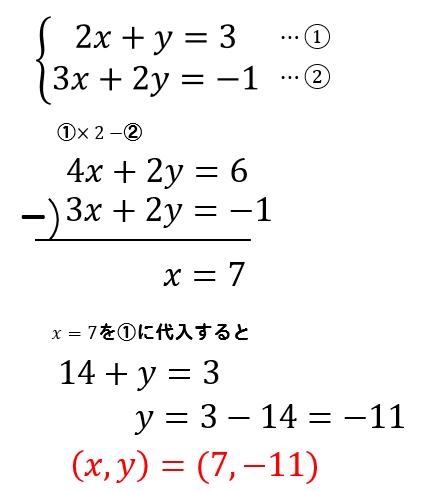
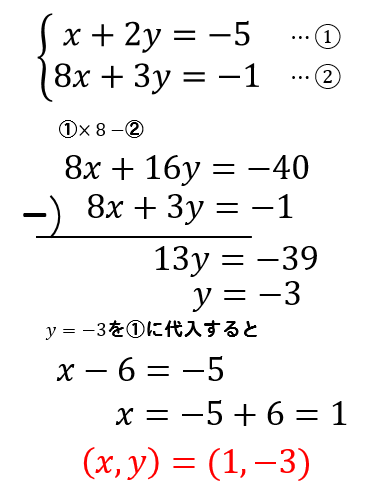
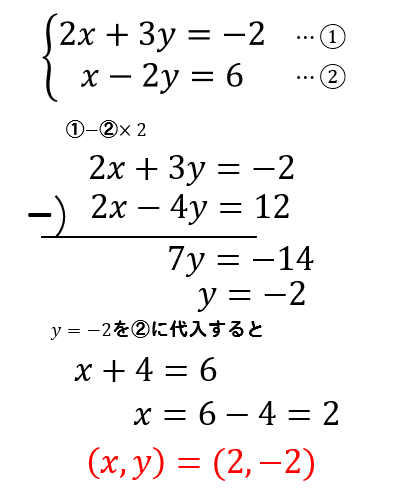
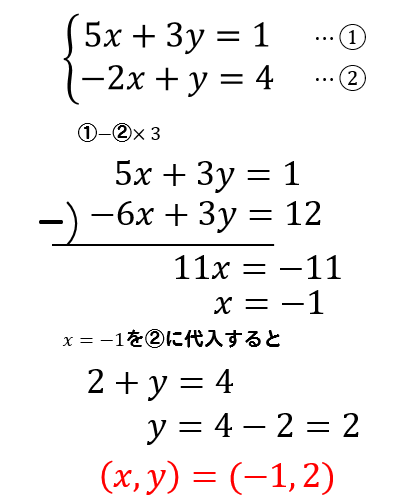
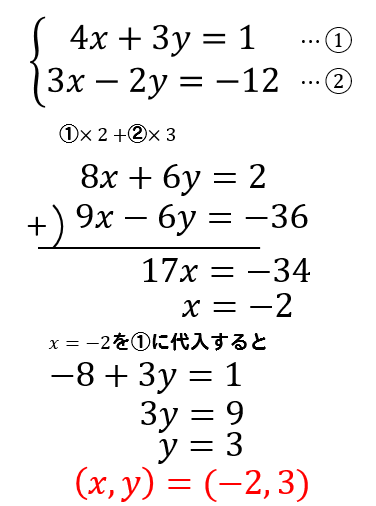

















中学2年生の少年です。テスト前で勉強どうしようか迷ってたけどこの問題のおかげで勉強がめちゃめちゃ捗りました。ありがとうございます( ̄^ ̄)ゞ
いえいえ、お役に立ててよかったです
自分もちゅうに
べんきょうすきになりました。
アリ(´・ω・)(´_ _)ガト♪メシア
先生の問題すきです
ありがとうございます^^