【連立方程式】x+y=3,xy=2の和と積の方程式の解き方は？

今回取り上げる問題はこちらです。

今まで見慣れてきた連立方程式とは見た目がちょっと違うよね(^^;

それでは、今回の連立方程式のように和と積の式になっている場合、どのように解けばよいのか解説していきますね(^^)

YouTubeの動画解説はこちら！

代入法を使って解こう！

連立方程式の解き方には

というものがありましたね。

今回の連立方程式では、足したり引いたりしても文字は消せません。

ということで、代入法を使って計算を進めていきましょう！

代入法を使った解き方手順

和の式を変形して、代入の準備

まずは、和の式を変形して代入の準備を進めます。

\(x=\ldots\)もしくは\(y=\ldots\)の形に変形しましょう。

今回は\(y=\ldots\)の形で話を進めていきますね。

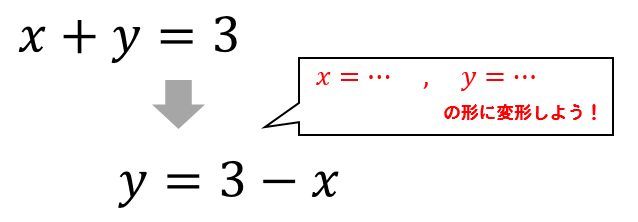
いざ、代入！

それでは、先ほど準備したものを代入しましょう。

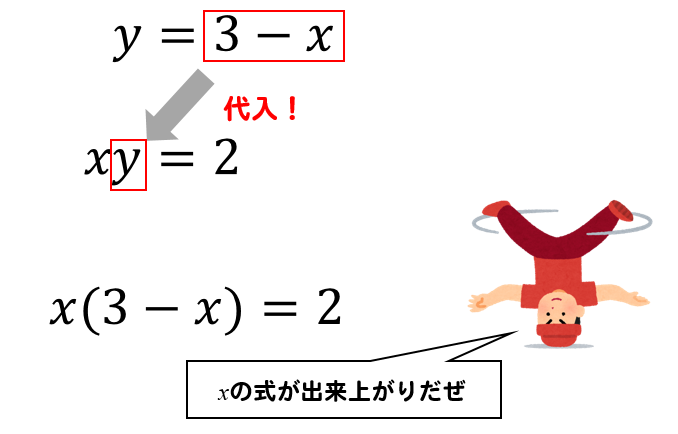
代入することで、文字を1つ減らして一次方程式を作ることができます。

あとは、この方程式を計算していくだけですね(^^)

代入した式を計算！

先ほど作った式を計算していきましょう。

$$\large{x(3-x)=2}$$

$$\large{3x-x^2=2}$$

$$\large{-x^2+3x-2=0}$$

両辺に（－1）を掛けて符号をチェンジします。

$$\large{x^2-3x+2=0}$$

$$\large{(x-2)(x-1)=0}$$

$$\large{x=2,   1}$$

このように\(x\)の値が2つ求まりました。

それぞれの値を式に代入して、\(y\)の値も求めましょう。

\(x=2\)のとき、\(x+y=3\)に代入すると

$$\large{2+y=3}$$

$$\large{y=1}$$

\(x=1\)のとき、\(x+y=3\)に代入すると

$$\large{1+y=3}$$

$$\large{y=2}$$

よって、連立方程式の解は

$$\large{x=2, y=1}$$

$$\large{x=1, y=2}$$

となります。

完了！

そんなに難しいものではありませんでしたね(^^)

最後に演習問題に挑戦して理解を深めておきましょう！

演習問題に挑戦！

まとめ

お疲れ様でした！

和と積の式を連立方程式で解く場合には代入法を活用してみましょう。