今回は比例式の解き方について説明していきます。
比例式を解くためには、方程式の解き方について知っておく必要があります。
方程式の解き方なんだっけ？
という方はこちらを先に読んでみてくださいね！
それでは、比例式の解き方について確認していきましょう！
今回の記事は、こちらの動画でも解説しています。
比例式とは
$$ \LARGE{a:b=c:d}$$
こういった比の式のことを比例式といいます。
左の\(a:b\)と右の\(c:d\)が等しいということを表した式のことです。
そして、特徴として
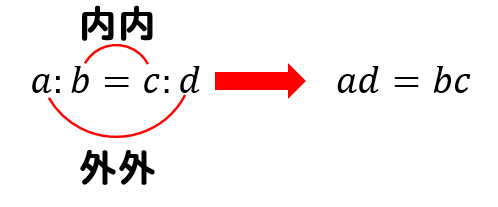
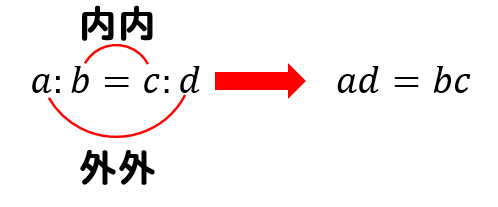
このようにイコールを挟んで
内にある数どうし
外にある数どうしを掛けると
それぞれは同じ数になるという性質があります。
この性質を使って計算問題を解いていくわけなので、しっかりと覚えておきましょう！
比例式の解き方
比例式の計算とは、このように出題されます。
問題
次の\(x\)の値を求めなさい。
$$\LARGE{4:3=x:9}$$
こういった問題を解くときに
小学生の時には
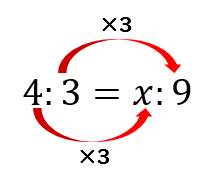
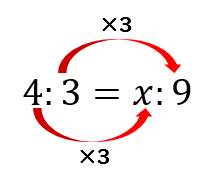
数字が揃っている右側同士を見て、何倍されているかを調べます。
今回は3倍されていることが分かるので、左側も3倍されることになるので
答えは4×3で12となります。
今までは、このように習ったとおもうのですが
中学では、この方法だと対応しづらい問題も出てくるので
上で紹介したような『内内外外』の性質を使って考えていきましょう。
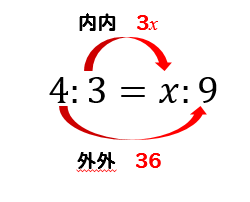
内内を掛けると3×x＝3xとなります。
外外を掛けると4×9＝36となります。
それぞれが同じ値になるんで、3x＝36という方程式ができあがります。
あとはそれを計算するだけですね！
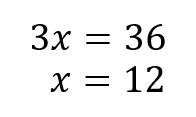
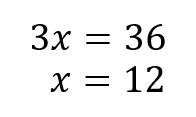
この比例式だけ見ていると
小学校で習ったやり方の方が簡単に思えてしまうのですが
『内内外外』の性質を使った解き方は次のような問題で力を発揮します。
分数が出てくる比例式の計算
問題
次の\(x\)の値を求めなさい。
$$\LARGE{2:\frac{2}{5}=x:1}$$
このように見た目が複雑になってきたり数字が揃ってる同士を比べてみても、何倍になっているかが分かりにくいときは『内内外外』の本領発揮です。
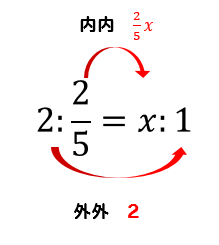
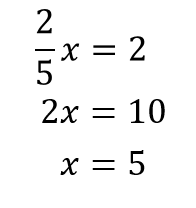
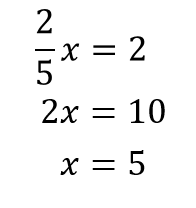
複雑な比例式であっても、簡単な方程式を解くことで答えを出すことができましたね！
他にも次のような比例式でも役に立ちますよ！
かっこがついている比例式の計算
問題
次の\(x\)の値を求めなさい。
$$\LARGE{4:5=(x-3):15}$$
このようにかっこがついている比例式においても『内内外外』は大活躍します。
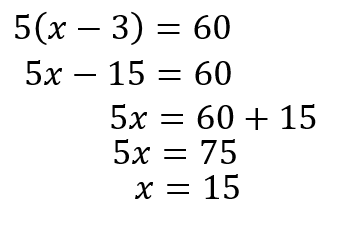
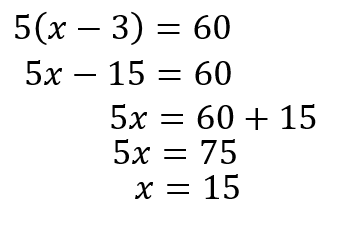
『内内外外』で掛けていくときには、必ずかっこごと掛けて分配法則で計算していきましょう。
このように比例式は『内内外外』の性質を使いながら解いていくと
どんな複雑な比例式が出てきても解くことができますね！
それでは、計算方法が分かったところでいくつか練習問題をやってみましょう。
練習問題に挑戦！
比例式の解き方を身につける為に練習問題に挑戦してみましょう！
問題
次のxの値を求めなさい。
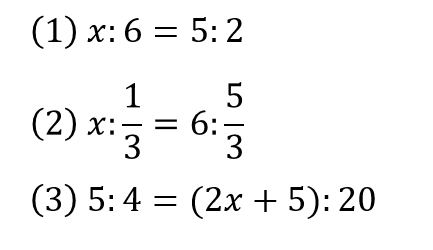
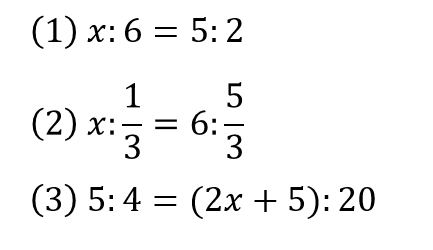
できましたか？
それでは確認してみましょう。
内内の掛け算で6×5＝30
外外の掛け算でx×2＝2x
それを方程式にして解くと
内内の掛け算で\(\frac{1}{3}\times 6=2\)
外外の掛け算で\(x\times \frac{5}{3}＝\frac{5}{3}x\)
それを方程式にしていくと
内内を掛けると4×(2x＋5)＝4(2x＋5)
外外を掛けると5×20＝100
それを方程式にしていくと
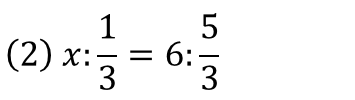
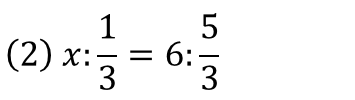
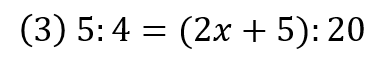
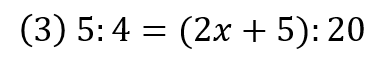
以上！
練習問題でした。
全部正解できましたか？
比例式の計算 まとめ
比例式の計算では、とにかく
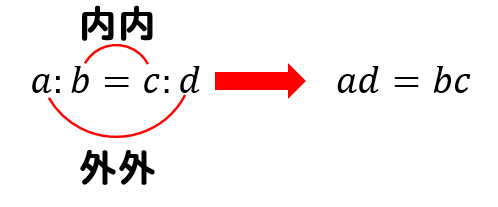
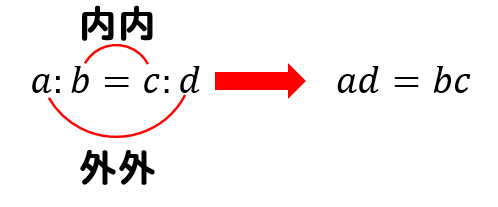
内内を掛けたものと、外外を掛けたものは同じ値になる。
という『内内外外』の性質をしっかりと覚えておくことが大切です。
逆に言えば、この性質だけしっかりと覚えておけば大丈夫！ということでもあります。
たくさん練習して身につけておきましょう！
比例式の文章問題に関しては、こちらの記事で解説しているので参考にしてみてください＾＾
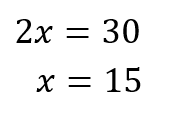
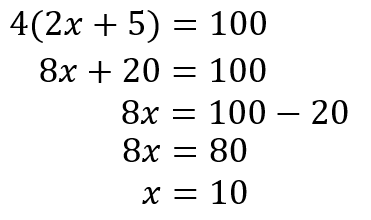
ホントに役に立ちました！今日習ったばっかで、あまり理解が出来なかったんです（笑）でもこのサイトのおかげでマジで理解出来ました！！ありがとうございます(*˘︶˘*).:*♡
こちらこそ、嬉しいコメントありがとうございます(^^)
引き続き勉強がんばってくださいね！