【二次方程式】解の公式を利用した解き方、bが偶数のときに使える公式とは？例題を使って解説！

今回は、中3で学習する二次方程式の単元から

解の公式を利用した解き方

について解説していくよ！

二次方程式の解き方は、大きく分けて4パターンあります。

この中から

すっごく万能な解き方である

解の公式を利用した解き方について学んでいきましょう！

今回の記事はこちらの動画でも解説しています(/・ω・)/

解の公式を使った解き方

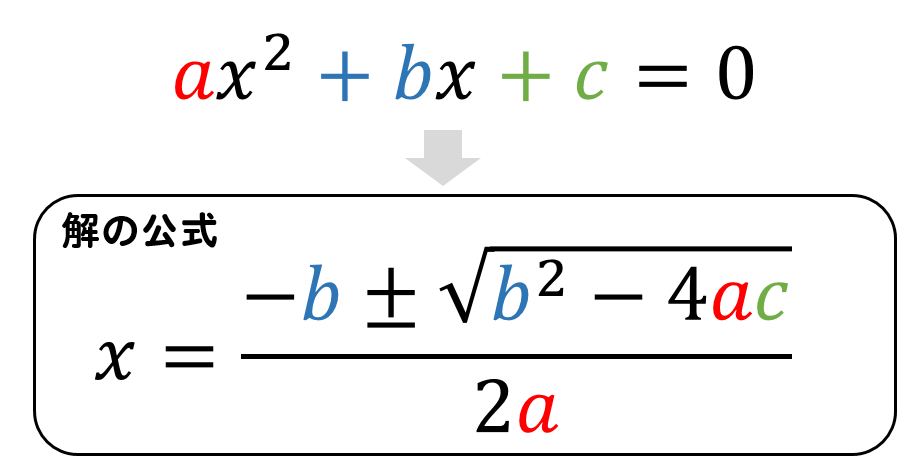
\(x^2\)の係数を\(a\)

\(x\)の係数を\(b\)

定数を\(c\)とするとき

解の公式と呼ばれる以下の式に

$$\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

にそれぞれの値を代入することで、二次方程式の解を求めることができます。

例えば

$$\LARGE{5x^2-x-2=0}$$

という二次方程式を解く場合

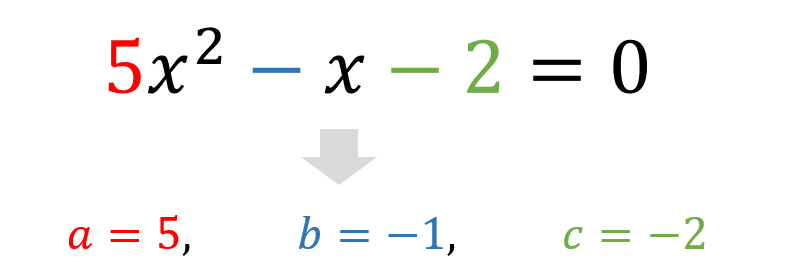
\(a,b,c\)の値をそれぞれ読み取って

解の公式に代入します。

$$x=\frac{-(-1)\pm \sqrt{(-1)^2-4\times 5 \times (-2)}}{2\times 5}$$

$$=\frac{1\pm \sqrt{1+40}}{10}$$

$$=\frac{1\pm \sqrt{41}}{10}$$

このように二次方程式の解を求めることができます。

解の公式…

なんか複雑だから嫌だよ

覚えるのも苦手だし

って思うかもしれませんが

解の公式って、とーーーーーっても役に立つ優れものなんですよ！

二次方程式には、平方根の考え方や因数分解を使った解き方がありましたよね。

それらは解き方自体はとっても簡単なモノでしたが、ちょっとした欠点があります。

それは、方程式の種類によっては使えない

ということです。

その点、解の公式を使った解き方は

どんな方程式であっても解くことができるんですね。

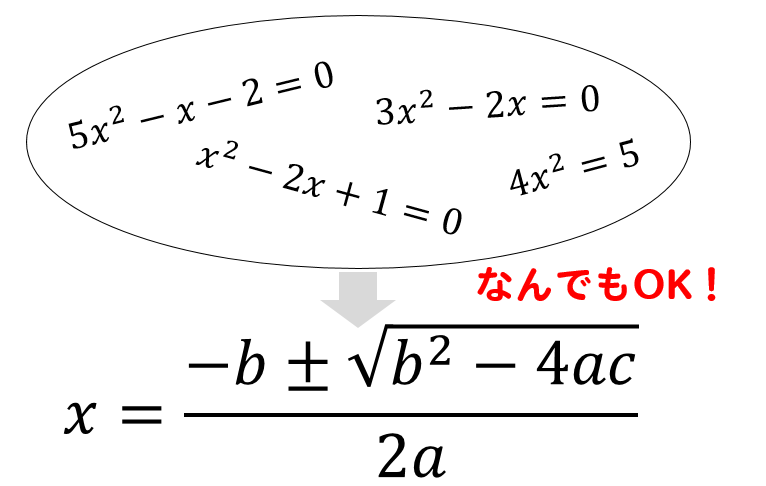
少し複雑だけど、超万能型だよね！

なので、二次方程式を解くときには

平方根、因数分解を使って解くことができないか考える。

ムリそうであれば解の公式を利用して解く。

という感じで

「解の公式さん、なんとかお願いします」

困ったときのお助けマンとして活躍してくれます。

というわけで、必ず覚えておきましょう！

解の公式の証明

そもそも何で

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

こんな式に代入して、答えが求めれるのでしょうか。

それは

$$ax^2+bx+c=0$$

の式を変形していくことで導けるので

式変形の過程を解説していきますね。

平方完成の考え方を利用して、式を変形していきます。

まずは、cを右辺に移項

$$ax^2+bx=-c$$

左辺を平方完成していく上で邪魔になる\(x^2\)の係数\(a\)で両辺を割ります。

$$x^2+\frac{b}{a}x=-\frac{c}{a}$$

\(x\)の係数である\(\frac{b}{a}\)の半分の2乗を両辺に加えます。

$$x^2+\frac{b}{a}x+\left (\frac{b}{2a}\right )^2=-\frac{c}{a}+\left (\frac{b}{2a}\right )^2$$

左辺を因数分解して、右辺を計算してまとめます。

$$\left( x+\frac{b}{2a}\right )^2=-\frac{c}{a}+\frac{b^2}{4a^2}$$

$$\left( x+\frac{b}{2a}\right )^2=-\frac{4ac}{4a^2}+\frac{b^2}{4a^2}$$

$$\left( x+\frac{b}{2a}\right )^2=\frac{b^2-4ac}{4a^2}$$

ここから平方根の考え方を利用して、式を変形させます。

$$x+\frac{b}{2a}=\pm\sqrt{\frac{b^2-4ac}{4a^2}}$$

$$x+\frac{b}{2a}=\pm\frac{\sqrt{b^2-4ac}}{2a}$$

$$x=-\frac{b}{2a}\pm\frac{\sqrt{b^2-4ac}}{2a}$$

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

というわけで

解の公式の形が導けることがわかりましたね！

この変形がテストに出されるようなことはないと思いますが

式変形の過程を理解できるようにはしておきましょう。

解の公式を使って解く場合の注意点！

次に、解の公式を利用して二次方程式を解いていくときに

よく質問されることについてまとめておきます。

分母がマイナス、aがマイナスになる場合

$$-4x^2+5x-1=0$$

このようにaがマイナスになっている場合

解の公式を利用していくと

$$x=\frac{-5\pm\sqrt{25-16}}{-8}$$

というように分母にマイナスがでてきてしまい

符号をどのように処理していけば良いかわからなくなってしまう人が多いです。

aがマイナスのときには

両辺に\(-1\)を掛けることで符号を変えてから解の公式を利用するようにしましょう。

$$(-4x^2+5x-1)\times (-1)=0\times (-1)$$

$$4x^2-5x+1=0$$

$$x=\frac{5\pm\sqrt{25-16}}{8}$$

$$x=\frac{5\pm\sqrt{9}}{8}$$

$$x=\frac{5\pm 3}{8}$$

$$x=1, \frac{1}{4}$$

約分ができる場合とできない場合

解の公式を利用したときに

約分できる場合には、ちゃんと約分して答えを求めないといけません。

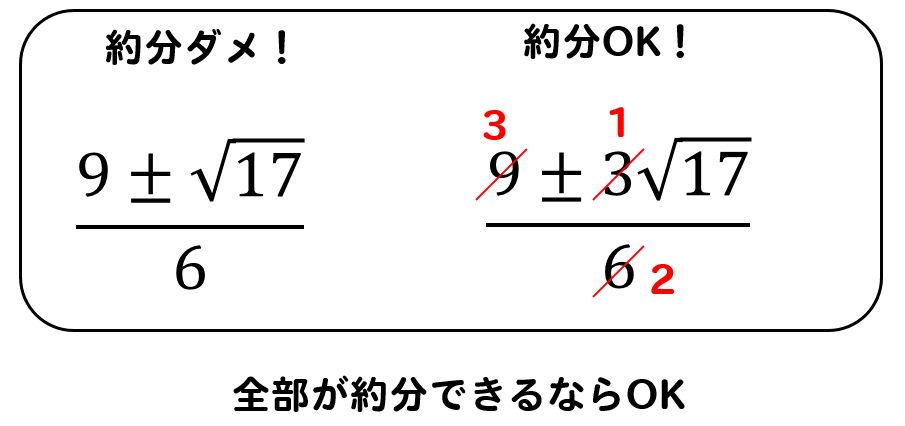
このように、すべてが約分できる場合にはしてやりましょう。

このような約分はしないように気を付けてくださいね！

解の公式を使うときの例題を解説！

それでは例題を通して、解の公式の理解を深めていきましょう！

bが偶数のときに使える解の公式(簡略バージョン)とは？

解の公式には、bが偶数のときにだけ使える簡略バージョンが存在します。

このように簡略バージョンでは、ちょっとだけ計算が楽にできます。

例えば、\(x^2+10x+6=0\)を簡略バージョンの解の公式に当てはめてみるとどうなる解説していきます。

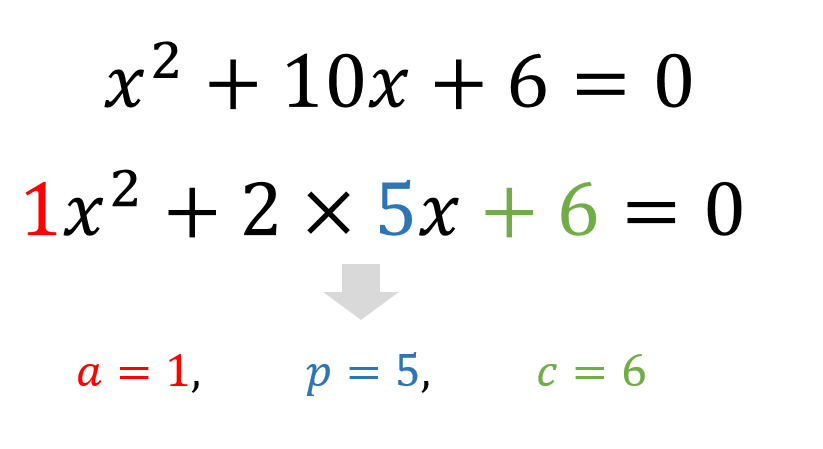
\(x\)の係数が偶数であれば、\(2\times 〇\)の形にしてやって

〇部分の値を\(p\)とします。

そして、それぞれの値を簡略バージョンの解の公式に当てはめると

$$x=\frac{-5\pm \sqrt{5^2-1\times 6}}{1}$$

$$x=-5\pm \sqrt{19}$$

となります。

簡略バージョンを使わない、通常の解の公式で解いた場合

$$x=\frac{-10\pm \sqrt{10^2-4\times 1\times 6}}{2\times 1}$$

$$x=\frac{-10\pm \sqrt{76}}{2}$$

$$x=\frac{-10\pm 2\sqrt{19}}{2}$$

$$x=-5\pm \sqrt{19}$$

比較してみると、計算の手間は明らかですね。

b部分が偶数であれば、ぜひ簡略バージョンも活用してみてください。

ただし、この簡略バージョンを覚えないと解けない問題というのはありません。

ちょっと計算が楽になるだけなので

覚えるのが嫌だな…という人は通常の解の公式だけを活用できれば大丈夫です！

【追加演習プリント】自宅学習で伸ばしたい方へ！

この記事を読んでくださっている保護者さんの方へ！

ここで紹介してる例題を一通り理解してもらえれば、解の公式を利用した解き方はバッチリです＾＾

あとは実戦演習を通して、手本がなくてもスラスラと解けるようにしておいてもらいたいです！

というわけで、自宅学習で活用してもらいたい演習プリントを用意しました。

ここで取り上げている問題はこちら！

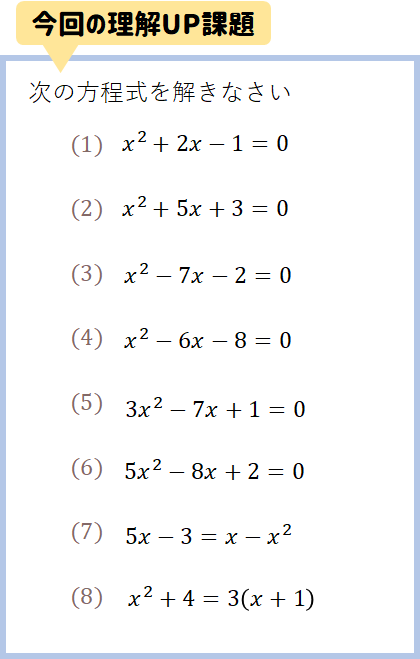
問題＆解説をプリント形式で用意しているので、こちらを印刷してお子さんに渡してあげてください＾＾

10分ほどで取り組める分量になっているので、スキマ時間を活用して二次方程式の理解度を高めておきましょう！

勉強のスタート時に小テストとして取り組んでみると、イイ感じに集中力が高まって、その日の学習がスムーズになってくるかもしれませんね(‘ω’)ノ

追加演習をやってテストの点数をUPさせたい方には、課題プリントをメールで送らせてもらっています。

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

まとめ

お疲れ様でした！

今回は二次方程式の解の公式についての解説でしたが

解の公式は、覚えるのがちょっと面倒だけど

その分、万能でとっても役に立つものだってことは分かってもらえたかな？

高校生になっても

ずーーーーーっと活躍する公式だから

今のうちに完全マスターしておこう！

ファイトだー(/・ω・)/

二次方程式の解き方4パターンについてはこちらをどうぞ！

• 平方根の考えを利用して解く
• 因数分解を利用して解く
• 解の公式を利用して解く　⇐ 今回の記事
• 平方完成を利用して解く