今回は中1で学習する「空間図形」の単元から
球の体積・表面積の求め方について解説していくよ！
球というのは
こういったボール状の形をしているものだよね！
実は、ちょっとだけ公式が複雑だったりします(^^;
だけど、公式を覚えることができれば楽勝の問題になっちゃいます。
今回は、複雑な公式の覚え方についても紹介していくので
この記事を通して、球をマスターしていこう！
Contents
球の体積・表面積の公式
球の体積
$$\LARGE{\frac{4}{3}\pi r^3}$$
$$\large{\frac{4}{3}\pi \times 3^3}$$
$$\large{=\frac{4}{3}\pi \times 27}$$
$$\large{=36\pi (cm^3)}$$
球の表面積
$$\LARGE{4\pi r^2}$$
$$\large{4\pi \times 4^2}$$
$$\large{=4\pi \times 16}$$
$$\large{=64\pi (cm^2)}$$
公式を覚えることができたら
\(r\)の部分に半径の値を当てはめてやるだけでOKです！
計算自体は簡単＾＾
あとは、この複雑な公式を正確に覚えれるかどうかだけですね。
ということで
私が学生の頃から使われている
球の公式を覚えるための語呂合わせを紹介していきます！
覚えにくいから語呂合わせで覚えよう！
球の体積公式を語呂合わせ
身の上に心配ある人が参上！
どんな状況やねん！とツッコミを入れたくなるのですが
公式を覚えるための語呂合わせです。
我慢してください。
球の表面積公式を語呂合わせ
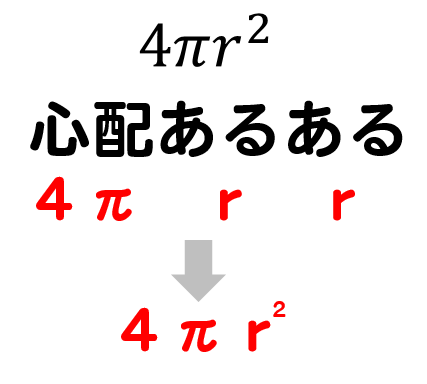
心配あるある～ 言いたい～♪
お笑い芸人さんのネタを思い浮かべながら覚えましょう。
あるある言いたい～♪
参考：RGさんのあるあるネタ
このように語呂合わせで覚えてしまえば
複雑な公式であっても、その場で思い出すことができますね！
私は今でも語呂合わせで思い出すことがありますｗ
あ！
語呂合わせで公式は覚えたけど
どっちが体積で、どっちが表面積だっけ？
というようにごちゃごちゃになっちゃう人も多いです。
そういう人は、体積と表面積の単位に注目しましょう。
体積の単位には\(cm^3\)、\(m^3\)というように3乗がついているよね。
だから、公式にも\(\displaystyle \frac{4}{3}\pi r^3\)というように3乗がある。
面積の単位には\(cm^2\)、\(m^2\)というように2乗がついているよね。
だから、公式にも\(4\pi r^2\)というように2乗がある。
このように3乗、2乗を単位と関連付けておくことで
どっちがどっちだっけ？
というような悩みは解消されるはずです。
演習問題で理解を深めよう！
それでは、問題を通して球の公式をしっかりと身につけていきましょう！
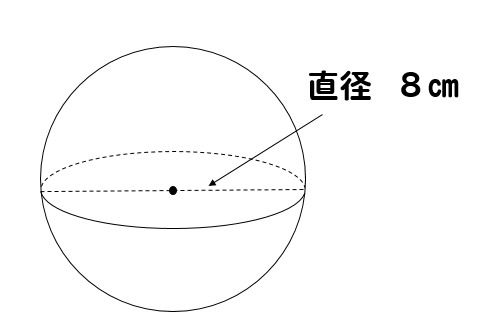
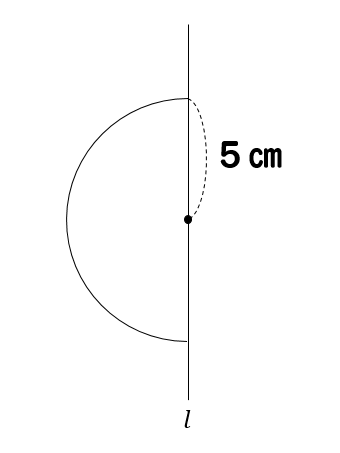
半球の体積・表面積は？
それでは、ちょっとした応用問題について考えてみましょう。
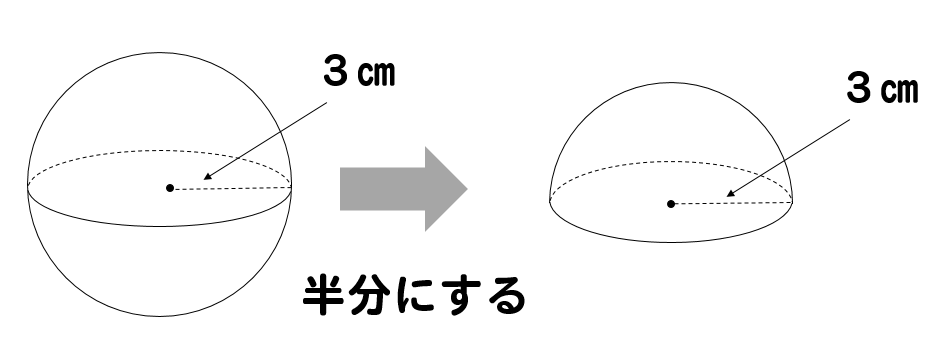
球を半分に切った半球
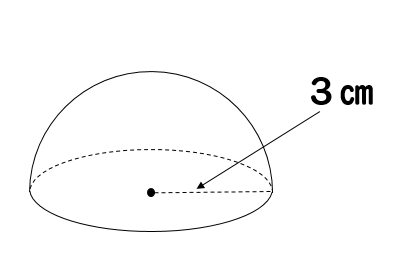
この半球の体積と表面積は、どのように求めれば良いのでしょうか。
半球の体積を求める方法
元の球の状態の体積を求めて半分にしてやります。
$$\frac{4}{3}\pi \times 3^3=36\pi$$
$$36\pi \times \frac{1}{2}=18\pi (cm^3)$$
まぁ、半球だからといって特別な公式があるわけではありませんね！
だけど、表面積はちょっと注意が必要です。
半球の表面積を求める方法
半球の表面積を求める場合には
半球の局面部分
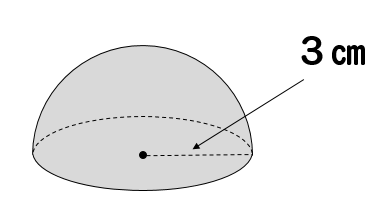
$$4\pi \times 3^2 \times \frac{1}{2}=18\pi$$
半球の底部分
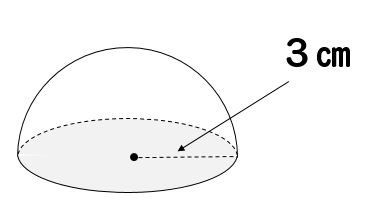
$$\pi \times 3^2=9\pi$$
それぞれを求めて足してやる必要があります。
$$\large{18\pi +9\pi=27\pi(cm^2)}$$
底部分を求め忘れるケースが多いので注意が必要です。
まとめ
お疲れ様でした！
球の公式は覚えれましたか？
なかなか覚えれないよーという方は
ぜひ語呂合わせも利用してみてくださいね！
体積
$$\large{\frac{4}{3}\pi r^3}$$
（身の上に心配ある参上！）
表面積
$$\large{4\pi r^2}$$
（心配あるある）
いいい
ありがととととと！