ちょうちょ型図形の角度は？求め方を徹底解説！

今回は、ちょうちょ型の図形には

どんな特徴があるのかについて紹介していきます。

 

星形の図形とブーメラン型の図形については、こちらをご参考ください！

【星形の角度】内角の和の求め方を問題解説！

ブーメラン型角度の求め方を解説！

 

今回の記事はこちらの動画でも解説しています(/・ω・)/

 

 

ちょうちょ型図形の特徴とは？

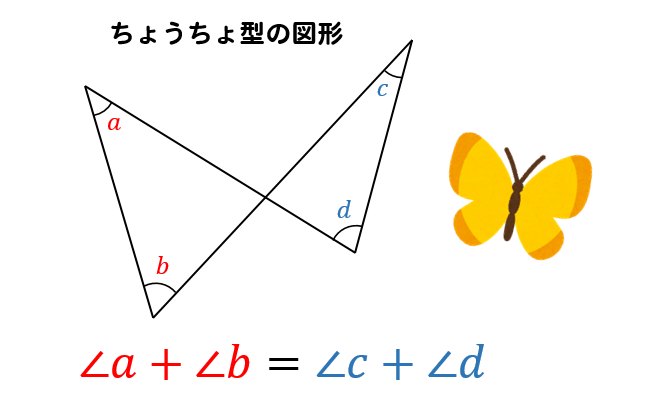
ちょうちょ型図形には

上のように\(∠a+∠b=∠c+∠d\)となります。

ちょうちょの左羽の角を足すと、右羽の角を足したものと等しくなるという性質です。

 

この性質を覚えておくと

いろんな問題で活用できるので

とても便利です(^^)♪

 

 

でも…

なんでこんな性質があるの？

納得できないまま問題に挑戦するのは嫌だよね

ということで、問題を紹介する前に

まずはこの性質の理由から解説していきます。

なぜこのような性質があるのか？

この性質を説明するために

予備知識として知っておいてもらいたいのが

三角形の外角の性質です。

 

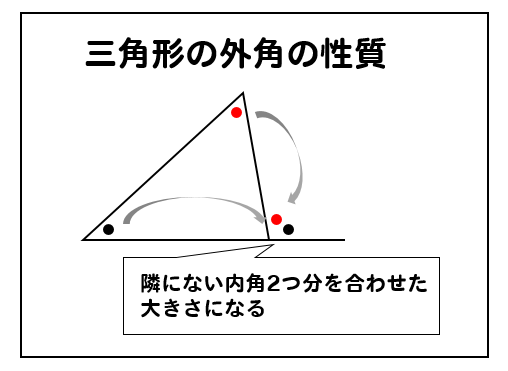
三角形の外角の性質とは、上の画像のように

隣にない内角2つ分を合わせると外角を求めることができる

というものです。

 

 

この性質を利用して

ちょうちょ型の図形を見てみると

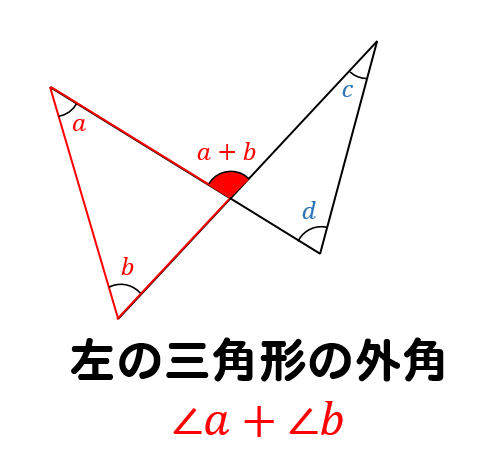
左の羽部分の三角形に注目した場合

外角を\(∠a+∠b\)と表してやることができます。

 

 

同様に、右の羽部分の三角形に注目すると

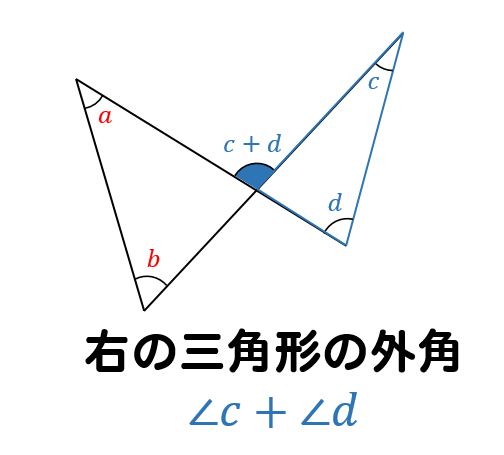
外角は\(∠c+∠d\)と表すことができます。

 

 

２つのことをまとめると

同じ角を\(∠a+∠b\)、\(∠c+∠d\)の2通りで表すことができました。

当然、２つは同じ大きさの角であるので

$$∠a+∠b=∠c+∠d$$

になるということが分かりました！

 

 

という訳で

ちょうちょ型の図形では

このような性質があるということになります。

以降、問題を解く場合にはどんどん活用していきましょう。

 

では、ちょうちょ型の角度の問題とは

一体、どのようなものが出題されるのでしょうか。

 

ちょうちょ型の問題に挑戦！

まずは基本的な問題から見ていきましょう。

 

 

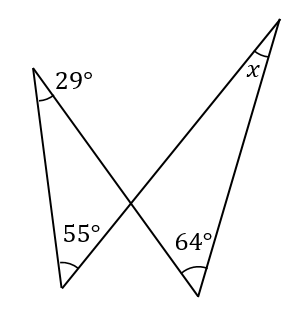
ちょうちょ型の図形だ！！

ってことに気づけたら

ちょうちょ型の性質を利用していきましょう。

すると

$$29+55=x+64$$

という式が作れます。

あとは、この方程式を解いていけば\(x\)の値を求めることができます。

$$x+64=84$$

$$x=84-64$$

$$x=20$$

 

ちょうちょ型の性質を知っておけば

とっても簡単な問題でしたね！

 

 

それでは、次はちょっと応用問題も見ていきましょう。

 

 

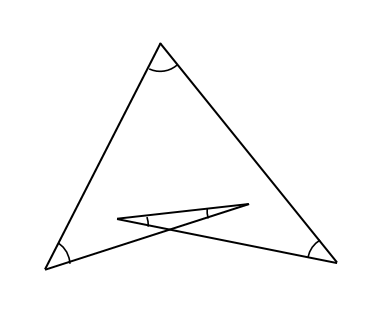
ん？

どこにも角の大きさが書いていないのに

どうやって角の和を求めるんじゃいっ！！

 

って思いますよね。

それがね、ちょうちょ型の性質を利用していくと

わかっちゃうんですよね！角の和が！

 

まずは、この図形に補助線を引いて

ちょうちょ型の図形を作ってやります。

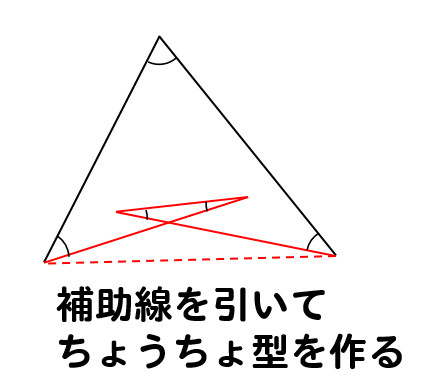
↑赤い線で囲まれている図形が、ちょうちょ型になっているよね。

 

 

すると、このように

上の三角形の2つの角の和が

下の三角形の2つの角の和と等しくなります。

 

 

つまり

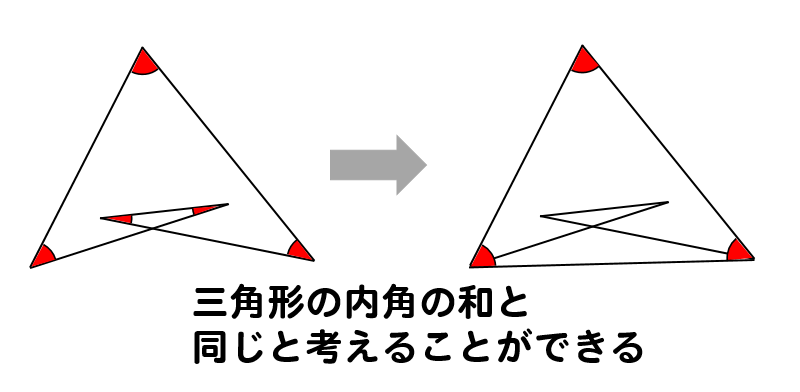
問題で与えられている角の和というのは

角の場所を動かして考えることで

三角形の内角の和を求めることと等しくなります。

 

 

よって、この問題の答えは180°となります。

 

 

どこにも角の大きさが書いていない問題ですが

ちょうちょ型を使って、等しくなる角を見つけていくことで

分かりやすい図形に変換して角の和を求めることができます。

 

この考え方を利用していくと

 

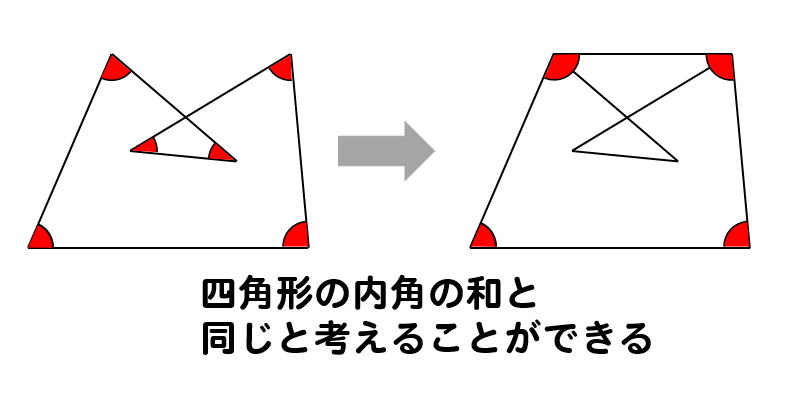
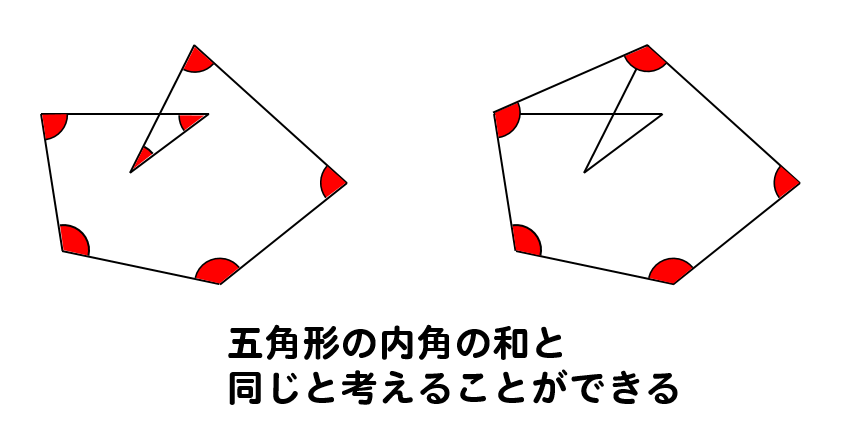
このような複雑な図形でも

四角形や五角形などの分かりやすい図形に変換して考えることができます。

 

 

初見で解くのは難しい問題ですが

やり方を知っている人にとっては

ラッキー問題なくらい簡単に解くことができます。

必ず、この記事を通して理解を深めておいてくださいね！

ちょうちょ型の角　まとめ

お疲れ様でした！

ちょうちょ型の図形の性質はもうバッチリでしょうか？

 

覚えておくと

いろんな問題で活用できるので

ぜーーーったいに覚えておきましょう！

これで得点アップ間違いなしだっ！

ファイトだー(/・ω・)/