高校生になって、一番最初に戸惑うのは…
因数分解のたすき掛け
ではないでしょうか。
高校数学のレベルの高さを感じてしまいます(^^;)
だけど、しっかりと練習を積むことで
誰だってスラスラと解けるようになっちゃいます!
今回の記事では、たすき掛けを使った因数分解の解き方を伝授。
そして、たくさん練習問題を用意しておいたので
実践を通して、理解を深めていきましょう!
たすき掛けの因数分解【やり方】
次の式を因数分解しなさい。
$$3x^2+5x+2$$
まずは、\(x^2\)の係数である\(3\)に注目!
掛けて\(3\)になる数を考えると、\(1\)と\(3\)が見つかりますね。
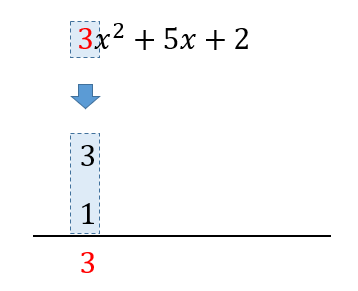
次に、定数項である\(2\)に注目します。
掛けて\(2\)になる数を考えると、\(1\)と\(2\) や\(-1\)と\(-2\)といった組み合わせが考えられます。
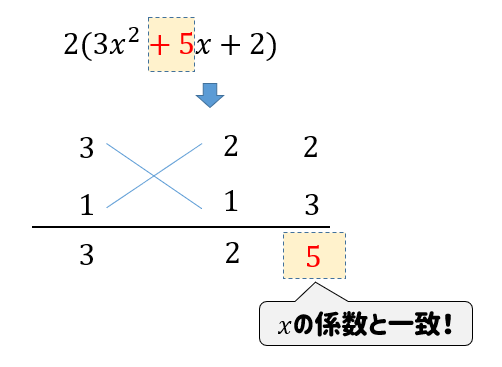
それらの数の組み合わせを次のように書いて、たすきのように斜めに掛け算をしていきます。
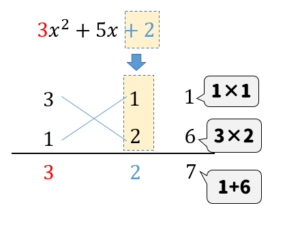
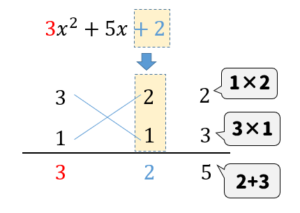
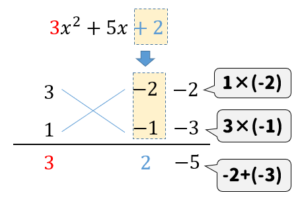
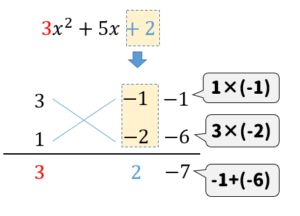
そして、それぞれ出てきた数を足したものに注目します。
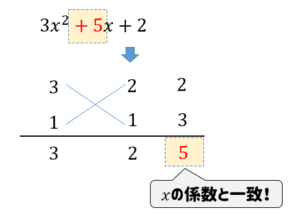
すると、この中から\(x\)の係数と一致しているものが見つかりますね!
そしたら、この数の組み合わせを利用して

このように因数分解をすることができます。
これが「たすき掛けの因数分解」と呼ばれるやり方です。
初めのうちは、なかなか一致する組み合わせが見つけれず苦労します(^^;)
まぁ、そこはたくさんの練習問題をこなしていくことで経験値がたまり、いつの日かサクッとできるようになってきます。
というか、サクッと解けるようにならなくては今後の高校数学は苦労することになっちゃうので…
ここは何としてもマスターしていきたいですね!
次の章では、たすき掛けの因数分解の発展バージョンについて解説していきます。
まずは基本をマスターしたい!という方は練習問題の方へ進んでください。
応用力もつけておきたい!という方は次の章でビシバシと鍛えていきましょう。
たすき掛けの因数分解【発展】
次の式を因数分解しなさい。
$$x^2+(y+4)x-(y-3)(2y+1)$$
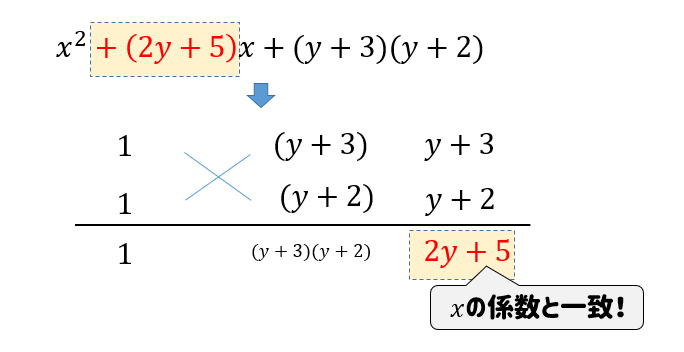
このような複雑な式であっても、\((y-3)\)と\((2y+1)\)をそれぞれのパーツとして見ることで

$$\begin{eqnarray}&&x^2+(y+4)x-(y-3)(2y+1)\\[5pt]&=&\{x-(y-3)\}\{x+(2y+1)\}\\[5pt]&=&\color{red}{(x-y+3)(x+2y+1)} \end{eqnarray}$$
たすき掛けを利用して因数分解してやることができるのです。
たすき掛けっていうのは式でもOKってわけですね。
次の式を因数分解しなさい。
$$x^2-xy-2y^2-x-7y-6$$
なにをどうやって…たすき掛けすればいいんだ…
この式には絶望したくなっちゃいますねw
こういった式の場合、まずは
次数の低い文字でまとめる
というのが突破口となります。
今回の式では、\(x,y\)ともに次数が2なので
どちらの文字に着目してもよいのですが、今回は\(x\)について着目し、まとめていきます。
$$\begin{eqnarray} &&x^2-xy-2y^2-x-7y-6\\[5pt]&=&x^2-(y+1)x-2y^2-7y-6\\[5pt]&=&x^2-(y+1)x-(2y^2+7y+6)\\[5pt]&=&x^2-(y+1)x-(2y+3)(y+2)\end{eqnarray}$$
すると、不思議なことにキレイにまとまっていくのです。
ここまでくれば、式のたすき掛けを利用して因数分解していけばOK!

$$\begin{eqnarray}&&x^2-(y+1)x-(2y+3)(y+2)\\[5pt]&=&\{x-(2y+3)\}\{x+(y+2)\}\\[5pt]&=&\color{red}{(x-2y-3)(x+y+2)} \end{eqnarray}$$
何をどうすれば…と、困った場合には
上の因数分解のように、まずは次数の低い文字でまとめる!
そうすれば何かしらの突破口が見えてきて、たすき掛けが利用できる形を導くことができたりしますよ(^^)
たすき掛けの因数分解【練習問題】
ここの章ではひたすら、たすき掛けの因数分解を練習して理解を深めていきましょう!
次の式を因数分解しなさい。
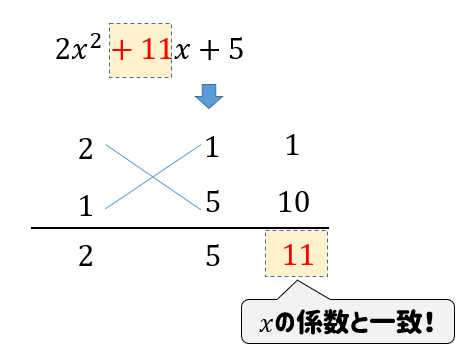
$$2x^2+11x+5$$
次の式を因数分解しなさい。
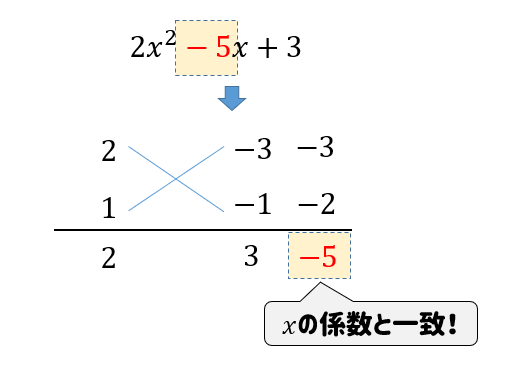
$$2x^2-5x+3$$
次の式を因数分解しなさい。
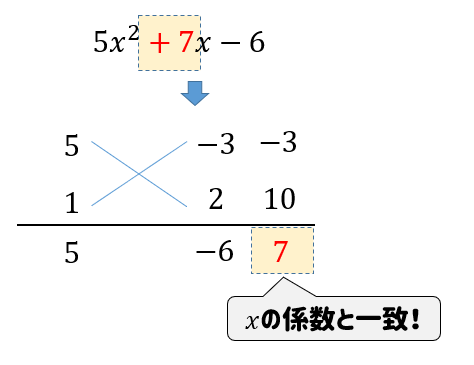
$$5x^2+7x-6$$
次の式を因数分解しなさい。
$$4x^2+4x-3$$
次の式を因数分解しなさい。
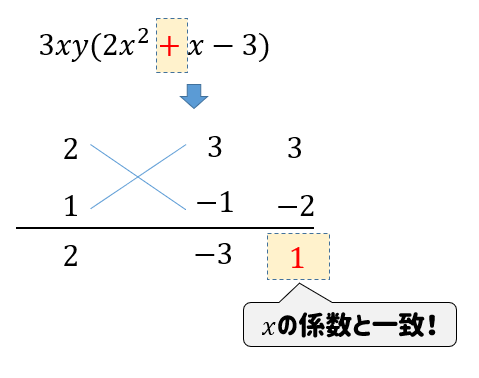
$$6x^2+7xy-3y^2$$
次の式を因数分解しなさい。
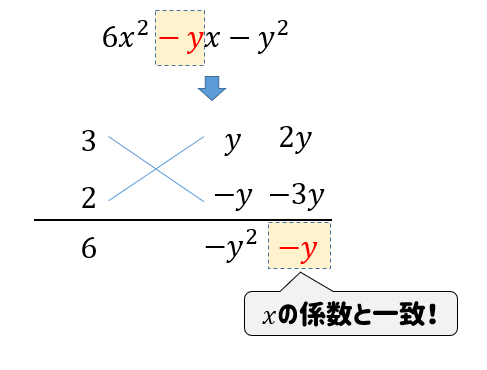
$$6x^2-xy-y^2$$
次の式を因数分解しなさい。
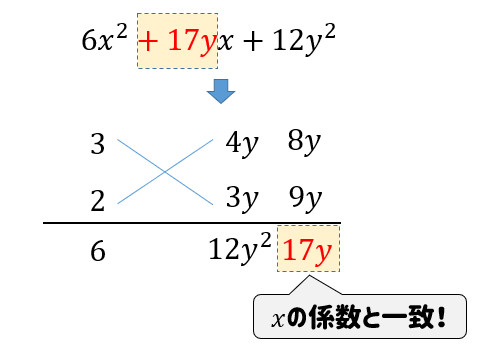
$$6x^2+17xy+12y^2$$
次の式を因数分解しなさい。
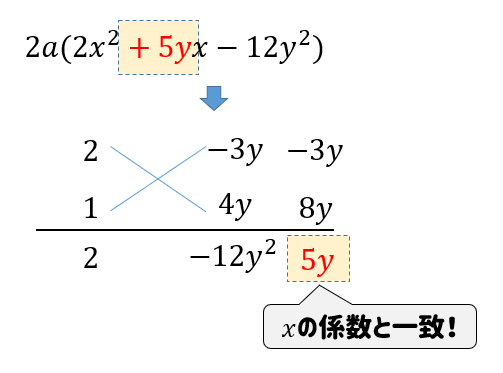
$$4ax^2+10axy-24ay^2$$
次の式を因数分解しなさい。
$$6x^2+10x+4$$
次の式を因数分解しなさい。
$$6x^3y+3x^2y-9xy$$
【発展】次の式を因数分解しなさい。
$$2x^2-(3y-1)x-(2y-1)(y-1)$$
【発展】次の式を因数分解しなさい。
$$x^2+2xy+y^2+5x+5y+6$$
たすき掛けの因数分解【まとめ!】
お疲れさまでした!
たすき掛けの因数分解はとにかく練習で慣れるのが一番!
たくさん練習した人は、わざわざたすき掛けを書かなくても
頭の中で因数分解ができるようになってくるぞ(/・ω・)/
たすき掛けの基本はバッチリ!という方は
勇気を出して発展にも挑戦してみましょう。
思っていたよりも難しくないぞ!ってことに気がつくはずだ(^^)




















わかりやすい
練習の問題数が多くてとても助かりました!
ありがとうございます!
これで定期テスト乗り切ります!
それはよかったです^^
テスト結果がよかったら嬉しいな!
とてもためになる
時間がかかっちゃって、めんどい〜
慣れが大切ですね(^^;
たっくさん練習しましょう!!