高校数学Ⅰで学習する不等式の単元から
「連立不等式の整数解」
についての問題を解説します。
連立不等式の整数解とは、次のような問題のことをいいます。
【問題】ニューアクションβより
\(a\)を定数とする。2つの不等式
\(2(3x-4)-1>-3(2x+11)\cdots ①\)
\(4x+2a<3x+2\cdots ②\)
をともに満たす整数\(x\)がちょうど3個となるような\(a\)の値を求めよ。
よく聞かれる質問として、
答えの範囲に<、≦のどちらを選べばいいか分かりません…
というものがあります。
というわけですので、
この点について詳しく解説していきますね!
今回の内容をサクッと学びたい方は、こちらの動画をチェック!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
連立不等式の整数解の問題解説!
【問題】ニューアクションβより
\(a\)を定数とする。2つの不等式
\(2(3x-4)-1>-3(2x+11)\cdots ①\)
\(4x+2a<3x+2\cdots ②\)
をともに満たす整数\(x\)がちょうど3個となるような\(a\)の値を求めよ。
まずは、①②それぞれの不等式を解きましょう。
①より
$$\begin{eqnarray}2(3x-4)-1&>&-3(2x+11)\\[5pt]6x-8-1&>&-6x-33\\[5pt]12x&>&-24\\[5pt]x&>&-2 \end{eqnarray}$$
②より
$$\begin{eqnarray}4x+2a&<&3x+2\\[5pt]x&<&2-2a \end{eqnarray}$$
となります。
そして、これらの範囲を同時に満たす\(x\)が存在するとき
\(x\)の値の範囲は、\(-2<x<2-2a\) となるはずです。
\(2-2a\)の値が具体的には分かりませんが、
今のところ\(-2\) より大きくないといけないってことは分かりますよね。
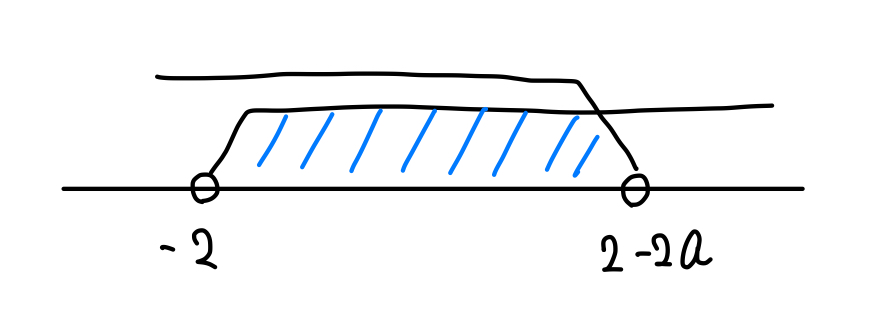
次に、問題で与えられているように
\(-2<x<2-2a\)の中に整数がちょうど3個だけ入るように考えていきます。
範囲の左端が\(-2\)であることから、整数を3個入れるためには次のようになります。
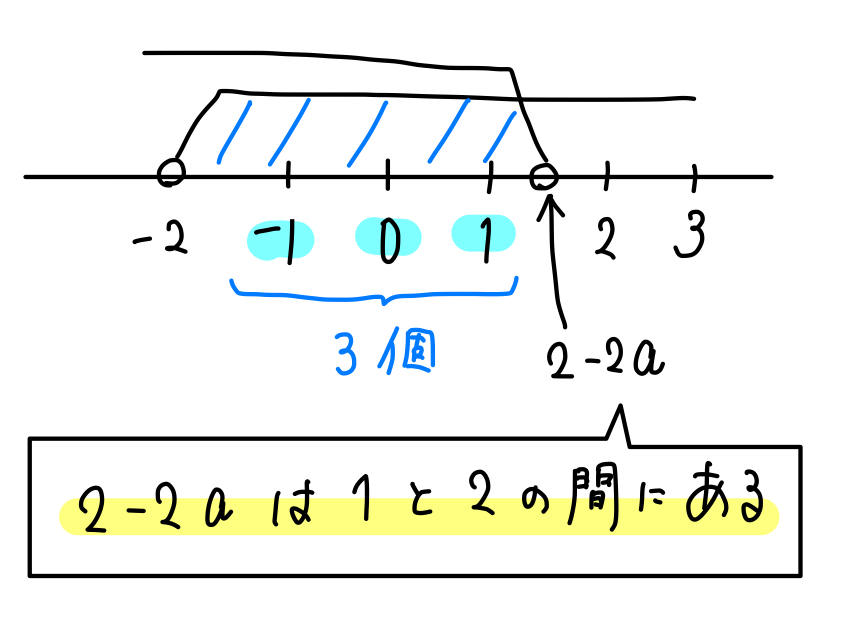
ここで、\(2-2a\) の場所が具体的に判明します。
次に\(2-2a\) をもっと細かく絞っていきます。
1と2の間にあることは分かりましたが、
1と2に等しくなる場合はどうなのか?
をチェックしていきましょう。
\(2-2a\) が1と等しくなる場合、範囲は次のようになってしまいます。
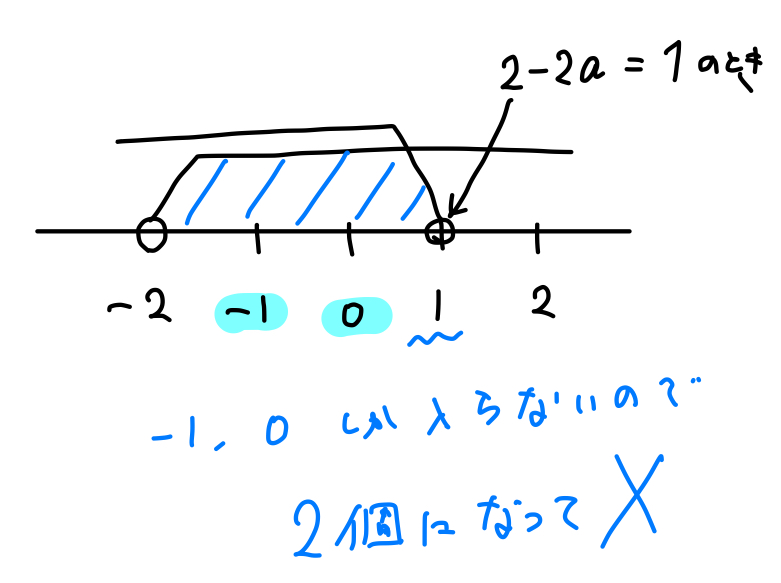
これだと範囲の中に入っている整数が\(-1,0\)の2個だけになってしまい、問題の条件を満たさなくなってしまいます。
このことから、\(2-2a\)は1にはならない。ということが分かります。
次に、\(2-2a\) が2と等しくなる場合、範囲は次のようになります。
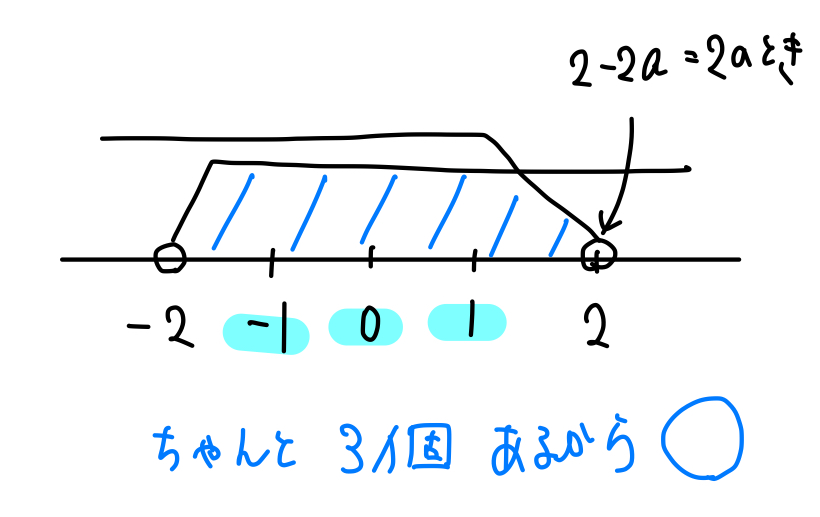
こちらはちゃんと範囲の中に整数が3個入っていて、問題の条件を満たしていますね。
このことから、\(2-2a\)は2でもOK!ということが分かります。
以上のことをまとめると、
①②を満たす整数\(x\)がちょうど3個となるようにするためには、
\(2-2a\)が1と2の間にくる必要がある。
だけど、\(2-2a\)が1になってしまうとダメ、2のときはOK。
⇒ \(1<2-2a≦2\)
このように、\(a\)に関する不等式を作ることができました。
あとはこれを解いていけばOKです。
$$\begin{eqnarray}&&1<2-2a≦2\\[5pt]&&-1<-2a≦0\\[5pt]&&0≦a<\frac{1}{2}\cdots(解) \end{eqnarray}$$
いかがだったでしょうか。
答えの範囲に=がつく、つかないの理由が分かりましたか?
=にしたときにちゃんと条件を満たすかどうか。
これをチェックしていけば、間違いなく判断ができるはずですよ(^^)
- それぞれの不等式を解く。
- \(a\)を含む値がどこの間にくればよいかを考える。
- ②で求めた範囲の両端でも成り立つか調べる。
- ②③を元に不等式を作る。
では、練習問題に挑戦して理解を深めておきましょう!
練習問題に挑戦!
【問題】
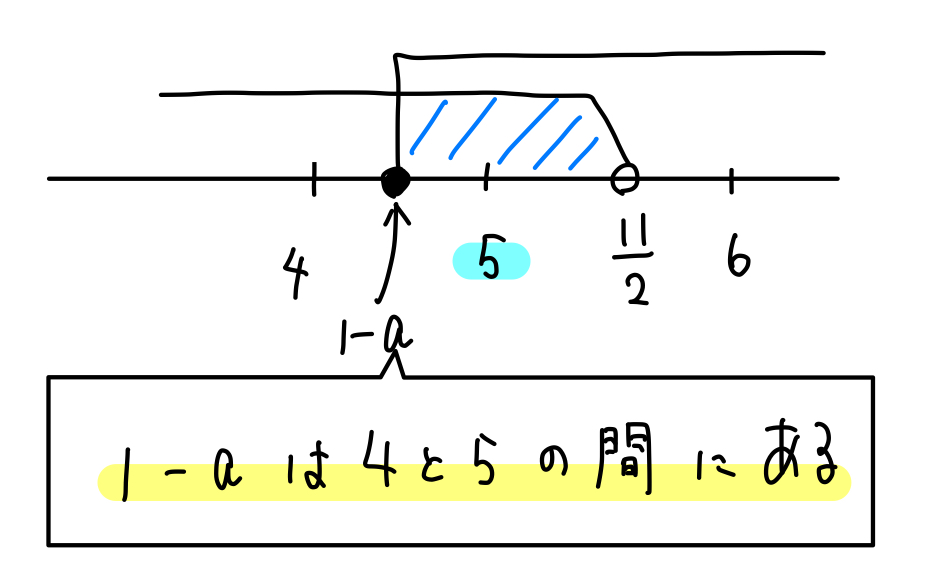
連立不等式 \(x-6<5-x\cdots①\), \(5x+1≦6x+a\cdots ②\) を満たす\(x\)の整数値が5のみとなるように、\(a\)の値の範囲を求めよ。
まとめ!
お疲れ様でした!
これで連立不等式の整数解についてはバッチリかな?
この問題は模試や入試で出題されやすい問題だから
確実に点が取れるようしておくと、偏差値も上がりやすくなるね(/・ω・)/
他の不等式問題については、こちらの記事も参考にしてみてね!



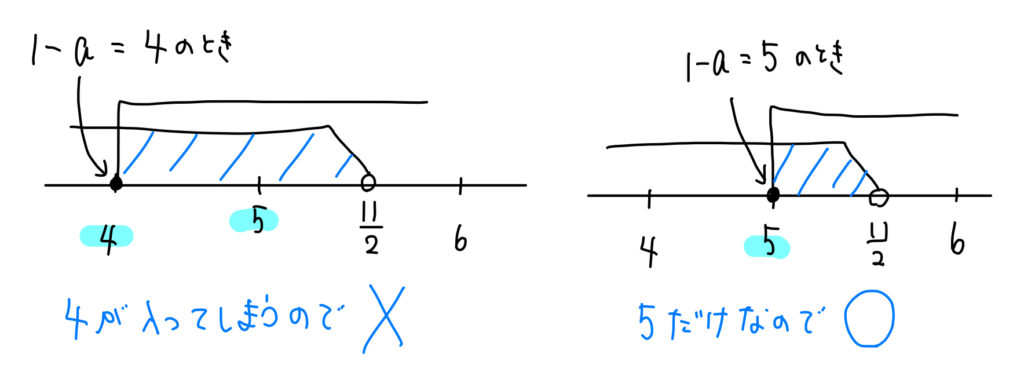














コメントを残す