対称式の変形まとめ！基本公式を覚えてサクサク計算しよう！

今回は数学Ⅰで学習する単元から

「対称式の変形、基本公式」

について、まとめていきます。

対称式というのは、

$x^2+y^2$、$x^3+y^3$、$x+\frac{1}{x}$

といった、2つの文字を入れかえても元の式と同じになる式のことをいいます。

高校数学Ⅰの問題では、対称式を用いて式の値を求めなさい。

というような問題がよく出題されます。

このときに、対称式の変形（基本公式）を覚えておくとラクに計算ができるようになります。

では、対称式の変形を導く方法などを解説。

そして、練習問題に取り組んでみましょう！

対称式の基本については、こちらの動画でも解説しています。

まずは2乗、３乗の変形をおさえておくことが大事ですね＾＾

Contents

対称式の変形
- 対称式の基本変形を確認！
- 対称式の分数変形を確認！
対称式の値を求める問題に挑戦！
まとめ！
がんばっているのに60点の壁をクリアできない中3生の方へ
- こちらの関連記事はいかがでしょうか？

対称式の変形

対称式の基本変形を確認！

$x^2+y^2$、$x^3+y^3$については、

めちゃくちゃ出題されます！

なので、丸暗記しておいた方がラクですね。

以下にそれぞれの変形方法について紹介しておきますので、参考にしておいてください！

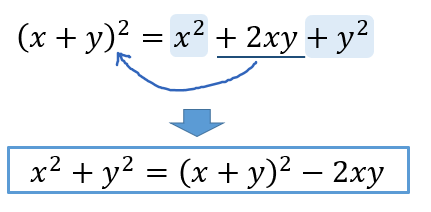
二乗の展開公式を使って、$2xy$を移項してやれば、

$x^2+y^2$の変形が完了です！簡単ですね(^^)

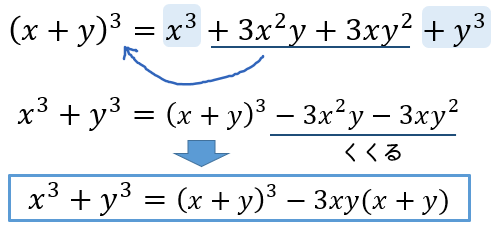
3乗の展開公式を使って、$3x^2y$と$3xy^2$を移項します。

そして、この2つの項を共通因数でくくってやれば完成です！

この変形を覚えてるためには、3乗の展開公式をマスターしておく必要があります。

>【三乗の展開公式】(a+b)3乗の計算方法は？問題を使って解説！

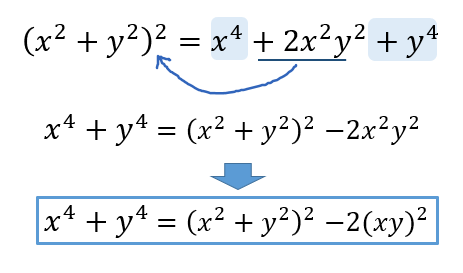
4乗の変形をするために、4乗の展開を…！

としてしまうと、計算に困ってしまいます(^^;)

なので、4乗を作るためには$(x^2+y^2)^2$を考えるというのが大事なポイントです。

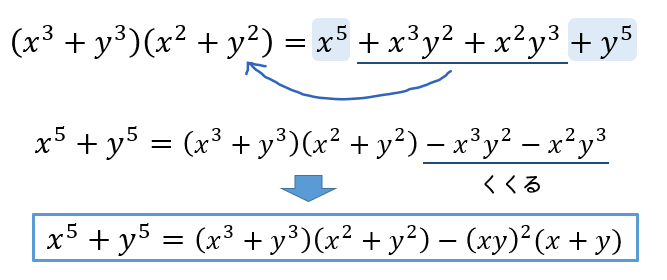
5乗の変形をするためには、

$(x^3+y^3)$と$(x^2+y^2)$の積を考えていきましょう。

ここも5乗の展開を…としてしまうと苦しいことになってしまうので注意です(^^;)

対称式の分数変形を確認！

分数の変形については、出題頻度が低いことや変形の見た目がゴチャッとしていることから、丸暗記ではなく自分で導けるようにしておくのがおススメです。

というわけで、分数パターンについても変形を確認しておきましょう。

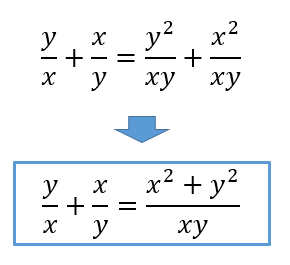
分母が$xy$になるよう通分して、まとめていけばOKです。

分子の$x^2+y^2$については、もっと細かく変形して

$$\frac{y}{x}+\frac{x}{y}=\frac{(x+y)^2-2xy}{xy}$$

とすることもできます。

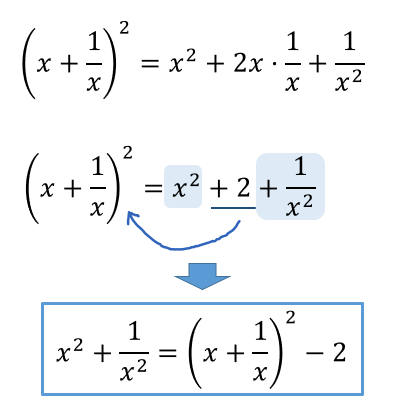
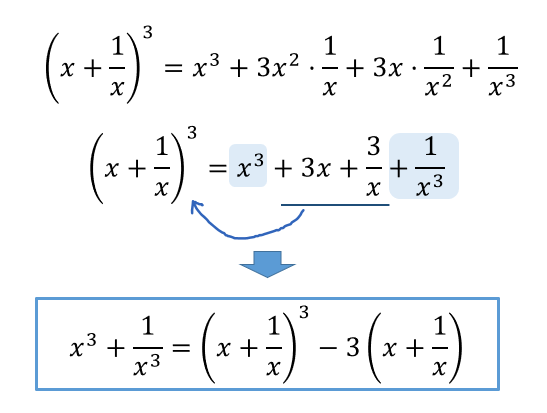
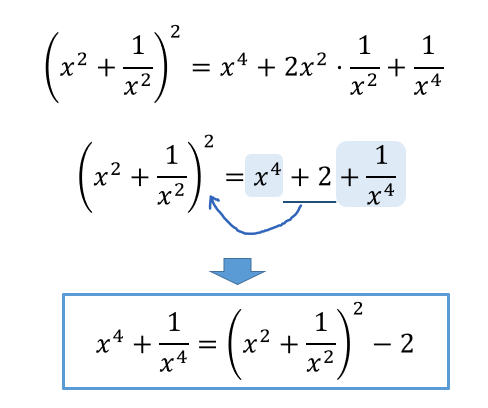
展開公式を利用すると、約分されて数だけになってしまう項があるよね！

そこんとこの計算をミスしないように気を付けてください。

対称式の値を求める問題に挑戦！

【問題】

$x+y=4$,$xy=1$ のとき、次の式の値を求めなさい。

（1）$x^2+y^2$

（2）$x^3+y^3$

（3）$x^4+y^4$

（4）$x^5+y^5$

解説＆答えはこちら

【答え】

（1）$14$ （2）$52$ （3）$194$ （4）$724$

（1）

$$\begin{eqnarray}x^2+y^2&=&(x+y)^2-2xy\\[5pt]&=&4^2-2\cdot 1\\[5pt]&=&14 \end{eqnarray}$$

（2）

$$\begin{eqnarray}x^3+y^3&=&(x+y)^3-3xy(x+y)\\[5pt]&=&4^3-3\cdot 1\cdot 4\\[5pt]&=&52 \end{eqnarray}$$

（3）

$$\begin{eqnarray}x^4+y^4&=&(x^2+y^2)^2-2(xy)^2\\[5pt]&=&14^2-2\cdot 1^2\\[5pt]&=&194 \end{eqnarray}$$

（4）

$$\begin{eqnarray}x^5+y^5&=&(x^3+y^3)(x^2+y^2)-(xy)^2(x+y)\\[5pt]&=&52\cdot 14-1^2\cdot 4\\[5pt]&=&724 \end{eqnarray}$$

【問題】

$x=\sqrt{2}-1$ のとき、次の式の値を求めなさい。

（1）$x+\frac{1}{x}$

（2）$x^2+\frac{1}{x^2}$

（3）$x^3+\frac{1}{x^3}$

解説＆答えはこちら

【答え】

（1）$2\sqrt{2}$ （2）$6$ （3）$10\sqrt{2}$

（1）

$$\begin{eqnarray}x+\frac{1}{x}&=&(\sqrt{2}-1)+\frac{1}{\sqrt{2}-1}\\[5pt]&=&\sqrt{2}-1+(\sqrt{2}+1)\\[5pt]&=&2\sqrt{2} \end{eqnarray}$$

（2）

$$\begin{eqnarray}x^2+\frac{1}{x^2}&=&\left(x+\frac{1}{x}\right)^2-2\\[5pt]&=&(2\sqrt{2})^2-2\\[5pt]&=&6 \end{eqnarray}$$

（3）

$$\begin{eqnarray}x^3+\frac{1}{x^3}&=&\left(x+\frac{1}{x} \right)^3-3\left(x+\frac{1}{x} \right)\\[5pt]&=&(2\sqrt{2})^3-3\cdot 2\sqrt{2}\\[5pt]&=&16\sqrt{2}-6\sqrt{2}\\[5pt]&=&10\sqrt{2} \end{eqnarray}$$

まとめ！

以上、対称式の変形についてでした。

これらの変形は模試、入試などでは頻繁に利用されます。

なので、たくさん問題を解きながら式変形を覚えておきましょう！

こちらの記事も合わせてどうぞ！

がんばっているのに60点の壁をクリアできない中3生の方へ

頑張っているのに思うように成績が上がらず、
「このままだと本番で数学60点が厳しいかも…」
と不安に感じているあなた。

もしかして、
このような問題に直面していませんか？

模試になると点がガクッと落ちる
復習のやり方が分からない
勉強してもすぐに忘れる
凡ミスが直らない
家だと集中して勉強できない
問題集を買っても、1人で解けなくて途中でやめてしまう
友人が点を伸ばしていて焦る
頑張りたいから何をすればいいか教えて欲しい

僕が2年前に指導させてもらった中3のAくん
彼がまさにこのような状態でした。

すごく勉強したのに試験の結果が36点…

「どうすればいいか分からない…」
「点を上げれる自信がない…」

自信をなくし落ち込んでいましたが、
ある勉強方法を取り入れたことによって
Aくんは大変身！

なんと、たった2ヶ月で
36点　⇒　72点
なんと、驚きの36点UPを達成！

何をやっても点が伸びなかったAくん
彼を大変身させた「ある勉強方法」とは、
たったの3分で取り組める簡単なものです。

この勉強法を活用した人は、

43点　⇒　69点

67点　⇒　94点

人生初の100点！

このように次々と良い結果を報告してくれています＾＾

Aくんを大変身させた「ある勉強法」を
あなたにも活用してもらい
今すぐにでも結果を出して欲しいです。

そこで！
ある勉強法を正しく身につけてもらうための
1週間の集中メルマガ講座を作成しました。

こちらのメルマガ講座の中で、
順にワークをお渡ししていくので1つずつ取り組み、
やればやっただけ点が伸びていく感覚を掴んでくださいね！

もちろんこの講座の登録は無料！
いますぐワークを受け取っておきましょう('◇')ゞ

無料でワークをもらう！

数スタの他記事はこちらから