高校数学Ⅰで学習する因数分解の単元から
「3次式の因数分解のやり方」
について解説していきます。
3次式の因数分解の公式は次の通りです。

今回の記事はこちらの動画でも解説しています(/・ω・)/
また、高校数学Ⅱの問題集に載っているこちらの問題についても解説を用意しました。
【練習問題】次の式を因数分解しなさい。
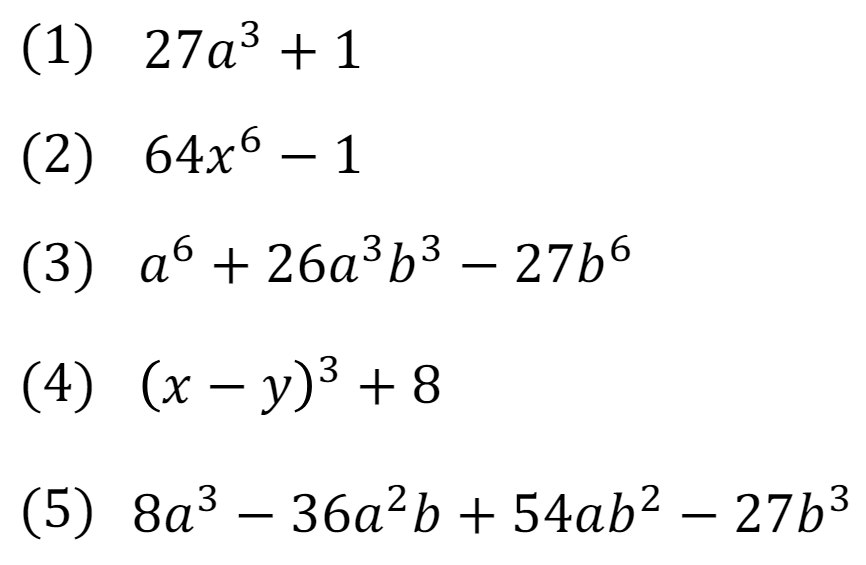
解説は記事の後半で!
まずは公式の活用について確認していきましょう。
3次の因数分解公式とやり方について
公式①
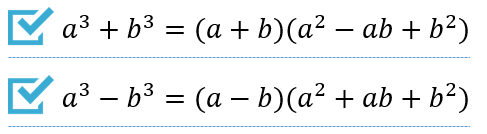
一番使用頻度が高いのがこの公式です。
例題を見ながら公式の使い方を確認しておきましょう。
【例題】
次の式を因数分解せよ。
$$8x^3-27$$
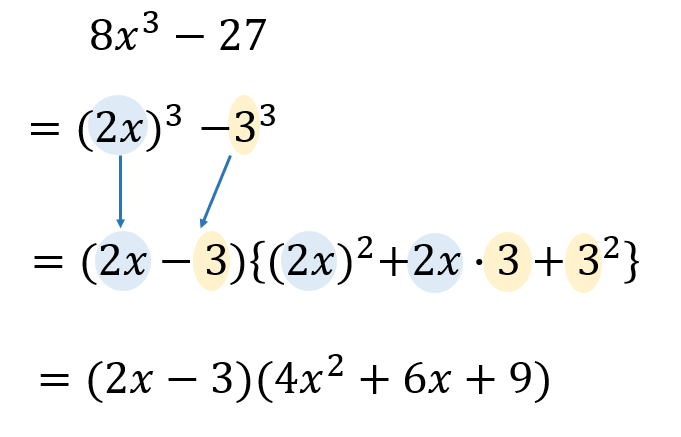
式を見たときに、(三乗)+(三乗)、(三乗)-(三乗)の形になっていれば、この公式を使うことができます。
ここでは、どんな数が3乗の形になるのかを判断できるようにしておく必要があります。
よく出てくる3乗の形は以下の通りです。これらは頭に入れておきましょう。
$$8=2^3$$
$$27=3^3$$
$$64=4^3$$
$$125=5^3$$
$$216=6^3$$
公式②
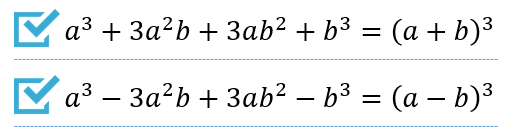
こちらは使用頻度が低めですが、いざというときに覚えておきたい公式です。
まぁ、3乗の展開公式は覚えてもらったと思うので、それの逆だと考えればすぐに思い出せますね。
>【三乗の展開公式】(a+b)3乗の計算方法は?問題を使って解説!
【例題】
次の式を因数分解しなさい。
$$x^3+12x^2+48x+64$$
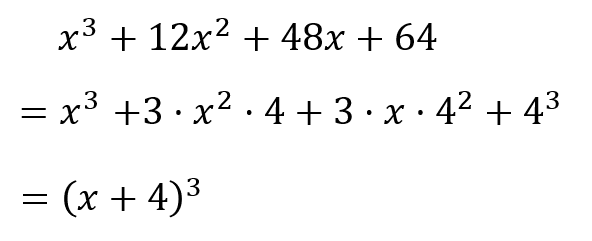
公式の使い方は分かったけど、
パッと式を見たときに、
この公式を利用するってことが思いつかない!
という声が聞こえてきそうです(^^;)
確かに、パッと見では判断が難しいのですが、
文字に着目したときに、3乗⇒2乗⇒1乗⇒定数項
のような並びになっているときには、今回の3乗公式が使えるかも!
と覚えておいてください。
まぁ、使用頻度は少ないので
あまり活躍することはないのですが(^^;)
公式③
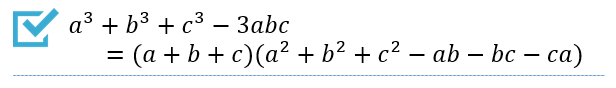
これまた使用頻度が低い公式なのですが、
これを知っておくと1ランク上の問題を解くことができるようになります。
ちなみに、今回は因数分解の公式として紹介していますが、
展開公式として逆の計算をするときにも活用することがあります。
公式を覚えておかないと以下のように置き換えを利用して解く必要があります。
(まぁ使用頻度が低いので覚えるのが大変なら置き換えでやる方がよいですが)
$$\begin{eqnarray}&&a^3+b^3+c^3-3abc\\[5pt]&=&(a+b)^3-3ab(a+b)+c^3-3abc\\[5pt]&=&\{(a+b)^3+c^3\}-3ab(a+b+c)\\[5pt]&=&\{(a+b)+c\}\{(a+b)^2-(a+b)c+c^2\}-3ab(a+b+c)\\[5pt]&=&(a+b+c)(a^2+2ab+b^2-ac-bc+c^2-3ab)\\[5pt]&=&(a+b+c)(a^2+b^2+c^2-ab-bc-ca) \cdots(解)\end{eqnarray}$$
因数分解の途中で、3乗の対称式を利用しています。
$$a^3+b^3=(a+b)^3-3ab(a+b)$$
対称式については、こちらの記事もご参考くださいね!
では、例題を使って公式を用いた因数分解についても確認しておきましょう。
【例題】
次の式を因数分解せよ。
$$x^3+y^3-3xy+1$$
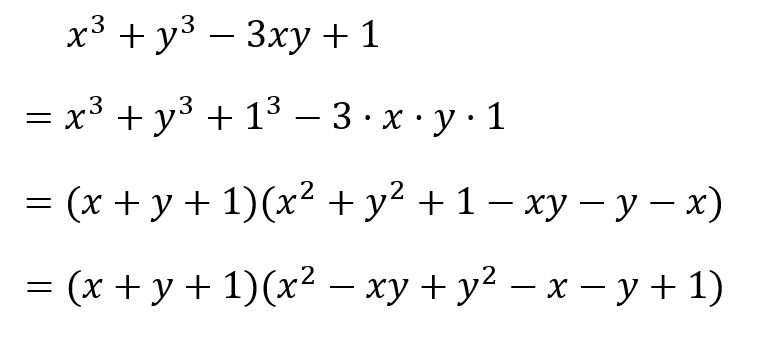
練習問題の解説
【練習問題】次の式を因数分解しなさい。
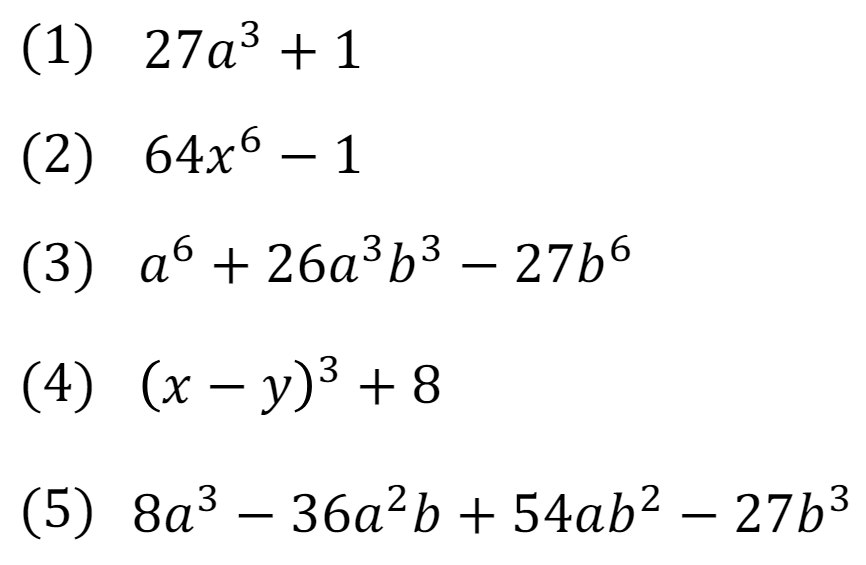
サクッと理解したい方はこちらの解説動画をどうぞ!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
(1)基本
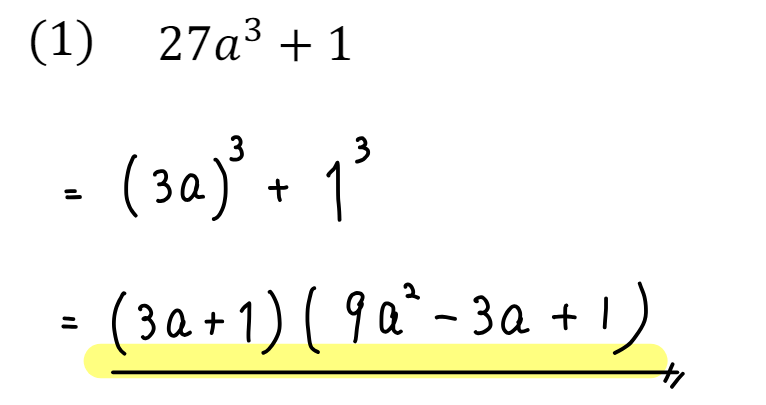
3乗+3乗の形になっているので、そのまま公式に当てはめればOKですね!
(2)2乗の形を作るのがポイント
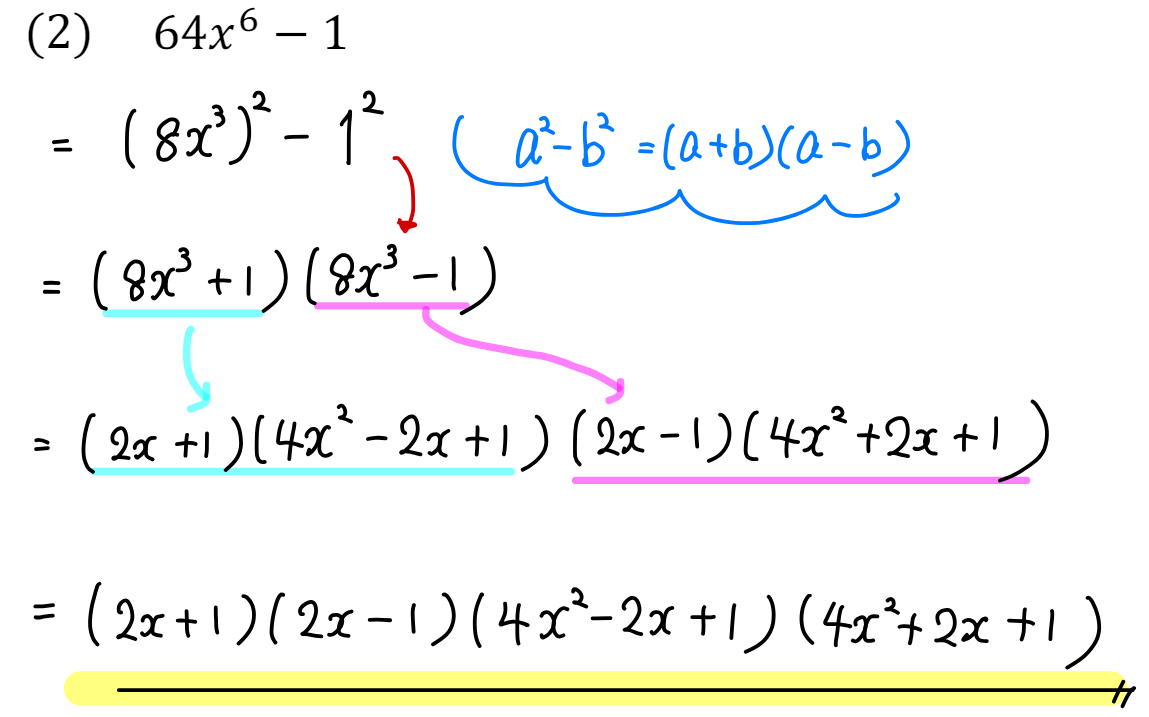
これはなかなか難しい1問でした(^^;
\(64x^6-1=(4x^2)^3-1^3=(8x^3)^2-1^2\)
このように「3乗-3乗」「2乗-2乗」どちらの形も作れるのですが、3乗-3乗の形からスタートしてしまうと途中の計算が難しくなり困ってしまいます…
なので、上の解答にあるように2乗-2乗の形から因数分解をスタートしていくとよいです。
ちなみに、3乗-3乗でスタートした場合の計算についてはこちらの動画で解説しているので、気になる方は参考にしてみてください。(8分あたりから)
(3)同じパーツを作って置き換え
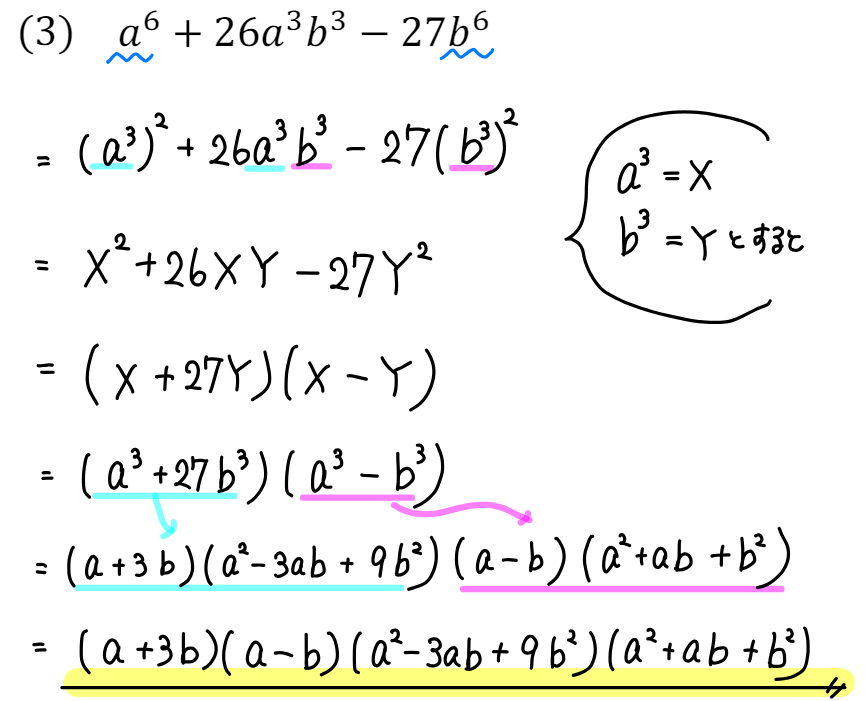
\(a^6=(a^3)^2\)という変形が作れるかどうかがポイントですね!
3乗の練習をやっているところなので、\(a^6=(a^2)^3\) としたくなるところですが…グッとこらえてください!
(4)かたまりをつかって
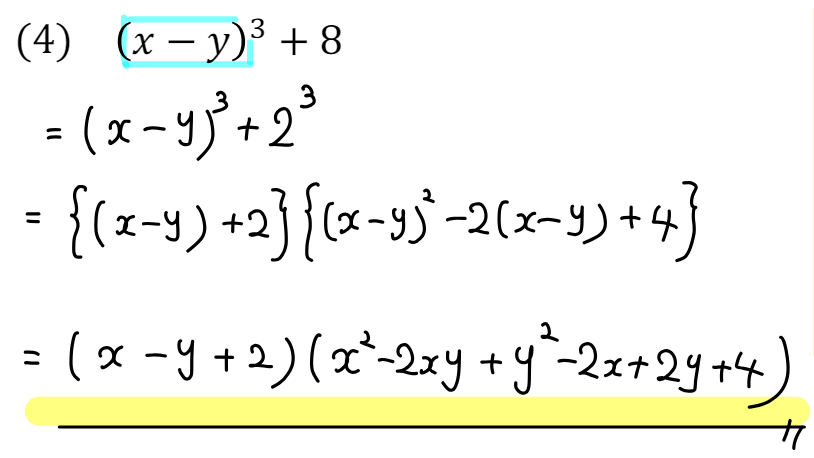
\((x-y)\)をひとかたまりと考えて、そのまま公式に当てはめていけばいいですね^^
(5)3乗のペアを見つけよう
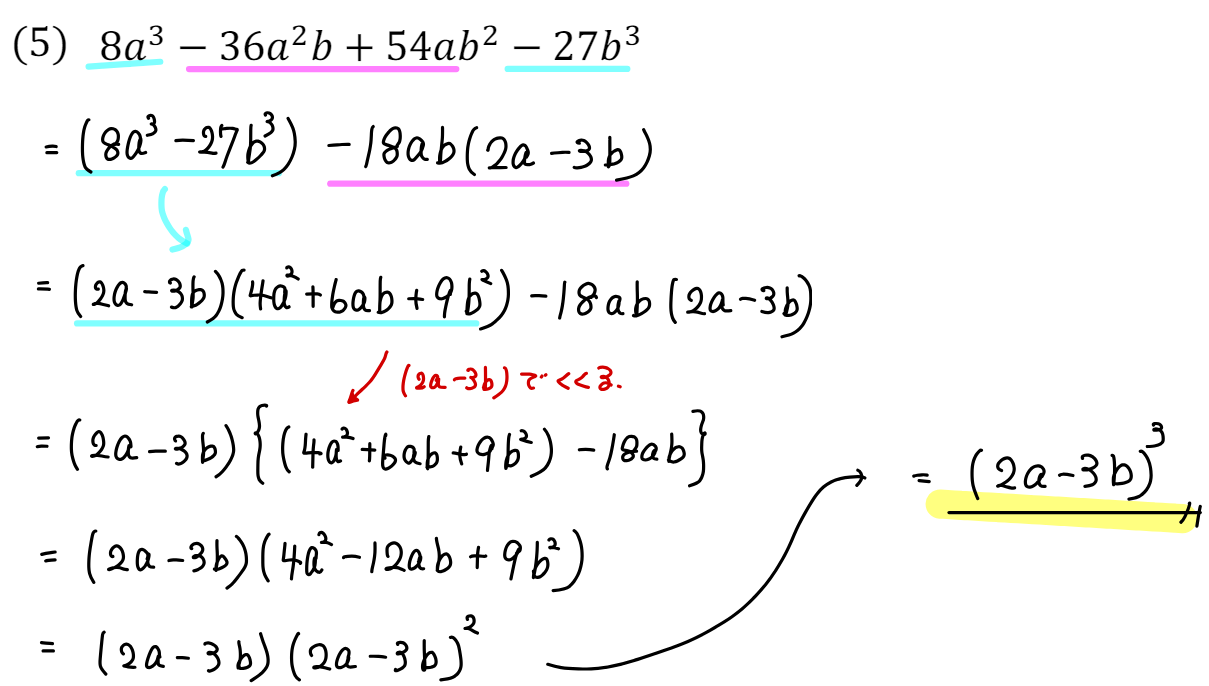
最初に3乗のペアを見つけて分類していきましょう。
そうすればあとは流れで進めていけるはずです^^
まとめ!
最後に3乗の因数分解公式をまとめておきましょう。

上2つの公式については、めちゃくちゃ使います。
なので、問題を解いていく中で自然と覚えれるのですが、
下の3つの公式に関しては使うことも少ないので、
なかなか覚えれない…という人も多いかと思います。
なので、上の公式画像をスマホに保存しておいて、
大事な試験の前に軽く見直せるようにしておきましょう!

















コメントを残す