4乗！？複二次式の因数分解の解き方！途中式をていねいに解説するぞ！

こんにちは！数スタの小田です。

今回は数学Ⅰで学習する因数分解の単元から

「複二次式の因数分解」

について取り上げていきます。

複二次式とは、\(ax^4+bx^2+c\) のような形になっている式のことをいいます。

そして、この複二次式を因数分解する場合

大きく分けて解き方は2通りあります。

今回の内容をサクッと理解したい方は、こちらの動画がおススメです！

（1）の解説！置き換えを利用して2次式にする。

複二次式の因数分解では、まず置き換えを考えてみましょう。

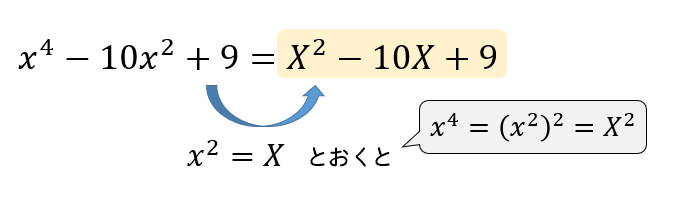
このように、\(x^2=X\)とおくことにより、見慣れた形の二次式にすることができました。

$$\begin{eqnarray}&&x^4-10x^2+9\\[5pt]&=&X^2-10X+9\\[5pt]&=&(X-9)(X-1)\\[5pt]&=&(x^2-9)(x^2-1)\\[5pt]&=&(x+1)(x-1)(x+3)(x-3)\cdots(解) \end{eqnarray}$$

複二次式では、まず\(x^2=X\)とおいて二次式に変換することを考えてみましょう。

二次式に変換したとき、そこから因数分解ができるようであればそのまま進めていけばOK。

置き換えをしたのに因数分解ができない！？

という場合には、次で紹介する（2）のやり方をやっていきましょう。

（2）の解説！平方の差をつくる。

今回の問題では、（1）のように置き換えを利用すると

\(x^4-7x^2+1=X^2-7X+1\) となり、

…因数分解できないけど！！

と、困ったことになってしまいます(^^;)

こういう場合には、平方の差を作って因数分解を進めていきます。

平方の差とは、次のような形のことをいいます。

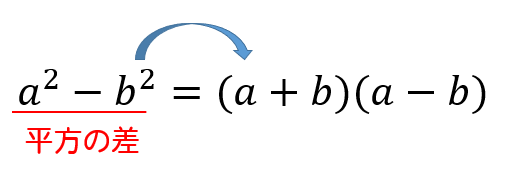
二乗ひく二乗の形を作ることができれば、上のように因数分解ができるようになりますね。

ということで、

置き換えを利用しても因数分解ができない複二次式については、

なんとか式変形をしながら、平方の差を作ることを考えていきます。

ここの式変形が慣れるまでは、ちょい難しいので

よく見ておいてくださいね！

まずは、\(x^4\)と\(1\)に注目をします。

$$\begin{eqnarray}x^4-7x^2+1=\color{red}{x^4+1}-7x^2 \end{eqnarray}$$

そして、\(x^4+1\)の部分が\((    )^2\)の形になるためには、どんなパーツが必要になるかを考えます。

すると、\(+2x^2\) または \(-2x^2\) であることが分かります。

これらのパーツを式の中に組み込んだとき、平方の差ができるのは\(+2x^2\)だと分かりますね。

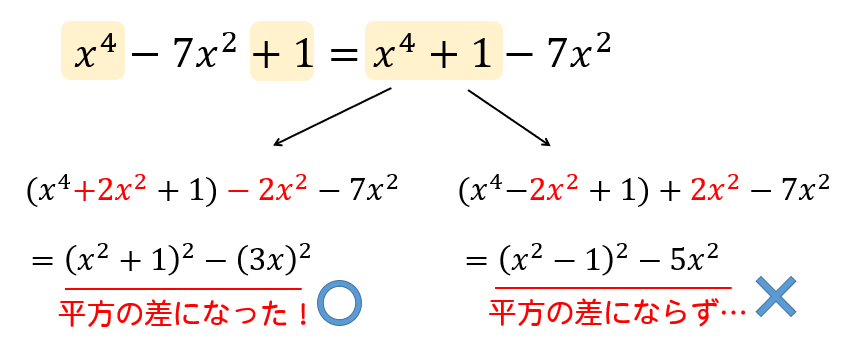
このように、平方の差になるパターンを見つけることができれば、あとは因数分解を進めていくだけです。

$$\begin{eqnarray}&&x^4-7x^2+1\\[5pt]&=&(x^4+2x^2+1)-9x^2\\[5pt]&=&(x^2+1)^2-(3x)^2\\[5pt]&=&\{(x^2+1)+3x\}\{(x^2+1)-3x\}\\[5pt]&=&(x^2+3x+1)(x^2-3x+1)\cdots(解) \end{eqnarray}$$

平方の差を作る変形は理解してもらえたかな？？

この変形については、たくさんの問題を解いて慣れていくといいよ！

記事下に練習問題を入れているので、そこで練習しておこうね！

（3）の解説！迷わず平方の差！

こちらの問題も（2）と同じく平方の差を利用していきます。

平方の差ができるパターンを見つけて因数分解を進めていきましょう。

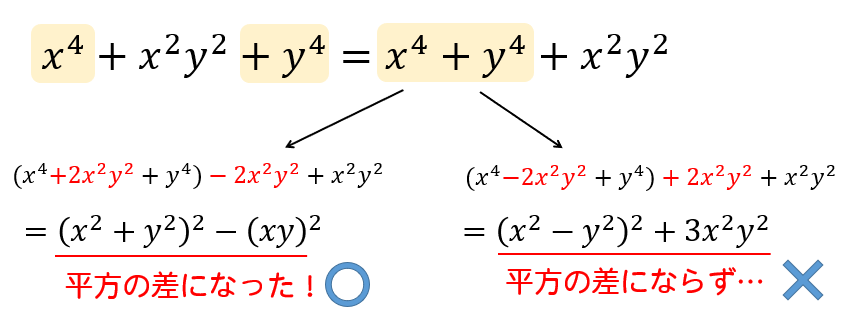
$$\begin{eqnarray}&&x^4+x^2y^2+y^4\\[5pt]&=&(x^4+2x^2y^2+y^4)-2x^2y^2+x^2y^2\\[5pt]&=&(x^2+y^2)^2-(xy)^2\\[5pt]&=&\{(x^2+y^2)+xy\}\{(x^2+y^2)-xy\}\\[5pt]&=&(x^2+xy+y^2)(x^2-xy+y^2)\cdots(解) \end{eqnarray}$$

複二次式の因数分解【練習問題】

まとめ！

お疲れ様でした！

複二次式の因数分解では、まず置き換えを考えてみること。

置き換えを利用しても因数分解がムリであれば平方の差を作る。

ということでした。

平方の差を作る式変形については、

今回の記事を通して、しっかりと身につけておいてくださいね！

高校数学で学習する因数分解は他にもたくさんあります。

⇒ 【まとめ】高校で学習する因数分解のやり方をぜんぶ解説！

こちらの記事でまとめているので参考にしてみてね(/・ω・)/